【内容速查与目录】

【笔记下载】

一、需求理论与供给理论

（一）需求理论

1. 需求量与需求定理

　　需求量：在给定价格水平下，愿意并能够购买的该商品数量。

　　需求定理：其他因素不变时，需求量随价格反方向变动。

2. 需求与影响因素

　　需求：消费者在一定时期内在各种可能的价格水平下愿意而且能够购买的该商品数量。==> 有效需求：有购买意愿且有支付能力

　　需求的影响因素：

该商品的价格
消费者收入
其他相关商品价格
消费者偏好
预期的未来价格

3. 需求函数与需求曲线

　　需求函数：\(Q_d=f(p_d,p_o,I,p_e,p_r)\)

　　\(p_d\)：该商品的价格

　　\(p_o\)：其他相关商品价格

　　\(I\)：消费者收入

　　\(p_e\)：消费者预期未来价格

　　\(p_r\)：消费者偏好

需求曲线

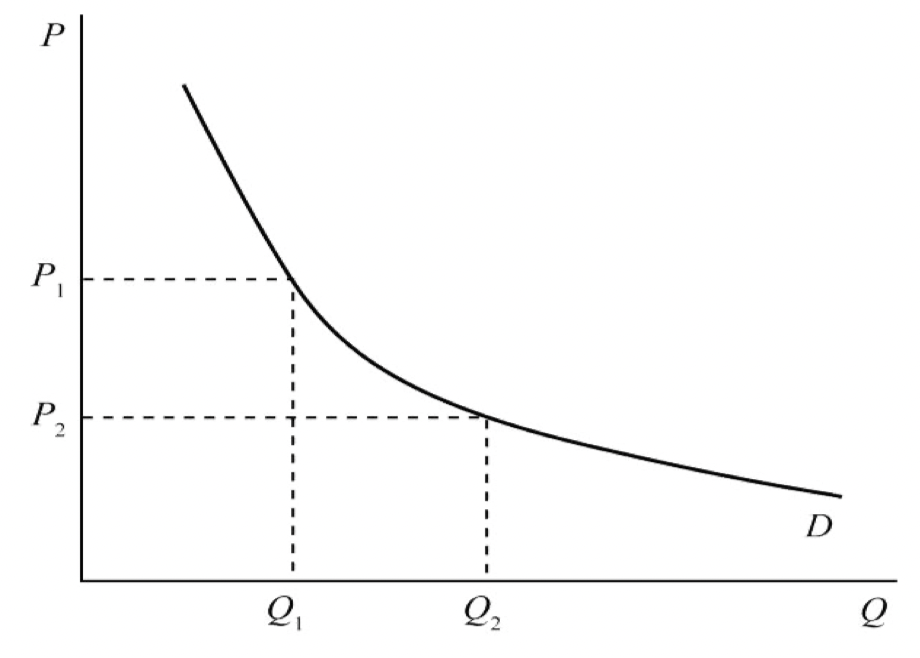
4. 需求/需求量的变动

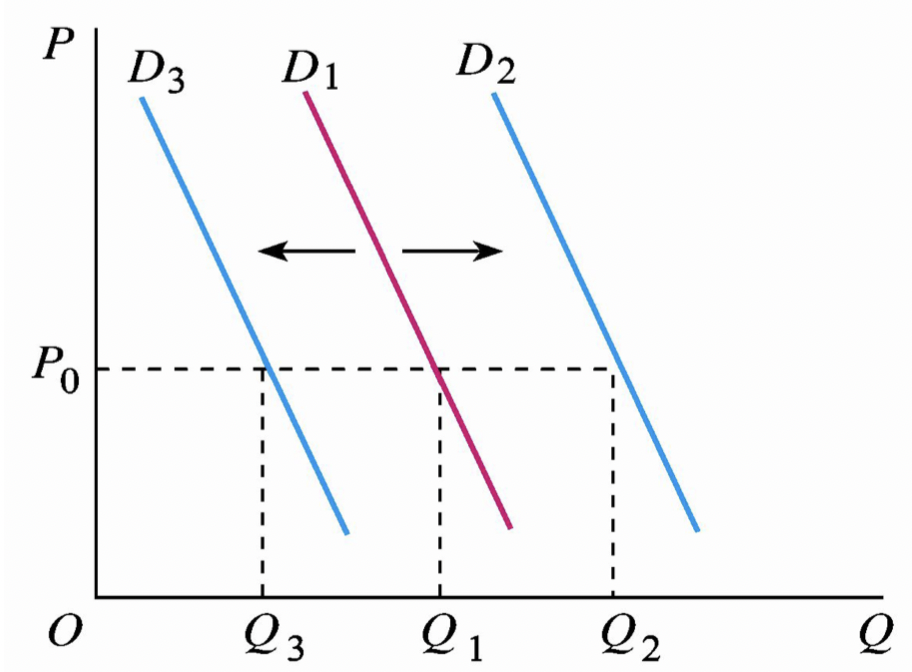
　　需求的变动：非价格因素（\(p_0,I,p_e,p_r\)）导致的变动，体现为需求曲线的水平移动，如 \(D_1\) 曲线移动至 \(D_2\) 或者 \(D_3\)。

需求的变动

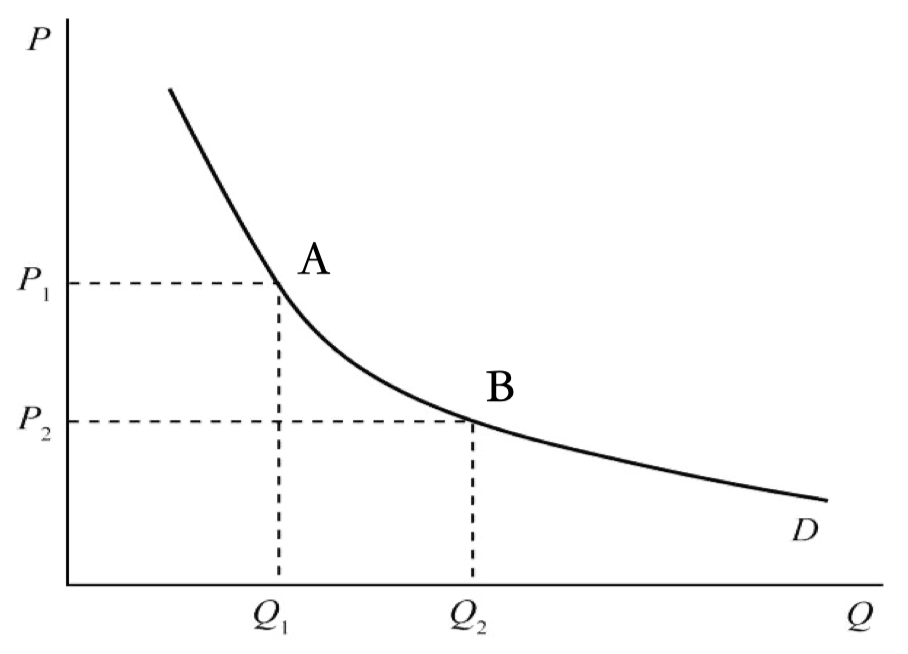
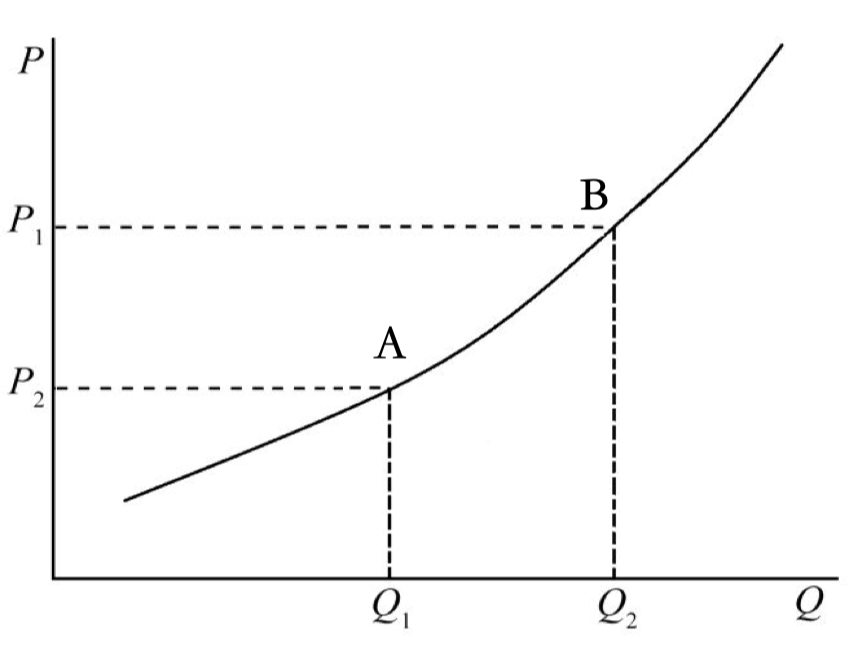
　　需求量的变动：该商品价格变化导致的变化，体现为点在需求曲线上的移动，即 \(Q_d=f(p_d)\)，如 \(A\) 点移动到 \(B\) 点。

需求量的变动

（二）供给理论

1. 供给量与供给定理

　　供给量：在给定价格水平下，愿意而且能够生产的产品数量。

　　供给定理：其他不变时，供给量随价格同方向变动。

2. 供给与影响因素

　　供给：生产者在一定时期内在各种可能的价格下愿意而且能够提供出售的该种商品数量。==> 有效供给：有生产欲望且有供给能力

　　供给的影响因素：

该商品的价格
生产成本
生产技术水平
其他相关商品价格
生产者对未来的预期

3. 供给函数与供给曲线

　　供给函数：\(Q_s=f(p_s,T,p_o,p_e,w,r,...)\)

　　\(p_s\)：该商品的价格

　　\(T\)：生产技术水平

　　\(p_o\)：其他相关商品价格

　　\(p_e\)：生产者预期未来价格

　　\(w\)：工人工资

　　\(r\)：利率

供给曲线

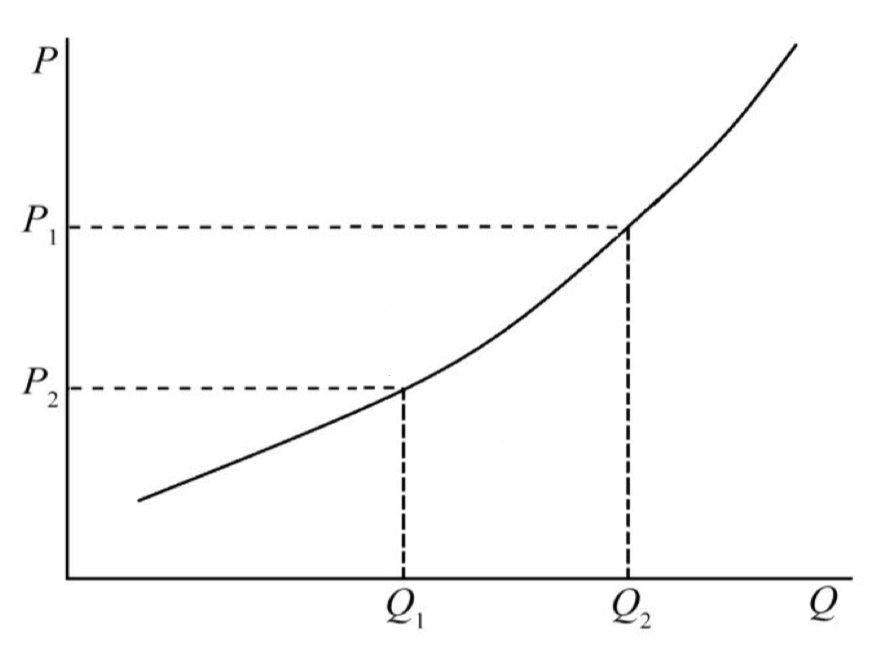
4. 供给/供给量的变动

　　供给的变动：非价格因素（\(T,p_o,p_e,w,r,...\)）导致的变动，体现为供给曲线的水平移动，如 \(S_1\) 曲线移动至 \(S_2\) 或者 \(S_3\)。

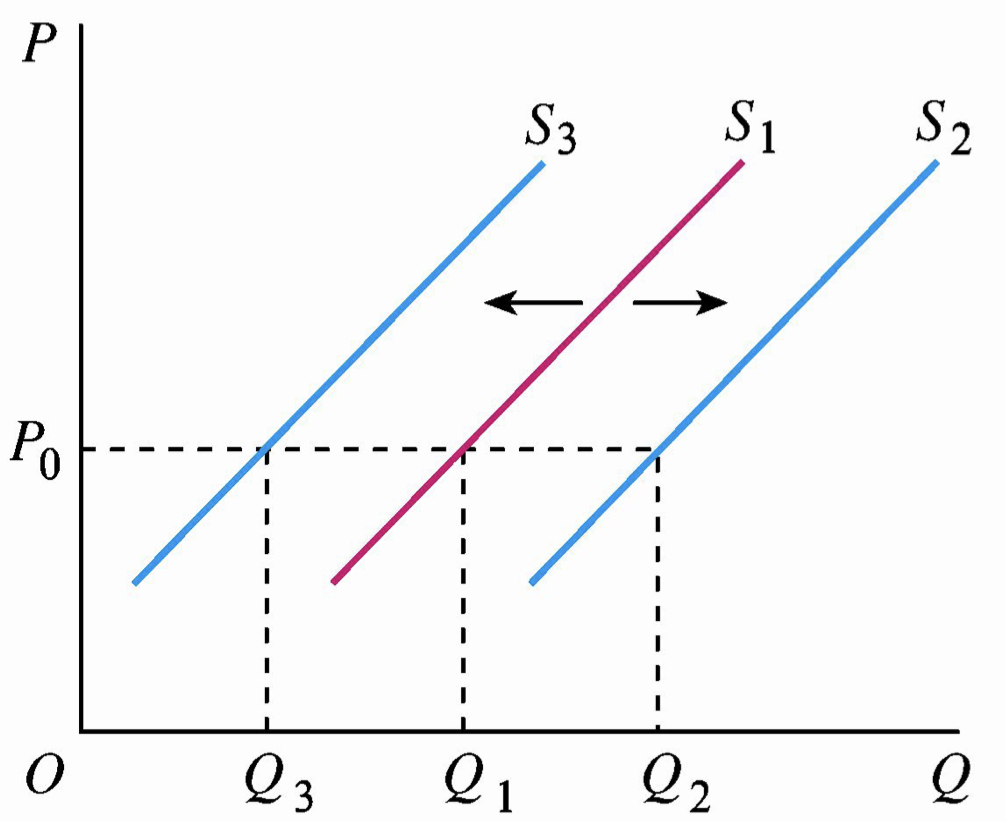
供给的变动

　　供给量的变动：该商品价格变化导致的变化，体现为点在供给曲线上的移动，即 \(Q_s=f(p_s)\)，如 \(A\) 点移动到 \(B\) 点。

供给量的变动

二、均衡价格与弹性理论

（一）均衡价格

1. 含义

　　均衡价格为需求量与供给量相等时的价格水平。假设需求量为 \(Q_d=-\alpha+\beta P\)，供给量为 \(Q_s=-\delta+\gamma P\)，那么由 \(Q_d=Q_s\) 可以计算出均衡价格。

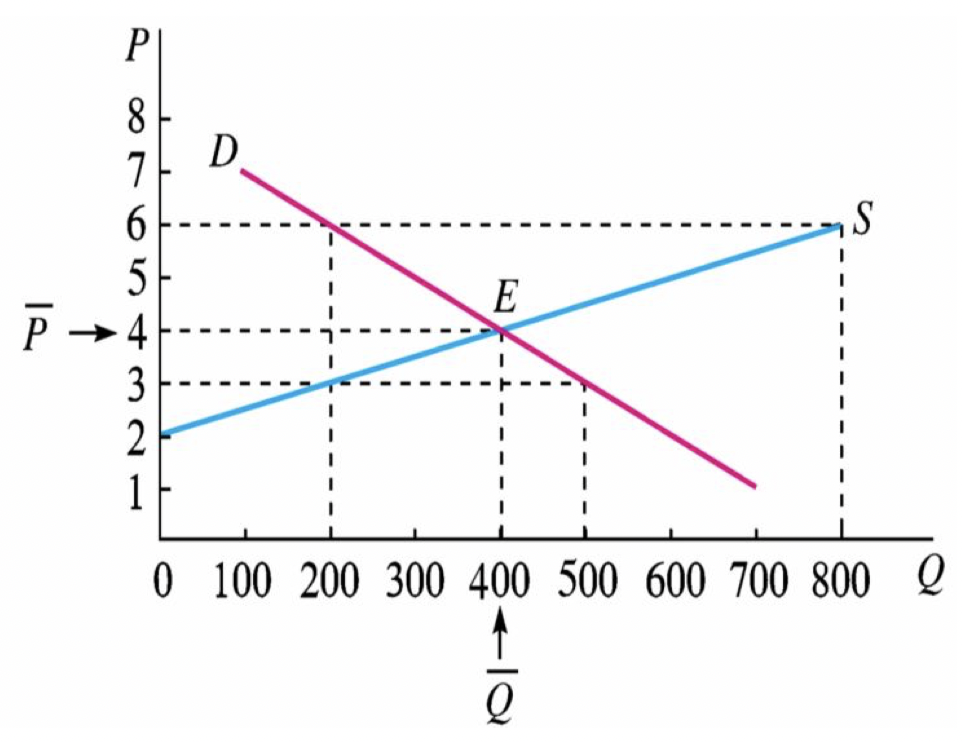
均衡价格的决定

2. 应用

2.1 支持价格/最低限价

　　定义：政府为了扶持某一行业的生产而规定的该行业产品的最低价格。支持价格一般高于市场决定的均衡价格。

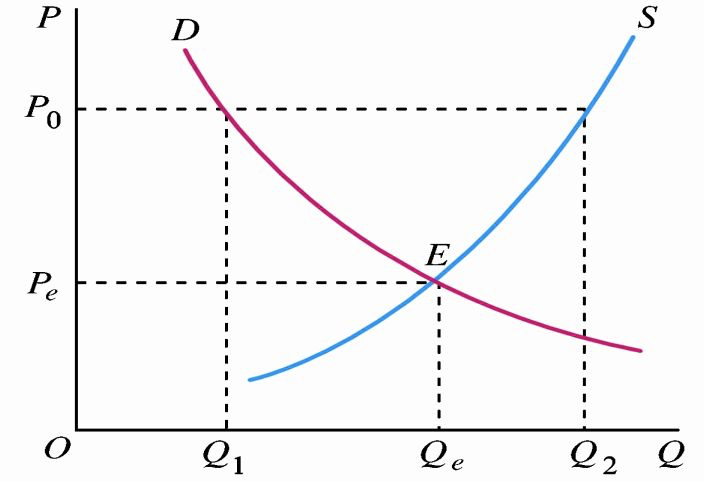
最低限价示意图

　　目的：通常是为了扶持某些行业的发展（如农业）。

　　为维持支持价格可以采取的措施：

收购过剩商品
对该商品的生产实行产量限制
对购买者给予补贴

2.2 限制价格

　　定义：政府为了限制某些商品的价格而规定的低于市场均衡价格的最高价格。（传送门："最高限价的无谓损失"）

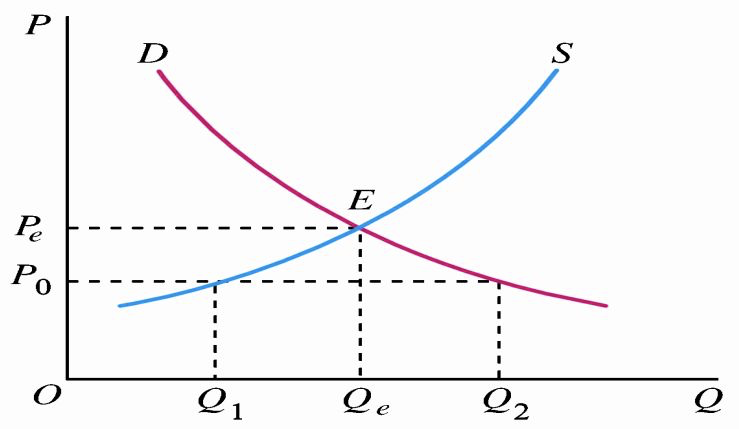
限制价格示意图

　　目的：抑制某些产品的价格上涨，尤其是为了应对通货膨胀。

　　不良影响：

供不应求会导致消费者排队抢购和黑市交易盛行；
生产者可能粗制滥造，降低产品质量。

　　为限制价格政府需要采取的措施：

通过配给制等方式控制需求量（如：生产配额）
限定消费者购买数量（如：粮票、肉票、布票）

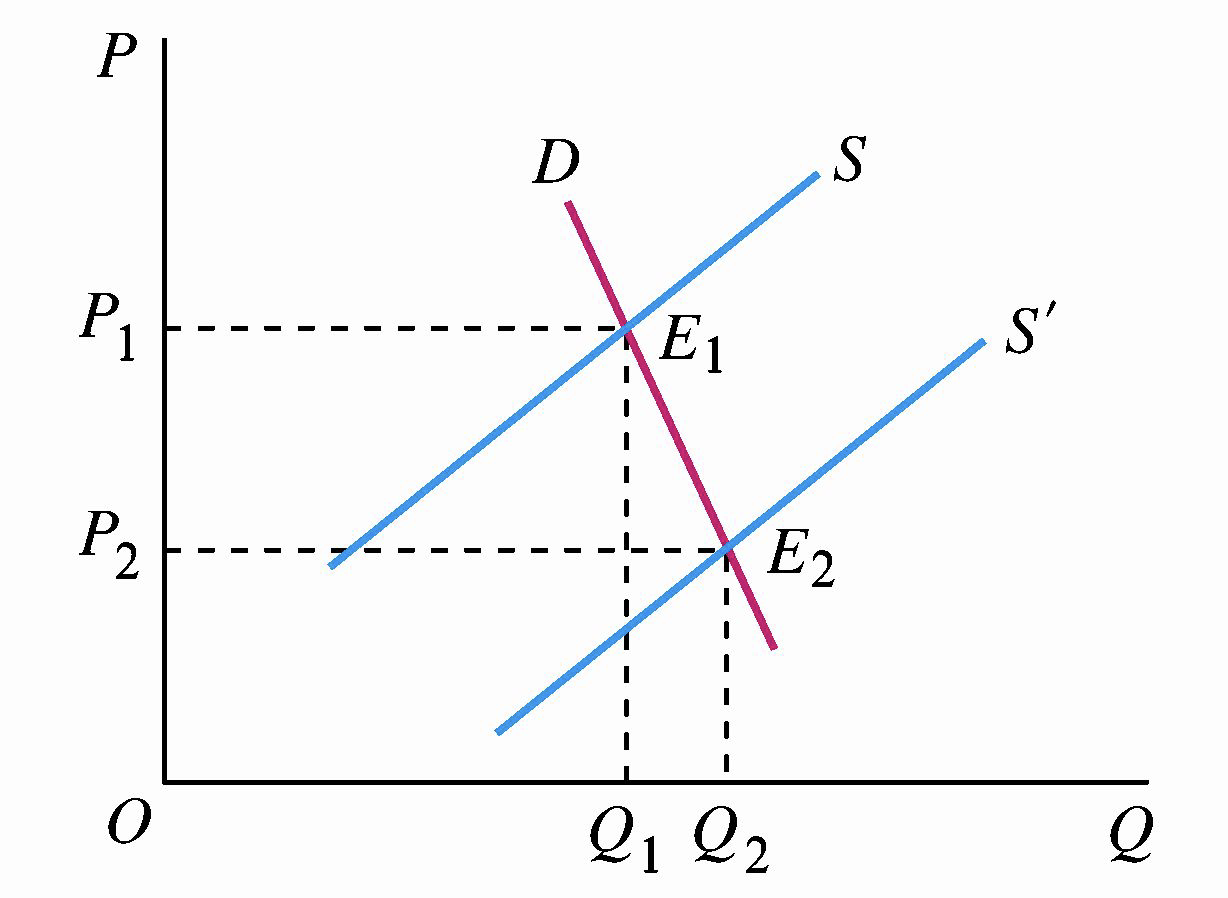
2.3 “谷贱伤农”的经济学解释

　　在农业生产活动中，存在着一种经济现象：在丰收的年份，农民的收入反而减少了，这种现象在我国民间被形象地概括为“谷贱伤农”。

　　造成“谷贱伤农”这种经济现象的根本原因在于：农产品的需求量变动带来的收入增加无法弥补价格下降导致的收入减少损失，其需求价格弹性往往小于 1 。

缺乏弹性的需求曲线与谷贱伤农

（二）弹性理论

1. 弹性的含义

　　因变量对自变量变动的反应程度/敏感程度，一般可以定义为：

\[ \begin{align} 弹性系数=\frac {因变量的变动比例} {自变量的变动比例} \end{align} \]

　　也可以写作：

\[ \begin {align} e=\frac {\Delta Y /Y} {\Delta X /X} =\frac {\Delta Y} {\Delta X} \times \frac X Y \end {align} \]

　　弧弹性的公式：\(e =\frac {\Delta Y} {\Delta X} \times \frac X Y\)

　　弧弹性的中点公式：\(e =\frac {\Delta Y} {\Delta X} \times \frac {(X_1 + X_2)/2} {(Y_1 + Y_2)/2}\)（使用中点值替代端点值）

　　点弹性的公式：\(e =\frac {d Y} {d X} \times \frac X Y\)

2. 需求价格弹性

2.1 计算方法

　　需求量与价格之间往往呈反比关系，因此在需求价格弹性取了负号。

　　需求价格弧弹性：\(e_d =- \frac {\Delta Q_d} {\Delta P} \times \frac {(P_1 + P_2)/2} {(Q_{d1} + Q_{d2})/2}\)

　　需求价格点弹性：\(e_d =- \frac {d Q_d} {d P} \times \frac P {Q_d}\)

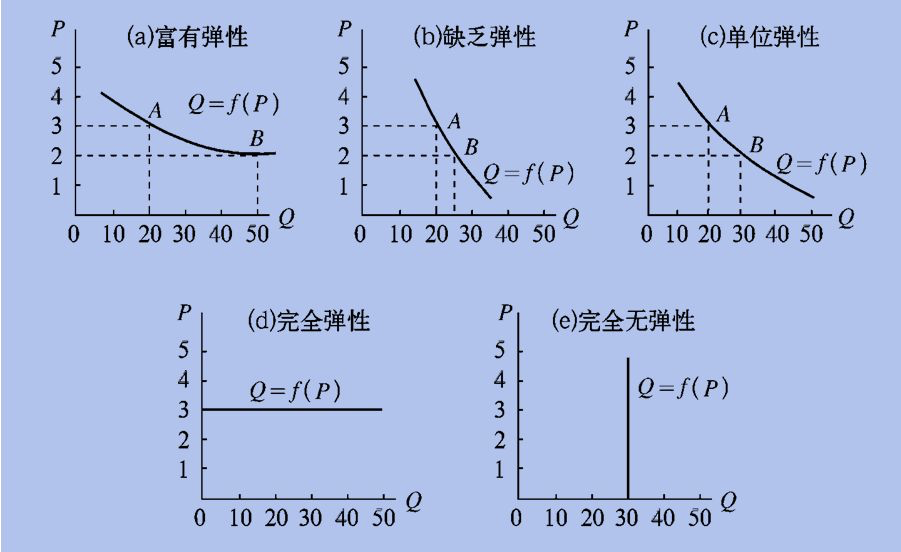
2.2 需求价格弧弹性的分类

　　根据弧弹性的大小，可以将商品的需求量与价格的关系分为以下 5 类：

富有弹性：\(|e_d|>1\)，需求量变化的幅度比价格变化的幅度更大，需求弹性比较平缓
单位弹性：\(|e_d|=1\)，需求曲线为双曲线 \(Q=\frac a P\) 的情况下，弧弹性处处相等且均为 1
缺乏弹性：\(0<|e_d|<1\)，需求量变化的幅度比价格变化的幅度更小，需求曲线比较陡峭
完全弹性：\(|e_d| = \infty\)，在给定价格下，需求量源源不断
完全无弹性：\(|e_d| = 0\)，价格变动对需求量没有影响

需求价格弧弹性的 5 种类型

2.3 线性需求曲线的需求价格弹性

　　假设线性需求函数为：\(Q_d=a-bP\)，那么需求曲线的斜率为 \(-\frac 1 b\)。

　　我们关注需求价格弹性的绝对数值，因此不再考虑负号（区别于"需求收入弹性"），上述线性需求函数的需求价格点弹性为：

\[ \begin {align} e_d= b \times \frac P Q= \frac {bP } {a-bP} \end {align} \]

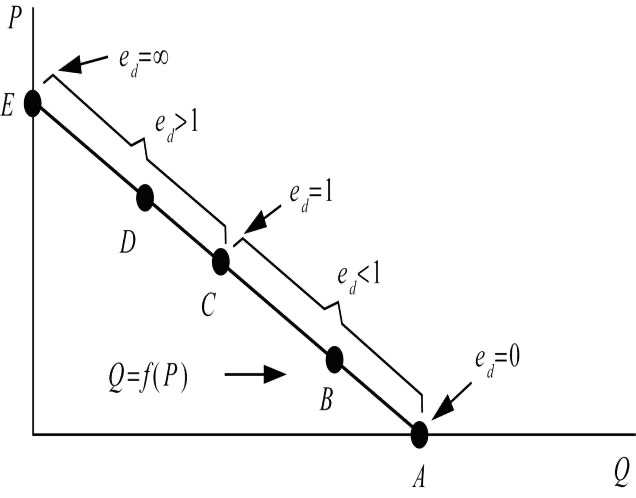
线性需求函数点弹性的 5 种类型

　　当 \(e_d=1\) 时，\(bP=a-bP\)，可以算出此时 \(P=\frac a {2b},Q=\frac a 2\)，即需求函数的 \(C\) 点为单位弹性，也就是说：

在中点 \(C\) 点（线段中点）处，需求价格弹性为 \(e_d=1\)；
在中点 \(C\) 点的下方，\(A\) 点与 \(B\) 点的需求价格弹性 \(e_d<1\)；
在中点 \(C\) 点的上方，\(D\) 点与 \(E\) 点的需求价格弹性 \(e_d>1\)。

理解补充：

在线性需求函数中，可以从以下方面理解点的位置与点弹性大小的关系：

线性需求函数上，价格和需求量呈线性变化关系。

线段 \(AC\)：价格 \(P\) 较小，需求量 \(Q\) 较大，此时价格下降 1 单位，价格变动的比例相对较大，需求量变动比例相对较小（即弹性公式 \(e=\frac {\Delta Q / Q} {\Delta P /P}\) 的分母更大），因此弹性小于 1；

线段 \(CE\)：价格 \(P\) 较大，需求量 \(Q\) 较小，此时价格下降 1 单位，价格变动的比例相对较小，需求量变动比例相对较大（即弹性公式 \(e=\frac {\Delta Q / Q} {\Delta P /P}\) 的分子更大），因此弹性大于 1。

2.4 需求价格弹性的影响因素

商品的可替代性
商品用途的广泛性
商品对消费者生活的重要程度
商品的消费支出在消费者预算总支出中所占的比重
所考察的消费者调节需求量的时间

3. 需求收入弹性

3.1 计算方法

　　需求量与收入之间一般呈正相关系，因此不取负号（区别于"需求价格弹性"）。

　　需求收入弹性的计算方式：\(e_M=\frac {\Delta Q} {\Delta M} \times \frac M Q\)，或者写成点弹性：\(e_M =\frac {d Q} {d M} \times \frac M Q\)

3.2 商品分类

正常品：\(e_M>0\)，随着收入的增加，消费者对正常商品的需求量会上升
- 奢侈品/高档品：\(e_M>1\)，属于富有弹性（需求收入弹性）的商品
- 必需品：\(0<e_M<1\)，属于缺乏弹性（需求收入弹性）的商品，如食品消费
劣等品：\(e_M<0\)，随着收入的增加，消费者对劣等商品的需求量会下降

　　恩格尔定律：在一个家庭或一个国家中，食品支出在收入中所占的比例随着收入的上升而下降，即国家或家庭越富裕，食品支出的收入弹性就越小。

4. 需求交叉弹性

4.1 定义与计算方法

　　定义：在一定时期内，一种商品的需求量变动对于它的相关商品的价格变动的反应程度。

　　商品 X 的需求量与商品 Y 的价格相关，设 \(Q_X=f(P_Y)\)，那么：

　　需求交叉价格的弧弹性公式：\(e_{XY}=\frac {\Delta Q_X} {\Delta P_Y} \times \frac {P_Y} {Q_X}\)

　　需求交叉价格的点弹性公式：\(e_{XY}=\frac {d Q_X} {d P_Y} \times \frac {P_Y} {Q_X}\)

4.2 需求交叉弹性与商品分类

　　根据需求交叉弹性，两种商品的关系可以分为以下三种类型：

替代品：\(e_{XY}>0\)，表示提高商品 Y 的价格能提高商品 X 的需求量，\(|e_{XY}|\) 越大，替代性越强；
互补品：\(e_{XY}<0\)，表示提高商品 Y 的价格会降低商品 X 的需求量，\(|e_{XY}|\) 越大，互补性越强；
不相关商品：\(e_{XY}=0\)，表示商品 X、商品 Y 是相对独立的两种商品。

5. 供给价格弹性

5.1 计算方法

　　供给量与价格之间往往呈正比关系。

　　供给价格弧弹性：\(e_s =\frac {\Delta Q_s} {\Delta P} \times \frac P {Q_s}\)

　　供给价格点弹性：\(e_s = \frac {d Q_s} {d P} \times \frac P {Q_s}\)

5.2 供给价格弹性的分类

　　根据供给价格弹性的大小，可以将商品的供给量与价格的关系分为以下 5 类：

富有弹性：\(e_s>1\)，供给量变化的幅度比价格变化的幅度更大
缺乏弹性：\(0<e_s<1\)，供给量变化的幅度比价格变化的幅度更小
单位弹性：\(e_s=1\)，供给量变化幅度与价格变动程度相等，是一种极端情况
完全弹性：\(e_s = \infty\)，供给曲线为一条水平线，这是商品出现严重过剩时的情况
完全无弹性：\(e_s = 0\)，供给曲线为一条垂直线，价格变动对供给量没有影响，一般是极其稀缺、珍贵或无法复制的商品。

5.3 供给价格弹性的影响因素

生产的难易程度
生产规模与规模变化的难易程度
成本的变化
时间的差异、厂商的生产能力、对未来价格的预期

6. 蛛网模型

6.1 简介

　　蛛网模型运用弹性原理解释某些生产周期较长的商品在失去均衡时发生的不同波动情况的一种动态分析理论。

　　基本假设：

供给有时滞：商品的本期产量取决于前一期的价格，即供给函数为：\(Q_t^s=f(P_{t-1})\)
需求无时滞：商品本期的需求量取决于本期的价格，即供给函数为：\(Q_t^d=f(P_{t})\)

　　使用方程表示：

供给有时滞：\(Q_t^s=-\delta+\gamma P_{t-1}\)
需求无时滞：\(Q_t^d=\alpha-\beta P_t\)
本期供需均衡：\(Q_t^s=Q_t^d\)

　　因此，可以求得 \(P_t\) 与 \(P_{t-1}\) 的关系：

\[ \begin{align} P_t = - \frac \gamma \beta P_{t-1} + \frac { \alpha + \delta } {\beta} \end{align} \]

　　令期初价格为 \(P_0\)，那么：

\[ \begin {equation} \begin {split} P_t & = \left( - \frac {\gamma} {\beta } \right) ^ t \cdot P_0 + \left\{ \frac { \alpha + \delta } {\beta} \left[ 1+ \left(- \frac {\gamma} {\beta } \right)^1 + \left(- \frac {\gamma} {\beta } \right)^2+ ...+\left(- \frac {\gamma} {\beta } \right)^{t-1} \right] \right\} \\\\ & = \left( - \frac {\gamma} {\beta } \right) ^ t \cdot P_0 + f \end {split} \end {equation} \]

　　我们将上式花括号设为 \(f\) 单独计算。其中，方括号内为一个首项为 \(a_0=1\)、公比为 \(q=- \frac {\gamma} {\beta}\) 的等比数列，可以使用等比数列的求和公式求解。

数学补充：等比数列求和公式

假设一个等比数列 \(A_n\) 的公比为 \(\frac {a_n} { a_{n-1} }=q\)，如果 \(a_n \neq 0\) 且 \(q \neq 1\)，则其前 \(n\) 项之和为：

\[ S_n=a_1 \cdot \frac {1-q^n} {1-q} \]

　　因此上式第一行花括号内的式子可以写作：

\[ \begin{align} \begin {split} f & = \frac { \alpha + \delta } {\beta} \left[ 1+ \left(- \frac {\gamma} {\beta } \right)^1 + \left(- \frac {\gamma} {\beta } \right)^2+ ...+\left(- \frac {\gamma} {\beta } \right)^{t-1} \right] \\ & = \frac { \alpha + \delta } {\beta} \left [ 1 \cdot \frac {1- (-\frac {\gamma} {\beta} )^t} {1- (-\frac {\gamma} {\beta} )} \right] \\ & = \frac { \alpha + \delta } {\beta} \cdot \frac {1- (-\frac {\gamma} {\beta} )^t} {(\gamma + \beta) / {\beta} } \\ & = \frac { \alpha + \delta } {\gamma + \beta} \left[ 1- \left(-\frac {\gamma} {\beta} \right)^t \right] \end{split} \end{align} \]

　　计算过程中上式的第四行分母消去了 \(\beta\)。因此，"原式"的 \(P_t\) 即可表示为：

\[ \begin {align} P_t & = \left( - \frac {\gamma} {\beta } \right) ^ t \cdot P_0 + f \notag \\ & = \left( - \frac {\gamma} {\beta } \right) ^ t \cdot P_0 + \frac { \alpha + \delta } {\gamma + \beta} \left[ 1- (-\frac {\gamma} {\beta} )^t \right] \notag \\ & = \left( P_0 - \frac { \alpha + \delta } {\gamma + \beta} \right ) \cdot \left ( - \frac {\gamma} {\beta } \right) ^ t + \frac { \alpha + \delta } {\gamma + \beta} \notag \\ \end {align} \]

　　考虑到均衡价格为 \(P_e = P_t = P_{t-1}\)，因此 \(P_e=\frac {\alpha + \delta} {\beta + \gamma}\)，代入上式可得：

\[ \begin {align} P_t=(P_0- P_e) \left (- \frac \gamma \beta \right)^t + P_e \end {align} \]

　　因此，蛛网模型主要包括三种情况。

6.2 蛛网模型的 3 种情况

　　对于某一种商品，供给价格弹性与需求价格弹性的相对大小关系不同，商品的价格均衡情况会有所不同。

6.2.1 收敛型蛛网：供给弹性小于需求弹性

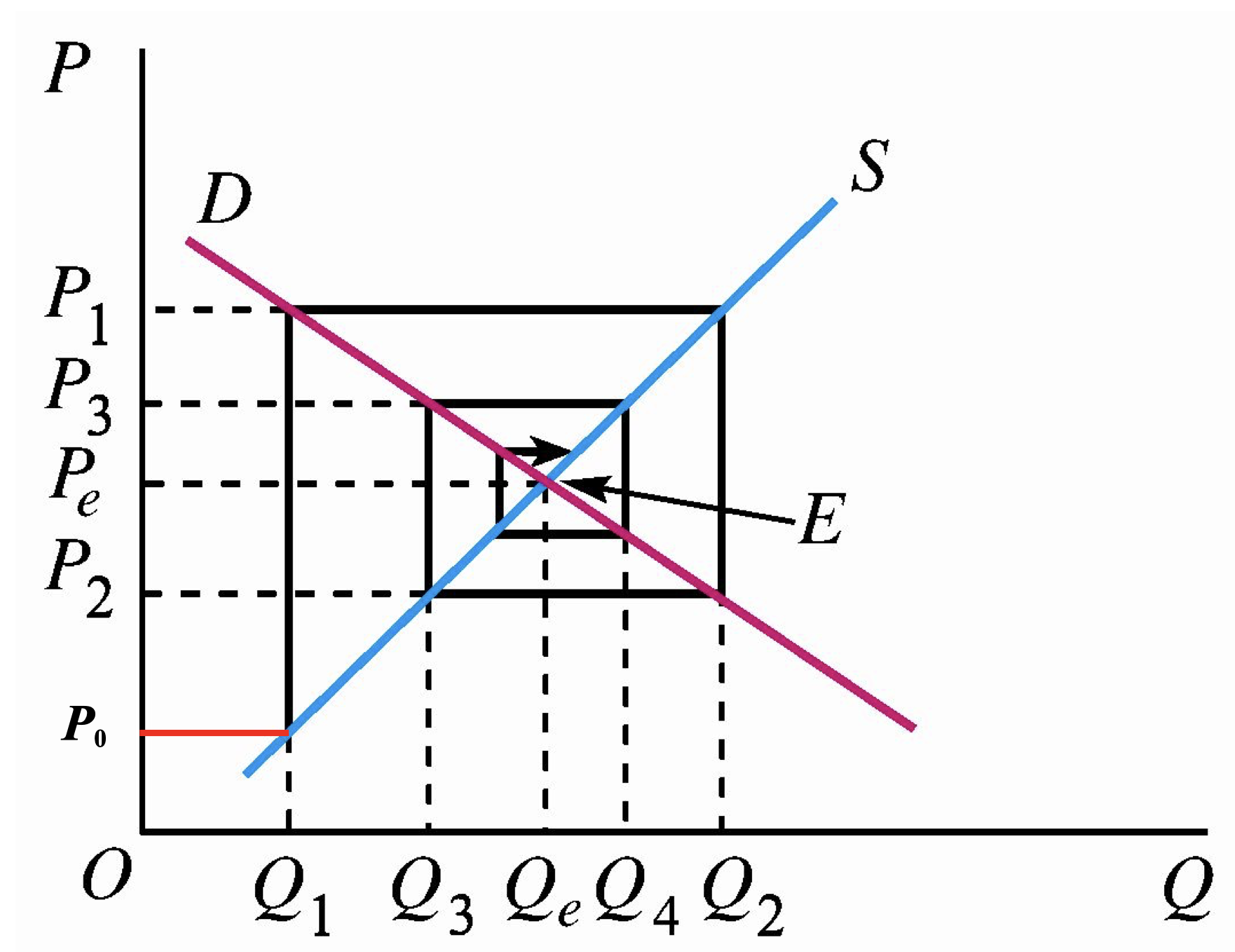
　　当 \(t \to \infty\)，如果 \(\frac \gamma \beta<1\)，那么 \(P_t \to P_e\)，也就是说随着时间 \(t\) 的增加，若 \(\gamma < \beta\)，供给曲线比需求曲线更陡峭（斜率更大），供给弹性小于需求弹性。此时，供给变动对价格变动的反应程度小于需求变动对价格变动的反应程度，此时，价格最后自发地趋向于均衡水平。

收敛型蛛网

理解补充：

需求价格弹性：\(e_d =- \frac {d Q_d} {d P} \times \frac P {Q_d}\)

供给价格弹性：\(e_s = \frac {d Q_s} {d P} \times \frac P {Q_s}\)

斜率公式：\(k=\frac {dP} {dQ}\)，需求曲线斜率为\(k_d=\frac {dP} {dQ_d}\)，供给曲线斜率为\(k_s=\frac {dP} {dQ_s}\)

需求价格弹性与供给价格弹性都与曲线斜率绝对值呈负相关，因此\(e_s < e_d\)意味着供给函数曲线更加陡峭；

画图方向：逆时针旋转，箭头方向为时间变化方向表明供给有时滞，需求无时滞。

在\(t=1\)时期，企业供给按照价格\(P_0\)供给商品\(Q_1\)，市场实际价格为\(P_1\)；

在\(t=2\)时期，企业按照上一期价格\(P_1\)供给商品\(Q_2\)，市场实际价格为\(P_2\)；

...

企业生产决策的价格与市场实际价格的差异越来越小，最终向市场均衡价格\(P_e\)收敛。

6.2.2 发散型蛛网：供给弹性大于需求弹性

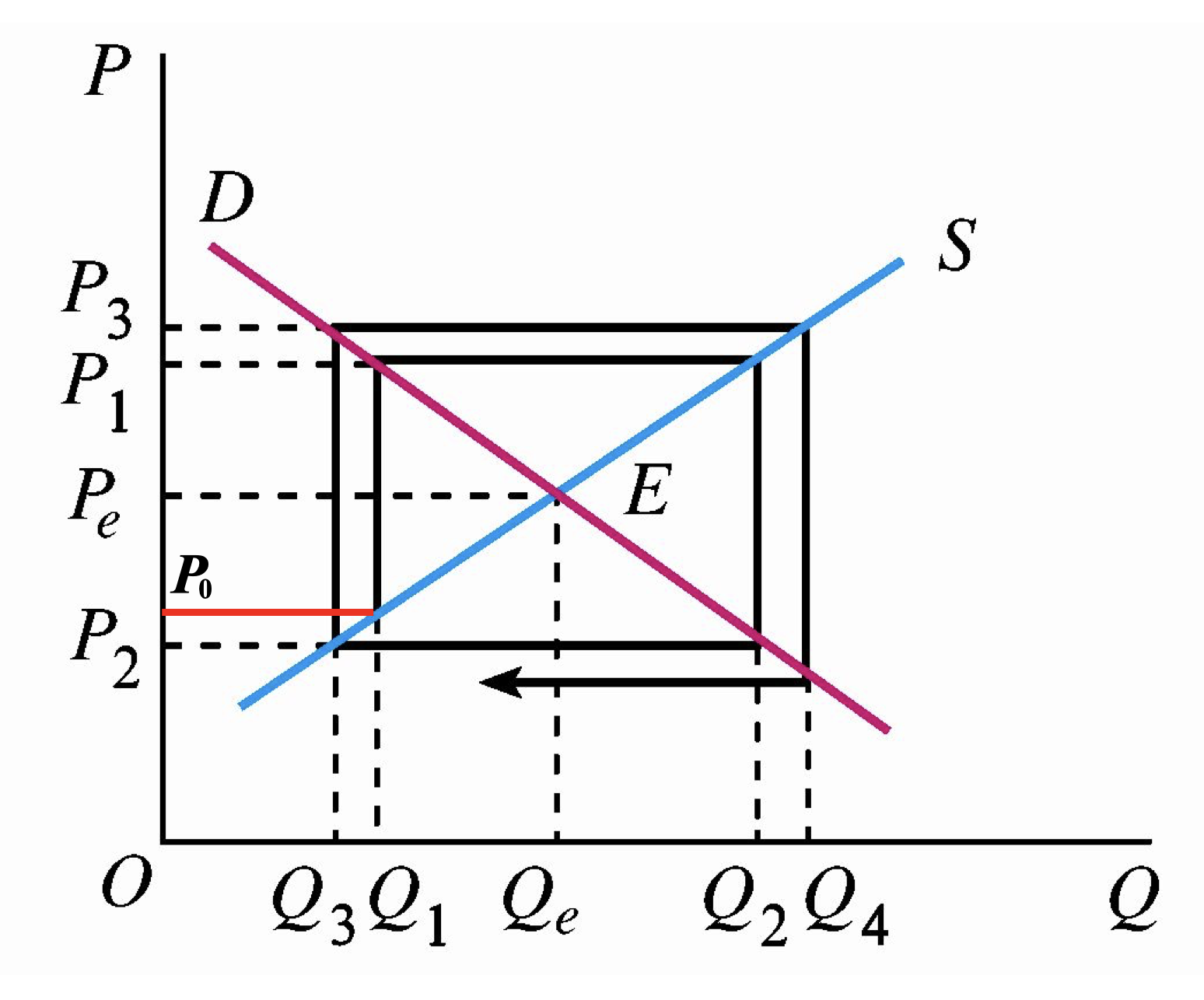
　　当 \(t \to \infty\)，如果 \(\frac \gamma \beta>1\)，那么 \(P_t \to \infty\)，也就是说随着时间 \(t\) 的增加，若 \(\gamma > \beta\)，供给曲线比需求曲线更平坦（斜率更小），供给弹性大于需求弹性。此时，供给变动对价格变动的反应程度要大于需求变动对价格变动的反应程度，此时，价格波动对产量的影响越来越强，最后离均衡越来越远。

发散型蛛网

理解补充：

\(e_s > e_d\)，意味着供给函数曲线更加平坦，需求曲线更加陡峭；

画图方向：逆时针旋转，箭头方向为时间变化方向表明供给有时滞，需求无时滞。

在\(t=1\)时期，企业供给按照价格\(P_0\)供给商品\(Q_1\)，市场实际价格为\(P_1\)；

在\(t=2\)时期，企业按照上一期价格\(P_1\)供给商品\(Q_2\)，市场实际价格为\(P_2\)；

...

企业生产决策的价格与市场实际价格的差异越来越大，最终会偏离市场均衡价格\(P_e\)越来越远。

6.2.3 封闭型蛛网：供给弹性等于需求弹性

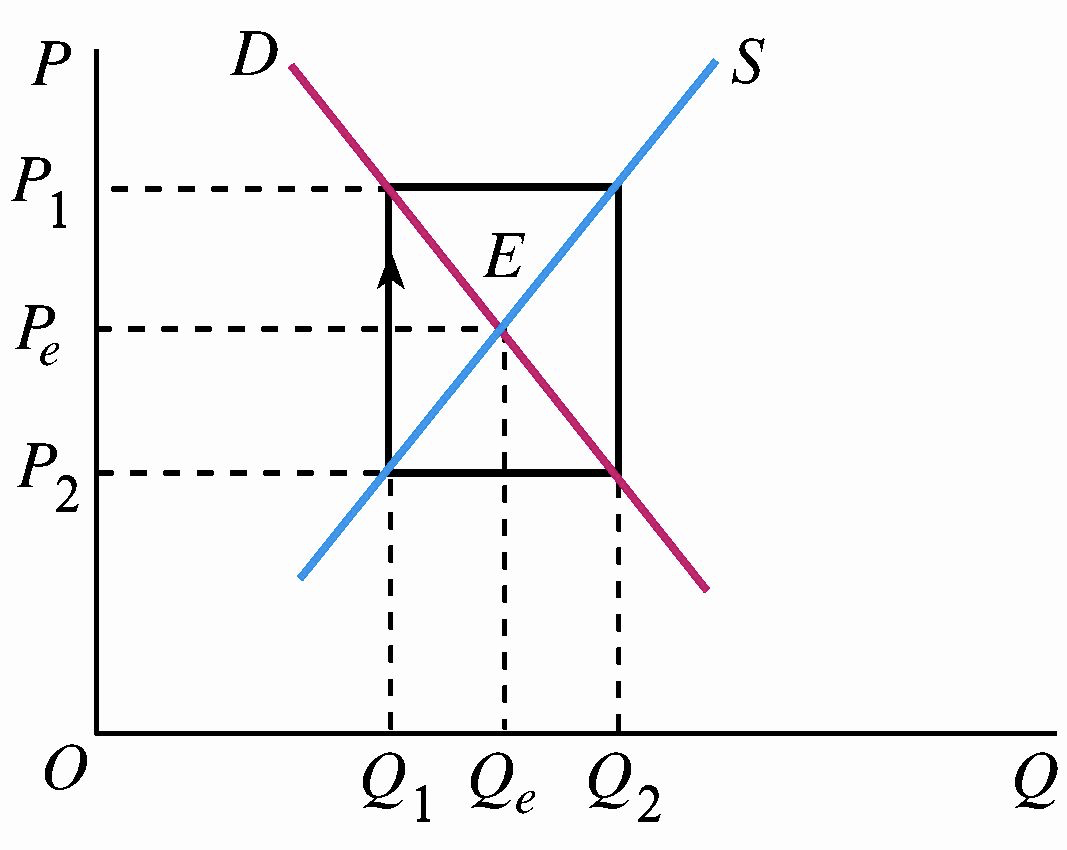
　　当 \(t \to \infty\)，如果 \(\frac \gamma \beta =1\)，那么 \(P_t\) 为一个常数，也就是说随着时间 \(t\) 的增加，若 \(\gamma = \beta\)，供给曲线与需求曲线斜率相等，供给弹性等于需求弹性。此时，供给变动对价格变动的反应程度与需求变动对价格变动的反应程度相等，即价格与产量的波动始终保持相同的程度。

封闭型蛛网

理解补充：

\(e_s = e_d\)，意味着供给函数与需求函数的曲线一样平坦；

画图方向：逆时针旋转，箭头方向为时间变化方向表明供给有时滞，需求无时滞。

在\(t=1\)时期，企业供给按照价格\(P_0=P_2\)供给商品\(Q_1\)，市场实际价格为\(P_1\)；

在\(t=2\)时期，企业按照上一期价格\(P_1\)供给商品\(Q_2\)，市场实际价格为\(P_2\)；

...

企业生产决策的价格只会在\(P_2\)、\(P_1\)之间变化，市场无法自发达到均衡，也不会偏离均衡。

相关资源：