微观|第8章:要素市场理论—生产要素的价格决定
【内容速查与目录】
【笔记下载】
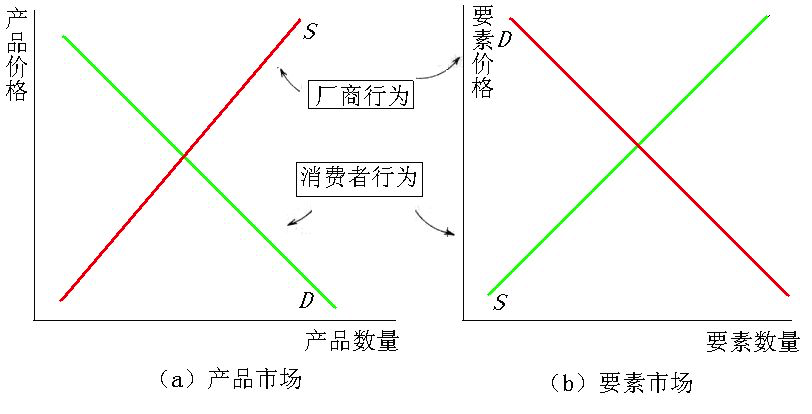
一、产品市场与要素市场
补充:
- 消费者:产品市场-商品需求主体,要素市场-要素供给主体
- 厂商:产品市场-商品供给主体,要素市场-要素需求主体
二、生产要素的需求
(一)引致需求与联合需求
1. 引致需求
对生产要素的需求产生于对利润最大化的需求;
对生产要素的需求受到消费者对产品需求的影响。
具体来看:
- 第一,在生产要素市场上,需求不是来自消费者,而是来自厂商。从这个意义上来说,对生产要素的需求不是直接需求,而是“间接”需求。
- 第二,厂商通过购买生产要素进行生产并从中获得收益,部分地要取决于消费者对其所生产的产品的需求。从这个意义上说,生产要素的需求又是所谓“派生”需求或“引致”需求。
- 第三,对生产要素的需求还有个特点,就是所谓“共同性”,即对生产要素的需求是共同的、相互依赖的需求。
2. 联合需求
对生产要素的需求是共同的、相互依赖的;
对生产要素的需求往往取决于多种生产要素的价格。
(二)生产要素价格决定的需求方面
1. 厂商要素需求一般原则
1.1 主要假定
假定:每个厂商使用一种生产要素,生产单一产品,追求最大限度的利润。
1.2 边际收益产品 (边际要素收益)
设厂商只使用一种可变要素 \(X\)。 若增加的要素量为 \(\Delta X\),由此带来的收益增量为 \(\Delta R\),得要素的边际收益产品 \(MRP\) (marginal revenue product) 为:
\[ \begin {align} \frac {dR} {dX}=\lim_{\Delta X \to 0} \frac {\Delta R } {\Delta X} \end {align} \]
要素的边际收益产品等于要素的边际产品和产品的边际收益的乘积,即:
\[ \begin {align} \frac {dR} {dX}=\frac {dR} {dQ} \cdot \frac {dQ} {dX} \end {align} \]
或者表示为:
\[ \begin {align} MRP=MR \cdot MP \end {align} \]
1.3 边际要素成本
用 \(\Delta X\) 表示要素增量,由此引起的成本增量用 \(\Delta C\) 表示,那么边际要素成本 \(MFC\) 为:
\[ \begin {align} \frac {dC} {dX}=\lim_{\Delta X \to 0} \frac {\Delta C } {\Delta X} \end {align} \]
类似于产品市场,要素价格是要素供给量的函数,用 \(W\) 表示要素价格,那么要素供给函数为 \(W(X)\),则成本函数为 \(W(X) \cdot X\),于是边际要素成本为:
\[ MFC=\frac {d \big[W(X) \cdot X \big]} {dX}=W(X)+X \cdot \frac {d \big[W(X) \big]} {dX} \]
边际要素成本还可以写成:
\[ \begin {align} MFC=MC \cdot MP \end {align} \]
数学补充:
\[ \begin{align} MFC & =\frac {d \big[W X \big]} {dX} = \frac {d \big[W X \big]} {dQ} \cdot \frac {d Q} {dX} \notag \\ & = MC \cdot MP \end{align} \]
其中:\(\frac {d Q} {dX}\) 为要素的边际产出 \(MP\);\(\frac {d \big[W X \big]} {dQ}\) 为成本函数对产量的导数,即为边际成本 \(MC\)。
经济含义:边际要素成本表示在其他要素投入不变的前提下,某一要素的投入量发生变化带来的成本增量。考虑到要素投入是用于生产,这部分成本可以分解为要素的边际产出 \(MP\) 与生产商品的边际成本 \(MC\) 两个部分,即增加某一要素投入导致的边际产出发生变动,这部分产出变动对应的边际成本(相乘)就是增加要素投入的边际成本 \(MFC\)。
1.4 一种可变要素情况下要素需求原则
厂商使用要素的原则是要素的边际收益产品等于边际要素成本,即:\(MRP=MFC\),即要素投入的边际成本等于其带来的边际收益。
利润函数为:\(\pi (X)=R \big[Q(X) \big]-C \big[Q(X) \big]\)
利润最大化条件为:
\[ \begin {align} \frac {d \pi (X)} {d X} = \frac {dR} {dQ} \cdot \frac {dQ} {dX} - \frac {dC} {dQ} \cdot \frac {dQ} {dX} =0 \end {align} \]
即:\(MR \cdot MP=MC \cdot MP \ \ \ \Longrightarrow \ \ \ MR=MC\)
由此可见,厂商使用要素的原则与利润最大化产量的条件实质上是一回事。
1.5 延伸:关于 MRP 与 VMP
1.5.1 概念:
边际收益产品 \(MRP\):增加一单位要素使用所增加的总收益。
\[ \begin {align} MRP_L=\frac {\Delta TR } {\Delta L } = MR \times MP_L \end {align} \]
边际产品价值 \(VMP\):增加一单位要素使用所增加的产品的市场价值。
\[ \begin {align} VMP_L=\frac {\Delta V} {\Delta L } = P \times MP_L \end {align} \]
1.5.2 产品价格变动的影响
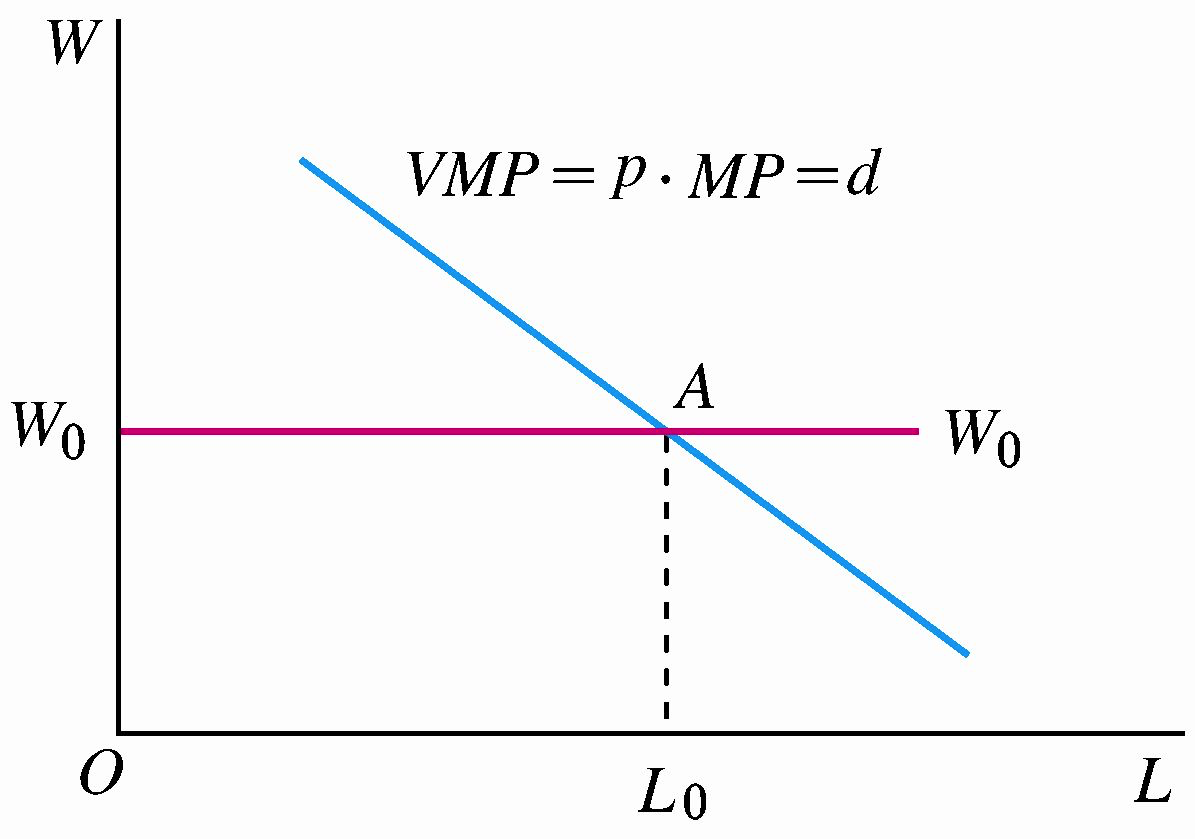
(1)若产品价格是不变的(产品市场完全竞争),则:\(MRP=VMP\)
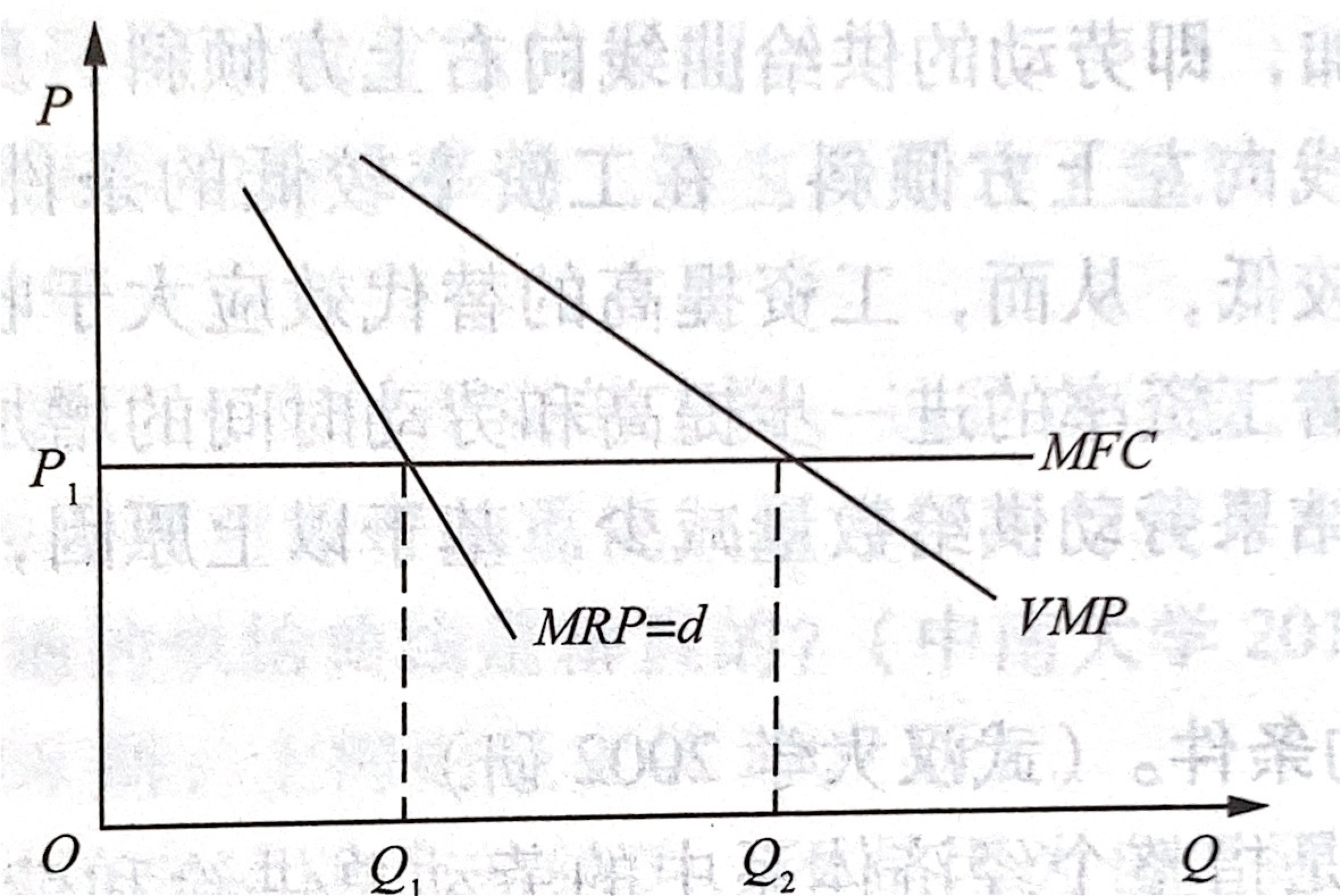
(2)若产品价格随着销量的增加而下降(产品市场不完全竞争),则:\(MRP<VMP\)
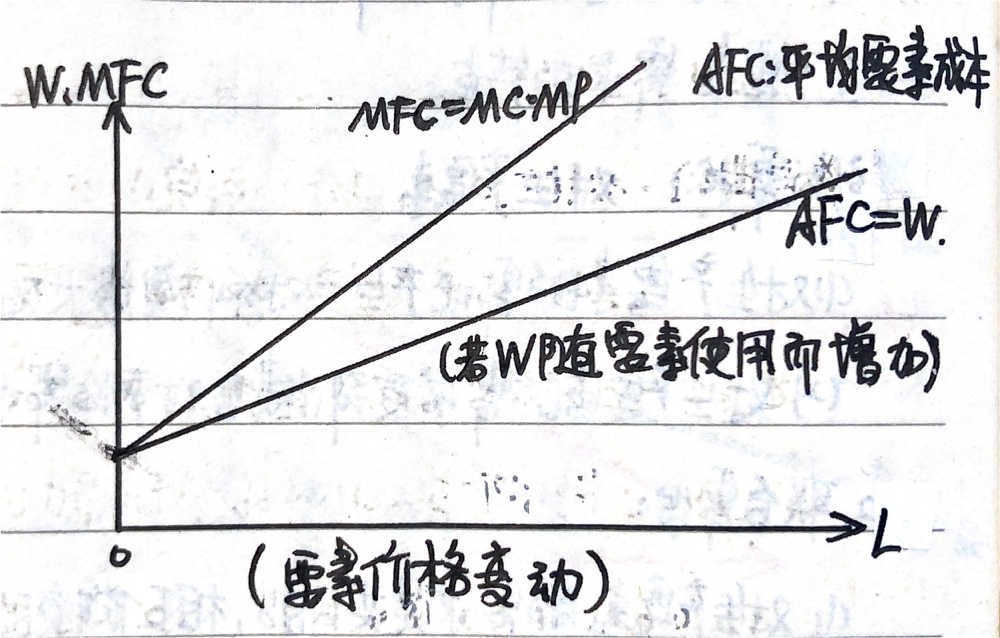
1.5.3 要素价格变动(以劳动市场为例)
(1)要素价格是不变的(要素市场完全竞争),则:\(MFC=W\)

(2)要素价格随使用量增加而增加(要素市场不完全竞争),则:\(MFC>W\)
2. 厂商要素需求原则的简化
厂商使用生产要素,遵循增加单位要素使用所增加的总收益等于所增加的成本,即:
\[ \begin {align} MRP=MFC \end {align} \]
三种情况:
- 对于完全竞争厂商,要素需求原则为:\(P \cdot MP=W\)
- 对于卖方垄断厂商,要素需求原则为:\(MR \cdot MP=W\)
- 对于买方垄断厂商,要素需求原则为:\(P \cdot MP = MC \cdot MP\)
3. 完全竞争、卖方垄断、买方垄断厂商要素需求原则比较
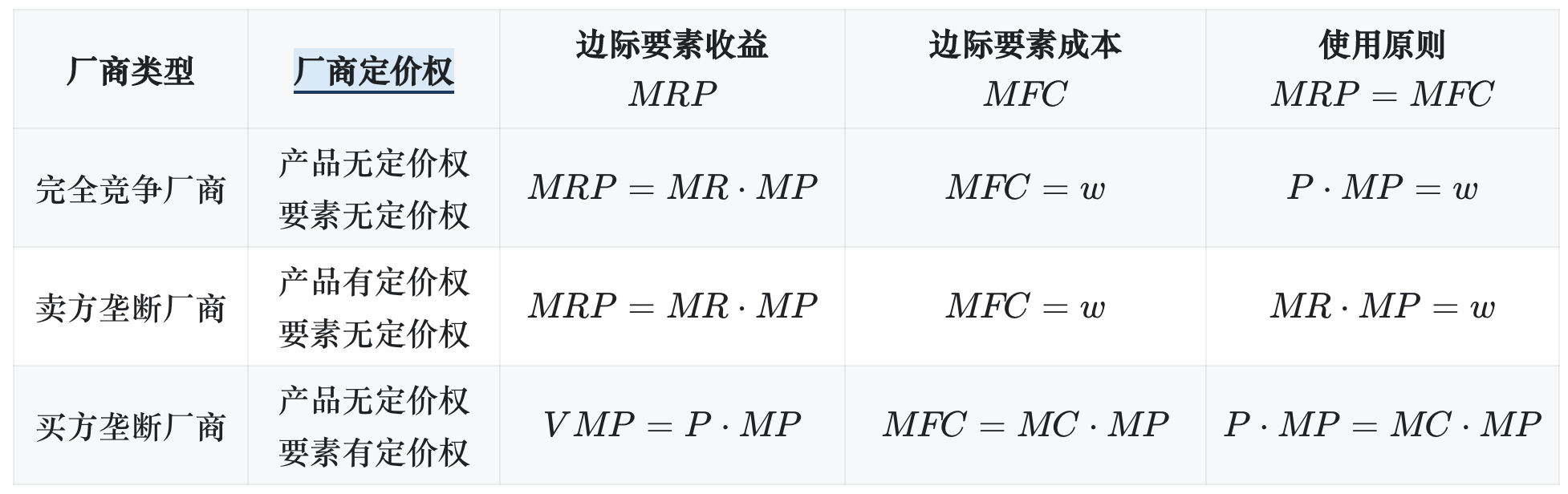
补充:
- "完全竞争厂商":\(VMP=MRP\)、\(MFC=W\)
- "卖方垄断厂商":\(VMP>MRP\)、\(MFC=W\)(要素供给垄断)
- "买方垄断厂商":\(VMP=MRP\)、\(MFC>W\)(要素需求垄断)
- "买卖垄断厂商":\(VMP>MRP\)、\(MFC>W\)(要素供需垄断)
==上面表格的第二列存在疑问==
(三)完全竞争厂商的要素需求
产品市场与要素市场都是完全竞争的,此时:\(MRP=VMP\),\(MFC=W\)
1. 完全竞争要素市场的构成条件
- 要素的供求双方的数量很多(都是价格接受者);
- 生产要素之间没有区别(可替代性);
- 要素可以自由流动。
\(\Longrightarrow \ \ \ MFC=AFC=W\)
2. 竞争性厂商要素需求原则的数学推导
完全竞争厂商利润函数为:\(\pi (L)=P \cdot Q(L) - W \cdot L\)
利润最大化一阶条件为:\(\frac {d \pi (L)} {d L} = P \cdot \frac {dQ(L)} {dL} - W=0\)
即:\(P \cdot MP_L - W=0 \ \ \ \Longrightarrow \ \ \ VMP=W\)
3. 完全竞争厂商对生产要素的需求曲线
完全竞争厂商对生产要素 \(L\) 的需求函数反映的是:在其他条件不变时,完全竞争厂商对要素 \(L\) 的需求量与要素价格 \(W\) 之间的关系。要素需求函数可表示为:
\[ \begin {align} P \cdot MP_L = W \end {align} \]
上式确定了从要素价格 \(W\) 到要素使用量 \(L\) 的一个函数关系,即确定了完全竞争厂商对要素的一个需求函数。
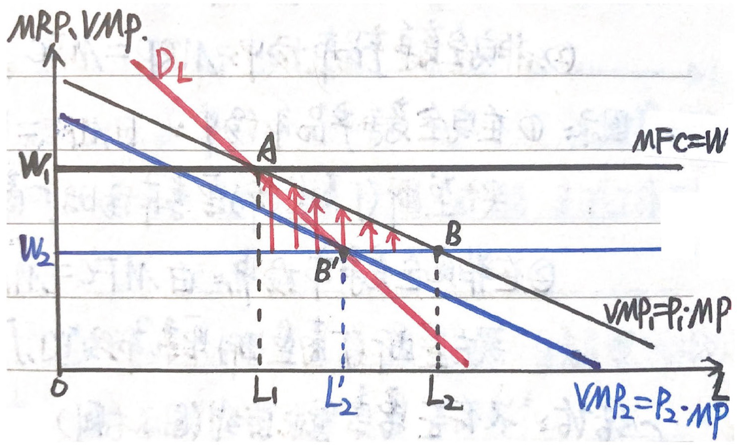
如图所示,在完全竞争的产品市场与要素市场中,由 \(VMP=W\) 可以确定在工资水平 \(W_1\) 下的劳动供需均衡点为 \(A\) 点,当劳动价格(工资水平)由 \(W_1\) 下降至 \(W_2\) 时,厂商若仍然雇佣 \(L_1\) 数量的劳动,边际产品价值 \(VMP>W_2\),其差额 \(VMP-W_2\)(图示红色箭头)为厂商使用的生产要素净利益,追求利润最大化的厂商会增加劳动雇佣数量至 \(L_2\)。
由于厂商的劳动雇佣增加,产出的产品数量也增加,对于同质化的其他完全竞争厂商也会增加劳动雇佣进而增加产出,因此市场产品总供给会上升,导致产品的市场价格由 \(P_1\) 下降至 \(P_2\),对于价格接受者的完全竞争厂商,其 \(VMP=P \times MP_L\) 也会由 \(VMP_1\) 下降至 \(VMP_2\),与 \(W_2\) 曲线相交于 \(B'\) 点,此时 \(L'_2<L_2\)。
因此:
- 若不考虑其他厂商反应:产品价格 \(P\) 保持不变,\((L_1,W_1) \ \ \to \ \ (L_2,W_2)\)
- 若考虑其他厂商反应:产品价格 \(P\) 随 \(W\) 下降,\((L_1,W_1) \ \ \to \ \ (L'_2,W_2)\)
对于完全竞争厂商,真实的劳动力需求曲线是图中的 \(D_LDL\) 曲线。\(D_LDL\)市场需求曲线即为所有厂商 \(D_L\) 曲线的加总。
根据边际生产力递减的性质,可得出以下结论:完全竞争厂商的要素需求曲线与边际产品价值曲线完全重合,向右下方倾斜。

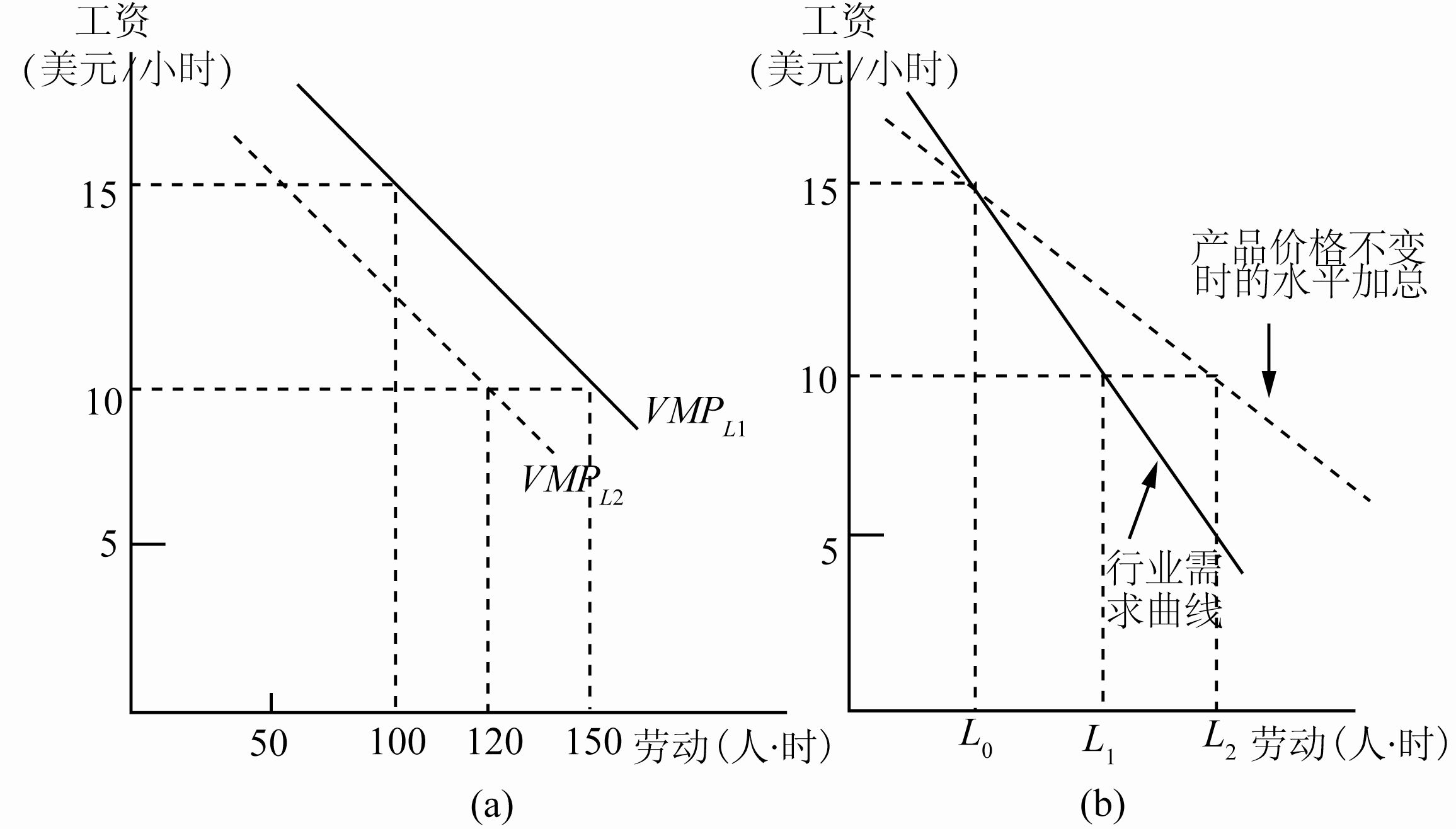
4. 市场需求曲线
为了得到总的市场需求曲线,必须首先决定每个行业对劳动的需求,然后水平地把行业的需求曲线(行业调整曲线)加总。核心在于第一步,即决定行业需求曲线,要考虑到随着投入要素价格的变动,厂商生产的产出水平及其产品价格的变动。
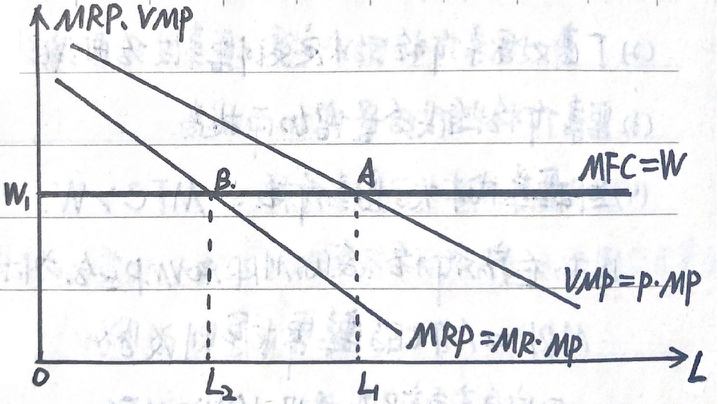
(四)卖方垄断厂商的要素需求
卖方垄断厂商面临不完全竞争的产品市场、完全竞争的要素市场,此时:\(MRP<VMP\),\(MFC=W\)。
根据 \(MRP=MFC\) 的要素需求原则,厂商面临工资水平 \(W=W_1\) 为常数,因此劳动雇佣数量为 \(L=L_2\),小于完全竞争市场的劳动雇佣数量 \(L_1\)。
(五)买方垄断厂商的要素需求
买方垄断厂商面临完全竞争的产品市场、不完全竞争的要素市场,此时:\(MRP=VMP\),\(MFC>W\)。
1. 买方垄断的特点
- 厂商具有要素价格决定权;
- 厂商对要素价格的决定收到要素供给曲线的制约;
- 要素价格越高,要素供给量也越高;
- 边际要素成本大于要素价格:\(MFC>W\)
2. 买方垄断厂商的要素需求
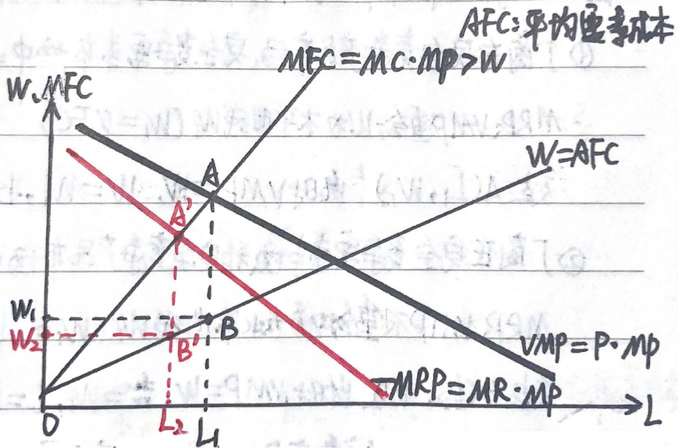
如图所示,根据 \(MRP=MFC\) 的要素需求原则,厂商在 \(A\) 点雇佣劳动数量为 \(L_1\),此时工资水平为 \(W_1\)。买方垄断(厂商垄断)要素市场时,厂商只支付劳动力最低能接受的工资水平 \(W_1\)(\(B\) 点)。
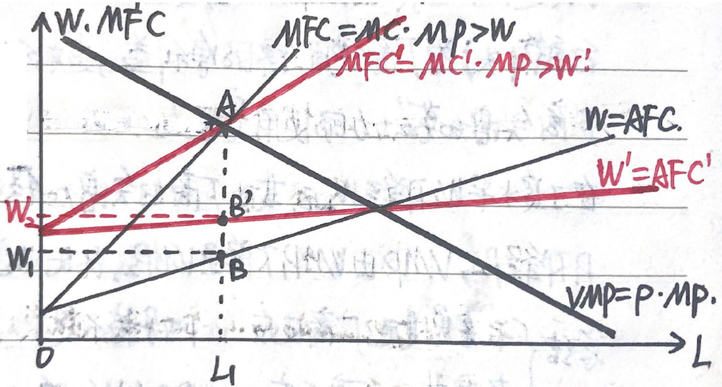
(六)买卖垄断厂商使用的要素需求
买卖垄断厂商面临不完全竞争的产品市场与要素市场,此时:\(MRP<VMP\),\(MFC>W\)。
如图所示,根据 \(MRP=MFC\) 的要素需求原则,确定 \(A'\) 点的劳动雇佣数量为 \(L_2\),此时工资水平为 \(W_2\)。厂商垄断产品市场与要素市场时,只愿意支付最低能接受的工资水平 \(W_2\)(\(B'\) 点)。
与"完全竞争厂商"的均衡点 \(A\) 点 \(L_1\) 的劳动雇佣数量与 \(W_1\) 的工资水平相比,\(L_2 < L_1\),\(W_2 < W_1\)。
三、生产要素的供给
在此关于要素供给的讨论完全局限于要素所有者为消费者、其行为目的为效用最大化这一范围之内,即是从消费者的效用最大化行为出发来建立其要素供给量与要素价格之间关系的理论。
(一)要素供给的特点与原则
1. 要素供给的特点
- 生产要素供给有限
- 供给量取决于机会成本
2. 要素供给的原则:效用最大化
2.1 效用最大化
在一定时期,要素的所有者所拥有的全部生产要素的数量是一定的,要素供给可以看成是“要素供给”和“保留自用”两种用途上进行分配以获得最大效用。要想效用最大化,就是使供给要素的边际效用和保留自用的边际效用相等。
2.2 要素供给的边际效用
生产要素对消费者的效用属于“间接效用”,它是通过收入而与效用相联系:
\[ \begin {align} \frac {d U} {dL}=\frac {dU} {dY} \cdot \frac {dY} {\Delta L} \end {align} \]
考虑到完全竞争的要素市场,要素的边际收入等于要素的价格,因此:
\[ \begin {align} \frac {d U} {dL}=\frac {dU} {dY} \cdot W \end {align} \]
2.3 自用资源的边际效用
为了使分析简单化,假定自用资源的效用都是直接的。若用 \(l\) 表示自用资源数量,则自用资源的边际效用为 \(\frac {d U} {dl}\),它表示增加一单位自用资源所带来的效用增量。
对于劳动力供给而言,如果劳动力在闲暇与工作之间分配劳动时间,那么:
- 闲暇的边际效用:\(MU_H= \frac {\partial U} {\partial H}\),表示每增加一单位闲暇时间所增加的总效用;
- 工作的边际效用:\(MU_Y = \frac {\partial U} {\partial Y}\),表示每增加一单位工作时间所增加的总效用。
2.4 要素供给原则
对于消费者而言,要素供给的目的是实现效用最大化。
借助于要素供给的间接效用和自用资源的直接效用概念以及所谓“收入的价格”\(W_y\),效用最大化条件表示为:
\[ \begin{align} \frac {dU/dl} {dU/dY}=\frac W {W_y} \end{align} \]
要素供给原则也可以用数学方法予以推导,约束条件为:
\[ \begin{align} Y+W \cdot l = W \cdot {\overline L} \end{align} \]
效用函数为 \(U=U(Y,l)\) 最大化,可构造拉格朗日辅助函数为:
\[ \begin{align} f = U(Y,l) + \lambda \big (Y+W \cdot l - W \cdot {\overline L} \big) \end{align} \]
3. 无差异曲线分析
消费者现在的问题是:在预算约束之下选择最优(效用最大)的收入 \(Y\) 和自用资源 \(l\) 的组合。这个最优组合是预算线与无差异曲线 \(U_1\) 的切点 \(G^*\),满足 \(\frac {dU} {dl}=W\)。
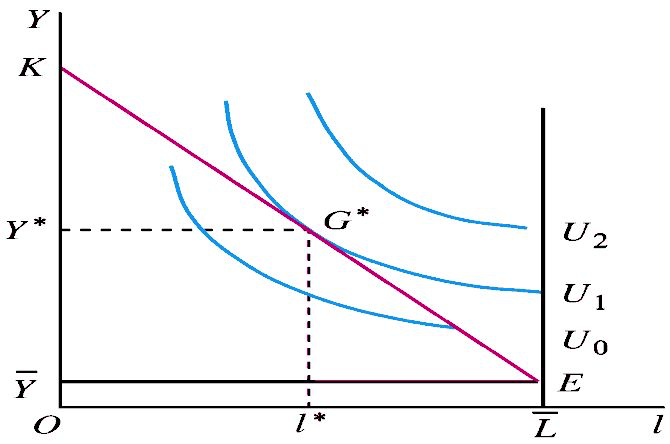
4. 要素供给问题
如下图所示,随着要素价格的变动,可得价格扩展线 \(PEP\)。
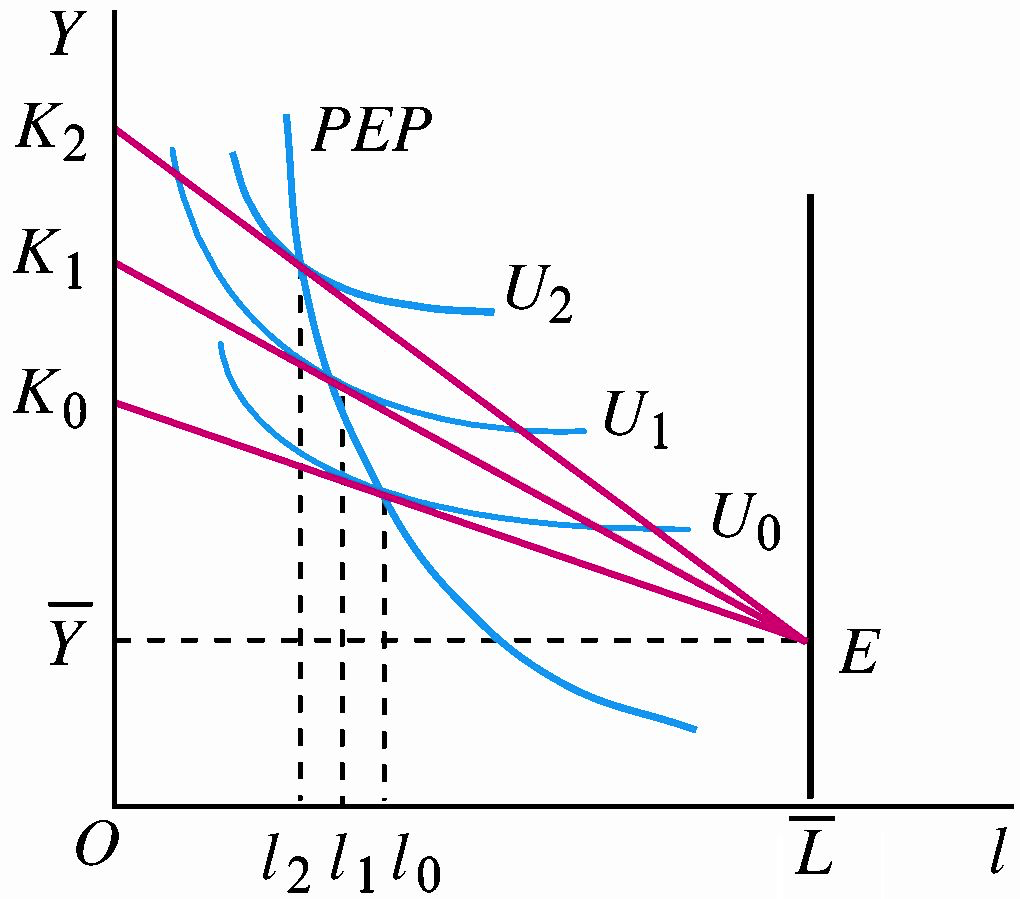
由上图可以推导出下图的要素供给曲线。
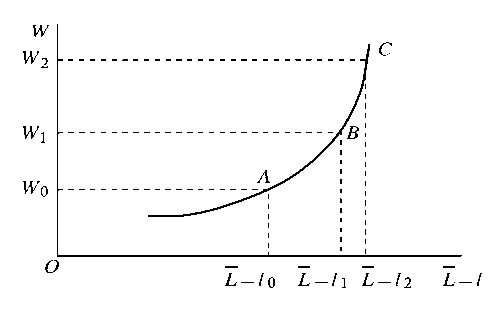
一般情况下,要素供给曲线具有向右上方倾斜的正斜率性质。但是,并不是所有的要素供给曲线都总是向右上方倾斜的,要素供给曲线与要素的特点息息相关,呈现出不同的形状。
(二)劳动供给曲线和工资率的决定
1. 劳动供给曲线
劳动供给曲线呈现向后弯曲的特点。
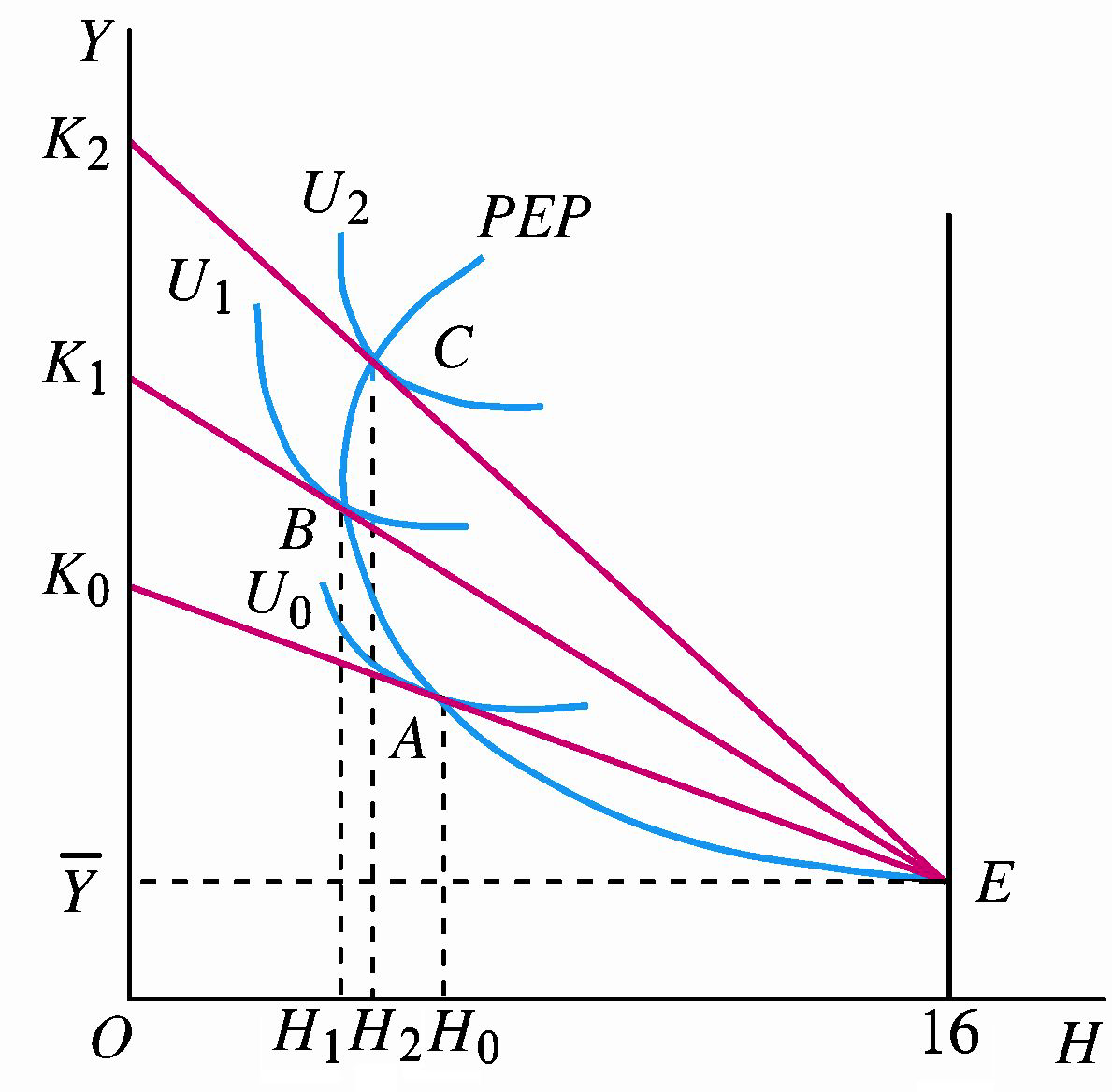
让工资连续变化 \(W_0 \to W_1 \to W_2 \to …\), 便得到下图的劳动供给曲线,具有向后弯曲的特点。
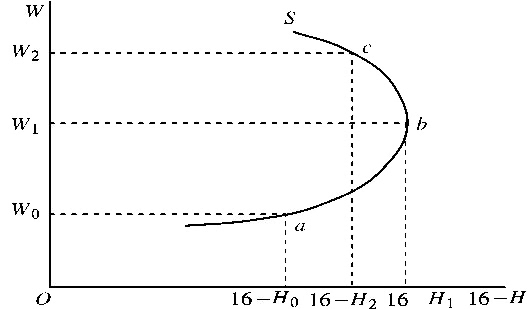
2. 替代效应和收入效应
假定工资上涨:
- 替代效应:由于工资上涨,闲暇变得更加“昂贵”,消费者会减少对它的“购买”,从而提供的劳动数量增加。
- 收入效应:由于工资上涨,意味着实际收入上升。随着实际收入上升,消费者会增加对闲暇需求,从而提供的劳动数量减少。
- 当收入效应小于替代效应时,劳动供给则会随着工资率的提高而增加,劳动供给曲线向右上方倾斜,即曲线斜率为正值。当收入效应大于替代效应时,劳动供给量则可能随着工资率的提高而减少,劳动供给曲线向左上方倾斜,即曲线斜率为负值。
- 工资率较低时,替代效应大于收入效应;工资率很高时,收入效应大于替代效应。随着工资率的提高,劳动供给曲线会从向右上方倾斜转为向左上方倾斜。
3. 劳动的市场供给曲线和均衡工资的决定
市场劳动供给曲线向右上方倾斜。向右下方倾斜的劳动需求曲线和向右上方 倾斜的劳动供给曲线决定均衡工资水平。

(三)资本的供给曲线
1. 资本供给曲线
资本的供给量指家庭储蓄的那部分资金。
资本的供给曲线是储蓄量与利率之间关系的曲线,随着利率的不断升高,资本供给量先升高后降低。
2. 形成原因
消费者的跨期选择的结果
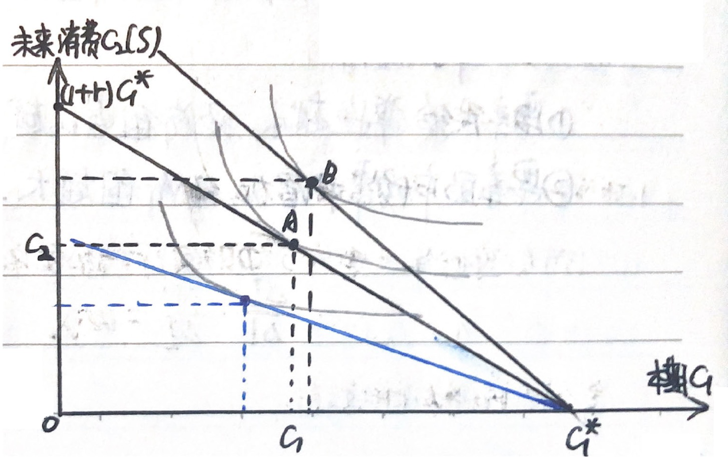
3. 利率对资本供给的影响
上图的斜率为 \(k=1+r\),因此:
- 当利率升高(\(A \to B\))时,本期消费 \(C_1\) 升高,未来消费(储蓄/资本供给)\(C_2\) 下降,但由于利率 \(r\) 升高,导致未来的实际消费会上升。
- 利率可以看作为现期消费的价格。

(四)土地的供给曲线和地租的决定
1. 土地供给曲线
与劳动力一样,土地所有者实际上是在土地供给所可能带来的收入与自用土地之间进行选择,其效用函数可以写为:\(U=U(Y,q)\)。由于通常土地的消费性使用可以忽略不计,故效用只取决于土地收入而与自用土地数量大小无关。
因此,土地所有者为了获得最大效用就必须使土地收入达到最大,而要土地收入最大则必须要求尽可能地多供给土地。由于土地所有者拥有的土地为既定的,单个土地供给者提供的土地通常只有一种用途,从而土地供给无弹性,在图形中表现为一条垂直于横轴的直线。
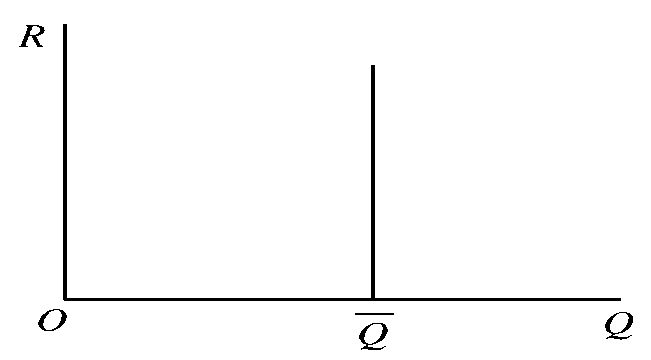
2. 地租的决定
向右下方倾斜的土地市场需求曲线与土地供给曲线结合起来可决定土地的均衡价格即地租。而且,地租完全由土地的需求曲线决定。
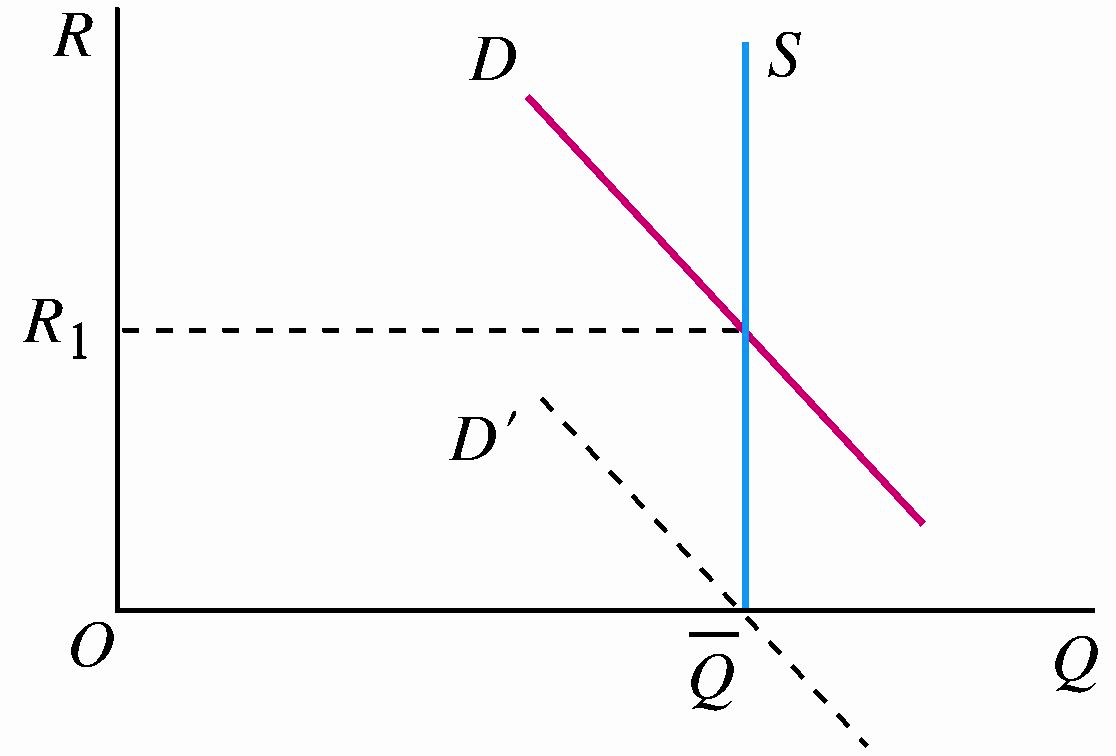
(五)租金、准租金和经济租金
(传送门:"不同成本、利润之间的关系")
1. 租金(Rent)
供给数量同样固定不变的一般资源,如某些人的天赋才能,其服务价格称之为租金。换句话说,地租是当所考虑的资源为土地时的租金,而租金则是一般化的地租。
2. 准租金(Quasi-rent)
准租金是对供给量暂时固定的生产要素的支付,即固定生产要素的收益。因此,准租金属于短期分析。
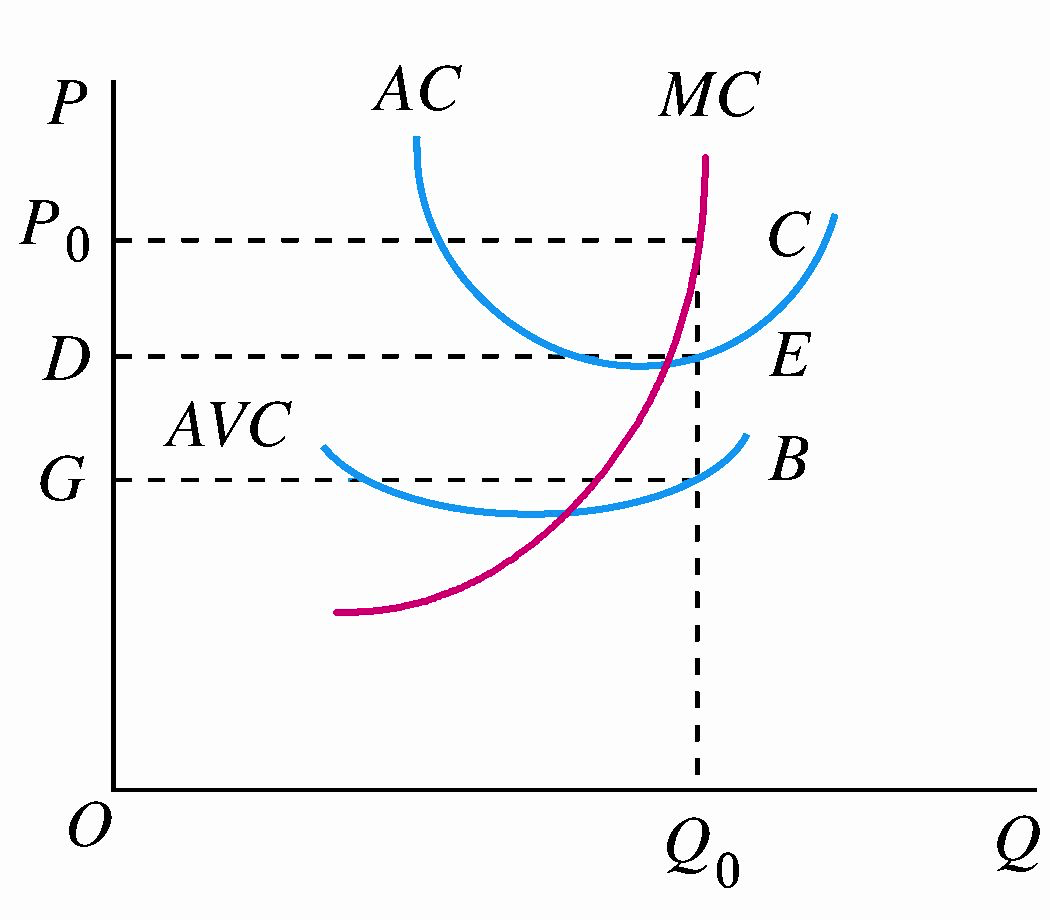
可变成本为面积 \(OGBQ_0\),它代表了厂商对为生产 \(Q_0\) 所需的可变生产要素量而必须作出的支付。固定要素得到的则是剩余部分 \(GP_0CB\)。这就是准租金,等于总收益减去总可变成本。
如果从准租金 \(GP_0CB\) 中减去固定总成本 \(GDEB\),则得到经济利润 \(GP_0CE\)。可见,准租金为固定总成本与经济利润之和。当经济利润为 0 时,准租金便等于固定总成本。当厂商有经济亏损时,准租金也可能小于固定总成本。准租金可表示为:(传送门:"生产者剩余")
\[ \begin {align} TR-TVC=TFC+经济利润=TFC-经济损失 \end{align} \]
3. 经济租金(Economic Rent)
相对而言,经济租金属于长期分析。如图所示,要素供给曲线 \(S\) 以上、要素价格 \(R_0\) 以下的阴影区域 \(AR_0E\) 为经济租金。
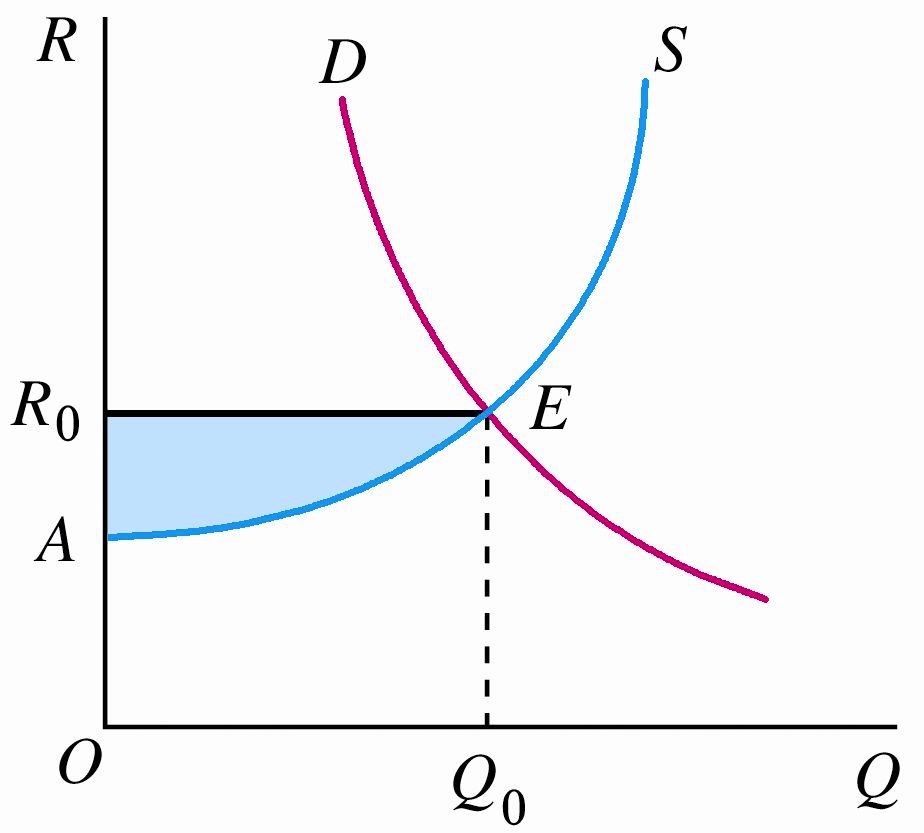
事实上,经济租金也可以这样来定义,即支付给生产要素的报酬超出为获得该要素而必须支付的最低报酬的部分。
可以发现,如果供给是完全有弹性的,经济租金将是零。只有在供给多少缺乏弹性时,经济租金才出现。在供给完全无弹性时,所有向生产要素支付的进入都是经济租金。因此,租金实际上是经济租金的一种特例。
四、洛伦兹曲线和基尼系数
(传送门:"收入-消费曲线和恩格尔系数")
(一)洛伦兹曲线
将一国总人口按收入由低到高进行排序,考虑收入最低的任意百分比人口所得到的收入百分比,将人口累计百分比和收入累计百分比的对应关系描绘在图形上,就是洛伦兹曲线。
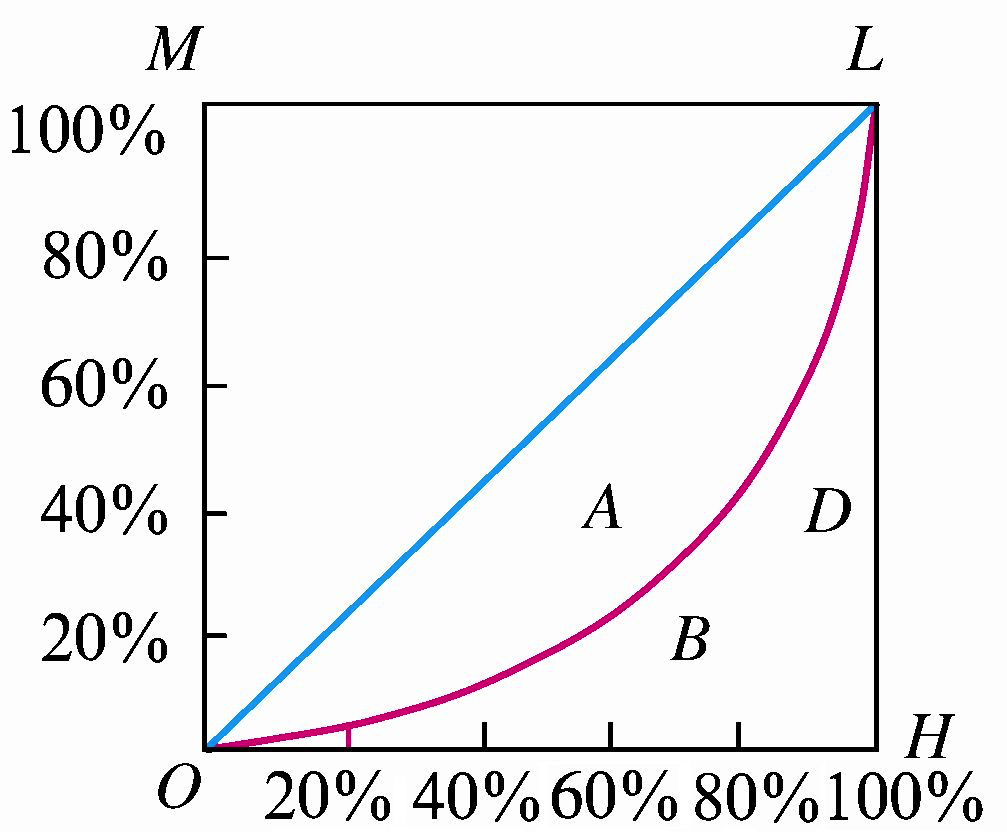
洛伦兹曲线反映了收入分配的不平等程度。曲线弯曲程度越大,收入分配程度越不平等;反之亦然。
(二)基尼系数
在洛伦兹曲线图中,不平等面积与完全不平等面积之比,称为基尼系数,是衡量一个国家贫富差距的标准。若设 \(G\) 为基尼系数,则:\(G= \frac A {A+B}\) 。
显然,基尼系数不会大于 1, 也不会小于零,即有:\(0 \le G \le1\)。
相关资源:

