实证｜为什么使用PSM消除样本选择偏差？

　　要理解为什么用 psm 消除样本的选择偏误，先要理解 psm 的原理。

　　在研究一种干预措施的效果时，理想状态是进行随机化实验，也就是控制其他所有条件都相同，仅有是否采取干预措施这一点不同，这样就可以通过比较随机化实验中干预组与对照组的差异，了解干预措施的效果，为排除个体差异，通常使用干预组与对照组的效果的平均值差异来衡量，也就是许多实证研究中许多研究计算的平均处理效应。

　　然而，随机化实验往往在医学、生物学等领域更为常见，在经济学相关研究中，经济发展情况、社会制度、文化差异等各方面的不同之处决定了不能随意指定两类样本进行比较，以衡量干预措施的效果。更多的情况是干预措施的效果会受到两组样本之间其他差异的影响，这种情况下，无法准确判断两组之间的差异是不是由这一干预措施带来的，也就是无法准确判断干预措施与结果差异之间的“因果关系”。

　　因此，为了可以更准确估计来自干预措施的影响，更准确地识别这种“因果关系”，回归的方式最早被应用，常见的是线性回归。然而，使用回归方法判断的是两个变量之间的统计关系，在需要满足 CIA（条件独立性假设）或 CMI（条件均值独立性假设）的条件下，该统计关系才可以解释为干预措施的因果关系。

什么是 CIA 假设？

　　

　　（CIA 假设比 CMI 假设更强，具体可以参见赵西亮老师的《基本有用的计量经济学》第 5 章第 2 节）

　　然而，这种回归的方式也有缺陷。一是回归方式不能解决在样本抽样阶段造成的选择性偏误；二是由于数据的可得性，往往实证研究中并不能做到饱和回归，许多变量对结果的影响无法被观测到。因此，在实际上，回归的方式也难以满足CIA条件，难以得到准确的“因果效应”。

什么是PSM？为什么PSM？

　　PSM是倾向得分匹配，其本质是构造一个倾向得分，通过比较倾向得分，匹配干预组与对照组，构造出一个“准自然实验”，因此，PSM在理论上比回归的方法更有可能满足CIA条件。

　　PSM的估计过程大体可以分为以下4个步骤（参考赵西亮老师的《基本有用的计量经济学》）：

1. 定义相似性

　　为了准确估计因果效应，需要找到其他条件都相似的干预组与对照组，因此需要定义相似性。相似性的定义，需要关注哪些变量应当作为定义相似性的依据，以及如何测度相似性。

　　对于变量的选择上，定义相似性的变量应当满足CIA条件，也就是控制了这些变量后，干预组与控制组不能有其他未观测到的差异。

　　

　　

　　对于如何测度相似性：一般采用马氏距离或欧氏距离

　　

　　

　　

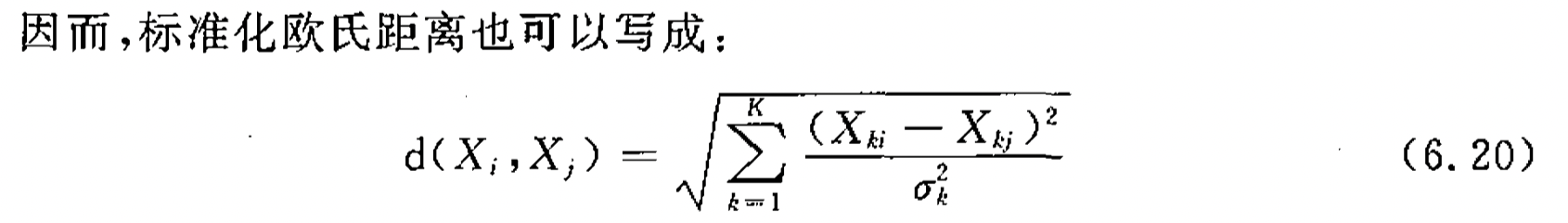
　　那么，就可以通过logit回归等方式估计需要的倾向得分：

　　

2. 实施匹配

　　在实施匹配的方法上，主要有近邻匹配和分层匹配两种形式。

　　近邻匹配包括一对一匹配与一对多匹配。

　　

　　而分层匹配则是根据倾向得分的取值，对样本进行分层，以减小每一层内的倾向得分的差距，获得更好的匹配效果。

　　

3. 匹配效果诊断

　　匹配效果好不好，主要取决于干预组与对照组的控制变量差异是否得到了有效控制。在实证中，具体体现为控制变量的平衡性检验。

　　CIA假设是因果关系识别的关键。虽然CIA假设难以被验证成立，但证明CIA不成立却相对简单。如果实施匹配后控制变量的平衡性检验无法通过，则说明CIA不成立，使用当前匹配方法估计出的因果效应不是真实的干预措施因果效应的可能性较大。

　　

4. 因果效应估计

　　在通过了匹配效果的检验后，因果效应的估计才是可靠的。在最后一步，再估计干预措施的因果效应。

当然，PSM也有问题：

　　基于几个控制变量测度出的倾向得分，难以包含不可测因素的影响，PSM难以避免不可测因素对结果的影响。在经济学相关的研究中，最常见的是讨论某个经济干预行为对另一个经济因素的影响，但由于制度因素相对更难度量，制度因素的缺失可能导致估计出的经济干预行为的效果有偏差。

　　为解决这一问题，也有使用工具变量法、使用面板数据等方式，更进一步进行估计。