技术变化的倾向和替代弹性，决定资本-劳动比率（\(K/L\)）和工资-租金比率（\(w/r\)）之间的关系，进而决定劳动和资本的收入份额。

　　技术变化通常根据使用生产要素的倾向分类。希克斯分类 (John Hicks, 1932)，以特定资本-劳动比率下劳动和资本的边际替代率的变化方向为基础。

　　假设 \(i\) 为等产量线)，可以表示为：\(I=F(L,K)\)。等产量线向原点移动 \(i_0 \to i_1\) 表示技术进步，因为技术进步意味着生产单位产出需要的投入要素更少。

1. 要素收入份额的图形分析

　　如下图所示，\(i\) 为等产量曲线，\(PQ\) 为等成本曲线，两者相切于 \(a\) 点，即为既定产量下最低成本的均衡。

　　资本与劳动的收入份额

　　假设等成本线：\(C=wL+rK\)，那么 \(Q\) 点坐标 \((0, \frac C r)\)，\(P\) 点坐标 \((\frac C w, 0)\)。因此直线 \(PQ\) 的斜率绝对值为 \(\frac w r\)，即 \(\frac {aT} {TP} = \frac w r\)。

　　此时处于均衡状态，因此 \(a\) 点坐标即为均衡时的劳动、资本投入量 \((L,K)\)，过原点 \(O\) 的直线 \(Oa\) 斜率为 \(\frac K L\)，为资本-劳动比率，即 \(\frac {aT} {OT}=\frac K L\)。

\[ \begin{align} \frac {TP} {OT} = \frac {aT/OT} {aT /TP} = \frac { rK} {wL} \end{align} \]

　　因此，\(\frac {TP} {OT}\) 的取值，即为资本收入和劳动收入的相对份额，该数值越大，资本收入的份额越大、劳动收入份额越小。

　　在两要素经济中，希克斯的技术变化可以分为三种类型。

2. 希克斯中性技术进步

　　中性技术进步：对于特定的资本-劳动比率 \(K/L\)，技术进步不改变劳动和资本的边际产出的比率 \(F_L / F_K = {w} / {r}\)。

中性技术进步

　　如图所示：等产量线移动 \(i_0 \to i_1\) 表示技术进步。

　　劳动和资本的边际生产率为边际技术替代率（marginal ratio of technical substitution）：

\[ \begin{align} MRTS_{LK} = \frac {\partial K} {\partial L} = \frac {F_L} {F_K} \end{align} \]

　　其中，\(MRTS_{LK}\) 即为等产量线 \(i\) 的切线斜率的绝对值。由原点发出的射线 \(OA\) 与两条等产量线 \(i_0\)、\(i_1\) 分别相交于点 \(a\)、点 \(b\)，且两点处等产量线的斜率相同，因此为希克斯中性的技术进步。

　　希克斯中性的技术进步表明，技术进步不改变各要素的边际产出，因此不会改变各要素的边际替代关系 \(MRTS_{LK}\)。

　　在均衡的竞争性要素市场中，劳动 \(L\) 和资本 \(K\) 的边际技术替代率 \(MRTS_{LK}\) 等于工资与租金比率，即 \(MRTS_{LK} = {w} / {r}\)。如果资本-劳动比率不变，技术进步就是中性的。此时，劳动收入 \(wL\) 与资本收入 \(rK\) 的比率不变，意味着劳动和资本之间的收入份额不变。

　　结合图解，若在上图中作出两条过 \(a\) 与 \(b\) 点的垂线，交横轴于 \(T_a\) 与 \(T_b\)，那么可以得到 \(\frac {T_aP_0} {OT_a} = \frac {T_bP_1} {OT_b}\)，即劳动收入份额与资本收入份额都不发生改变。

3. 希克斯劳动节约型技术进步

　　劳动节约型技术进步：对于特定的资本-劳动比率 \(K/L\)，技术进步会减小劳动和资本的边际产出的比率 \(MRTS_{LK} = F_L / F_K = {w} / {r}\)，等成本线发生非平行移动，此时，劳动的边际产出 \(F_L\) 下降，资本的边际产出 \(F_K\) 升高，应该减少劳动投入，增加资本投入。

劳动节约型技术进步

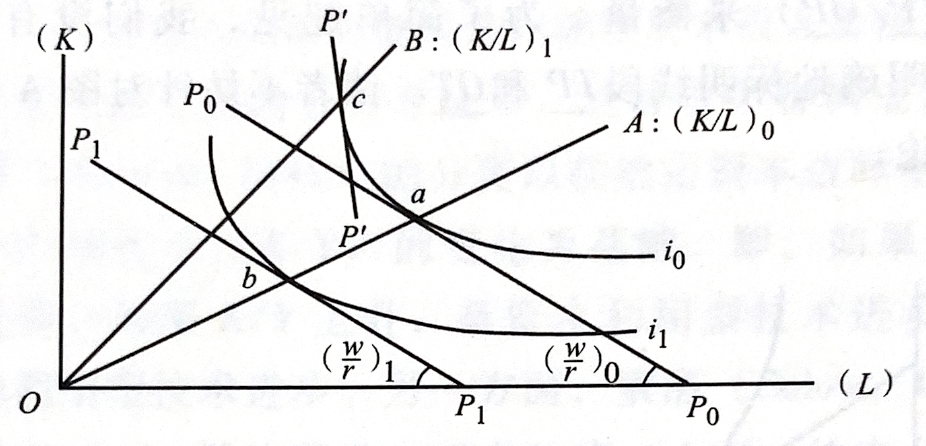
　　特征：资本-劳动比率 \(K/L\) 越高，即切点与原点的连线越陡峭（比较 \(OA\) 线与 \(OB\) 线），等产量线向原点移动幅度越大。

　　结果：随着技术进步 \(i_0 \to i_1\)：

  • 对于固定 \(K/L\) 比率的 \(OA\) 线，其交点由 \(a\) 移动到 \(b\)，此时切点斜率下降，即劳动与资本的边际产出比率 \(F_L / F_K\) 下降。
  • 对于固定 \(w/r\) 比率的 \(OB\) 线，其交点由 \(a\) 移动到 \(c\)，\(K/L\) 比例提升。

　　希克斯劳动节约型技术进步可以被定义为对于给定 \(w/r\) 诱发 \(K/L\) 比例提高的技术进步，资本收入份额的增加是以牺牲劳动收入份额下限为代价的。

　　结合图解，若在上图中作出两条过 \(a\) 与 \(b\) 点的垂线，交横轴于 \(T_a\) 与 \(T_b\)，那么可以得到 \(\frac {T_aP_0} {OT_a} \lt \frac {T_bP_1} {OT_b}\)，即资本收入份额相对侵占了劳动收入份额。

4. 希克斯资本节约型技术进步

　　资本节约型技术进步：对于特定的资本-劳动比率 \(K/L\)，技术进步会增大劳动和资本的边际产出的比率 \(MRTS_{LK} = F_L / F_K = {w} / {r}\)，等成本线发生非平行移动，此时，劳动的边际产出 \(F_L\) 升高，资本的边际产出 \(F_K\) 下降，应该增加劳动投入，减少资本投入。

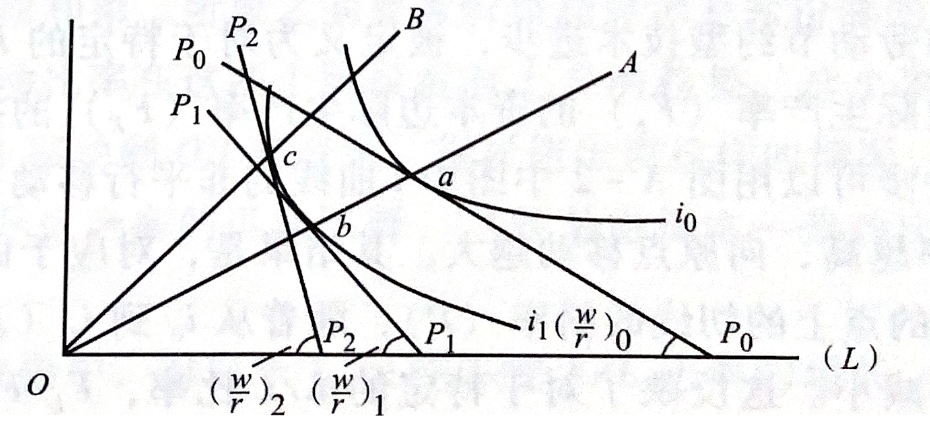
资本节约型技术进步

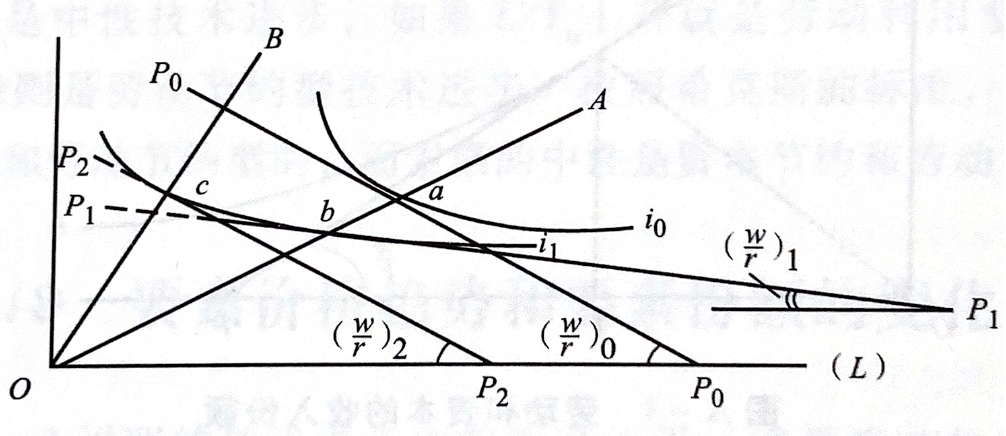
　　特征：资本-劳动比率 \(K/L\) 越低，即切点与原点的连线越陡峭（比较 \(OA\) 线与 \(OB\) 线），等产量线向原点移动幅度越大。

　　结果：随着技术进步 \(i_0 \to i_1\)，对于固定 \(K/L\) 比率的 \(OA\) 线，其交点由 \(a\) 移动到 \(b\)，此时切点斜率变大，即劳动与资本的边际产出比率 \(F_L / F_K\) 变大。

　　希克斯资本节约型技术进步可以被定义为对于给定 \(w/r\) 诱发 \(K/L\) 比例下降的技术进步，劳动收入份额的增加是以牺牲资本收入份额为代价的。

　　结合图解，若在上图中作出两条过 \(a\) 与 \(b\) 点的垂线，交横轴于 \(T_a\) 与 \(T_b\)，那么可以得到 \(\frac {T_aP_0} {OT_a} \gt \frac {T_bP_1} {OT_b}\)，即劳动收入份额相对侵占了资本收入份额。

补充：其他技术进步分类方式：

哈罗德 (Harrod, 1948) ：以资本边际生产率 \(w\) 表示的资本产出比率 \(K/Y\) 的变化为基础

  1. 中性技术进步：\(K/Y\) 保持不变
  2. 资本节约型技术进步：\(K/Y\) 下降
  3. 劳动节约型技术进步：\(K/Y\) 上升

索洛 (Solow, 1970) ：以工资率 \(w\) 表示的劳动产出比率 \(L/Y\) 的变化为基础

  1. 中性技术进步：\(L/Y\) 保持不变
  2. 资本节约型技术进步：\(L/Y\) 上升
  3. 劳动节约型技术进步：\(L/Y\) 下降

三种技术进步分类方式的关系：

  1. 哈罗德中性 \(\Rightarrow\) 希克斯劳动节约型
  2. 索洛中性 \(\Rightarrow\) 希克斯资本节约型