微观|第9章:一般均衡论与福利经济学
【内容速查与目录】
【笔记下载】
一、一般均衡论
(一)局部均衡和一般均衡
1. 局部均衡
局部均衡是指在假设其他市场不变的情况下,某一特定产品或要素的市场均衡。局部均衡分析研究的是单个(产品或要素)市场,其研究方法是把所考虑的某个市场从相互联系的整个经济体系的市场全体中“取出”来单独加以研究。
2. 一般均衡
一般均衡是指在一个经济体系中,所有市场的供给和需求同时达到均衡的状态。一般均衡论所考察的问题是:在社会上各种产品的交易市场是相互联系、相互影响的背景下,最后各种自发的经济活动是否趋于供求均衡?
(二)一般均衡的存在性
研究证明,在一定的假设条件全部得到满足时,一般均衡体系就有均衡解存在。
(三)一般均衡的实现“试探过程”
关于论证一般均衡的实现,瓦尔拉斯假设采用的是“试错法”,即在市场中存在一个自由拍卖人,其任务就是寻找并确定能与市场供求一致的均衡价格。
二、经济效率
(一)实证经济学和规范经济学
实证经济学(Positive Economics)回答“是什么”、“为什么”和“会如何”的问题,研究实际经济体系是怎样运行的。它对经济行为作出有关的假设,根据假设分析和陈述经济行为及其后果,并试图对结论进行检验。
规范经济学(Normative Economics)回答“应当是什么”的问题, 根据一定的社会价值判断标准,对一个经济体系的运行进行评价,并进一步说明一个经济体系应当怎样运行,以及为此提出相应的经济政策。
比如,尽管知道存在一般均衡,但这种一般均衡状态是否对整个社会是“最优”的呢?
(传送门:"规范分析和实证分析")
(二)福利经济学
福利经济学是在一定的社会价值判断标准条件下,研究整个经济的资源配置与个人福利的关系,特别是市场经济体系的资源配置与福利的关系,以及与此有关的各种政策问题。
(三)帕累托最优状态:经济效率
福利经济学采用帕累托最优标准来衡量资源配置的最优配置。
帕累托最优状态(Pareto efficiency)是这样一种状态:任何改变都不可能使一个人的境况变好,而又不使别人的境况变坏。当经济系统达到帕累托最优状态时,经济运行是有效率的;反之,不满足帕累托最优状态的经济运行结果就是缺乏效率的。
如果对既定资源配置的状态予以改变,而这种改变使得至少有一个人的境况变好,同时其他人的境况没有因此变坏,则认为这种变化增加了社会福利,或称帕累托改进。
三、帕累托最优条件
(一)交换的帕累托最优条件
交换的一般均衡(general equilibrium of exchange)是指在社会生产产量状况和收入分配状况既定条件下,通过产品的交换使得交换者达到效用之和最大化的均衡状态,此时实现交换的帕累托最优。
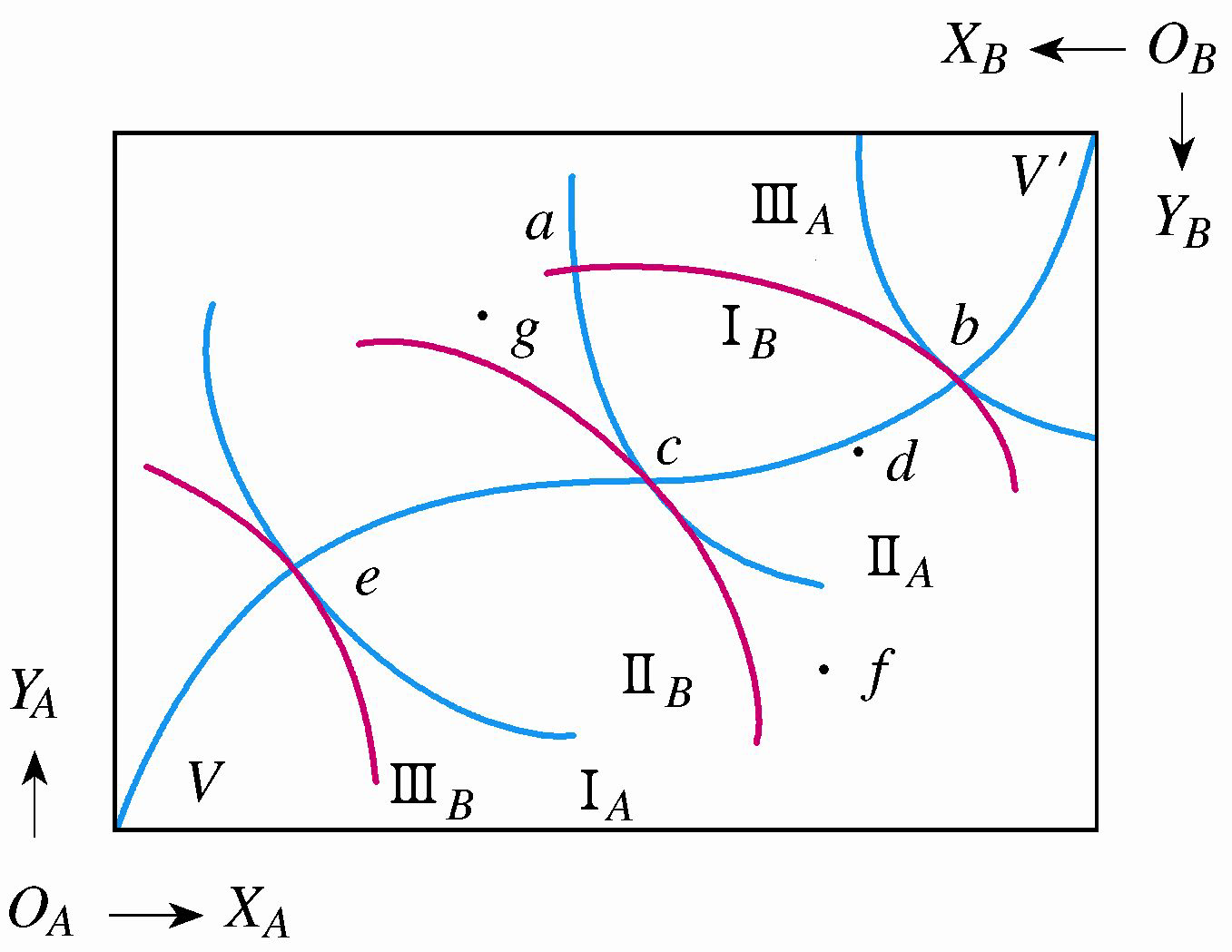
如图所示,任何一点,如 \(a\) 点,对应于消费者 \(A\) 的消费量 \((X_A ,Y_A)\) 和消费者 \(B\) 的消费量 \((X_B , Y_B )\),都有下式成立:
\[ \begin {align} X_A+X_B=\overline X \\ Y_A+Y_B=\overline Y \end {align} \]
即埃奇渥斯盒状图中的任意一点都表示两种商品在消费者 \(A\) 和 \(B\) 之间的分配。
- 埃奇渥斯盒状图中的任意一点要么处于 \(A\) 和 \(B\) 的无差异曲线的交点上,要么处于他们的切点上。
- 上图中, \(a\) 点不能代表帕累托最优状态,因为存在帕累托改进。当然,这种改进的途径不是唯一的。
- \(e\) 点、\(c\) 点和 \(b\) 点等类似的点都是帕累托最优状态的点。
- 把代表帕累托最优状态的点连接起来,就成了交换的契约曲线,在图中用 \(VV'\) 表示。当然, \(VV'\) 曲线上任一点,比如 \(b\) 点和 \(c\) 点,无法按照帕 累托标准予以比较,只能根据社会分配的偏好选择其中的某些状态。
- 由此可得"商品交换的帕累托最优条件":两种商品的边际替代率相等,即 \(MRS_{XY}^A = MRS_{XY}^B\)
(二)生产的帕累托最优条件
生产的一般均衡(general equilibrium of production)是指在技术与社会生产资源总量既定的情况下,社会对于资源的配置使得产品产量达到最大的均衡状况,即实现生产的帕累托最优。
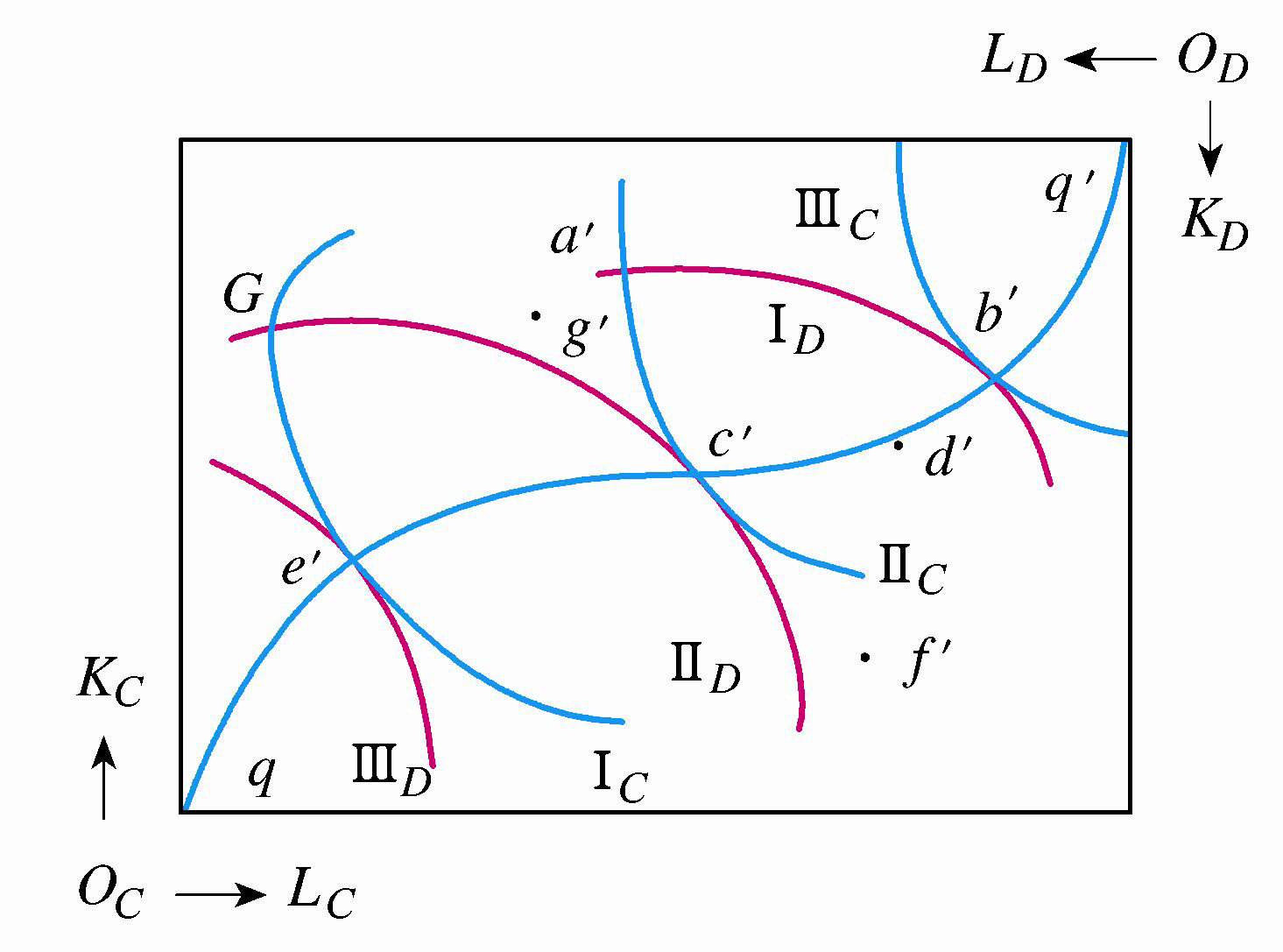
- 类似交换中的分析,这里仍采用埃奇渥斯盒状图,只是这里不用无差异曲线,而是引用等产量曲线;作为分配的商品,这里改为生产要素。
- 诸如 \(e'\)、 \(c'\) 和 \(b'\) 等满足帕累托最优的点组成的轨迹,称为“生产的契约曲线(或效率曲线)”,在图中用 \(qq'\) 表示。
- "生产(要素配置)的帕累托最优条件"的公式:\(MRTS_{LK}^C = MRTS_{LK}^D\),即任何两种生产要素之间的边际技术替代率对任何使用这两种生产要素的两个生产者来说都必须相等。
(三)交换和生产的帕累托最优条件
1. 从生产契约曲线到生产可能性曲线
生产契约曲线上的每一点表示了一定量投入要素在最优配置时所能生产的一对最优的产出,从而代表了两种产品的产量。因而,生产契约曲线上的每一点便与生产可能性边界上的每一点对应。
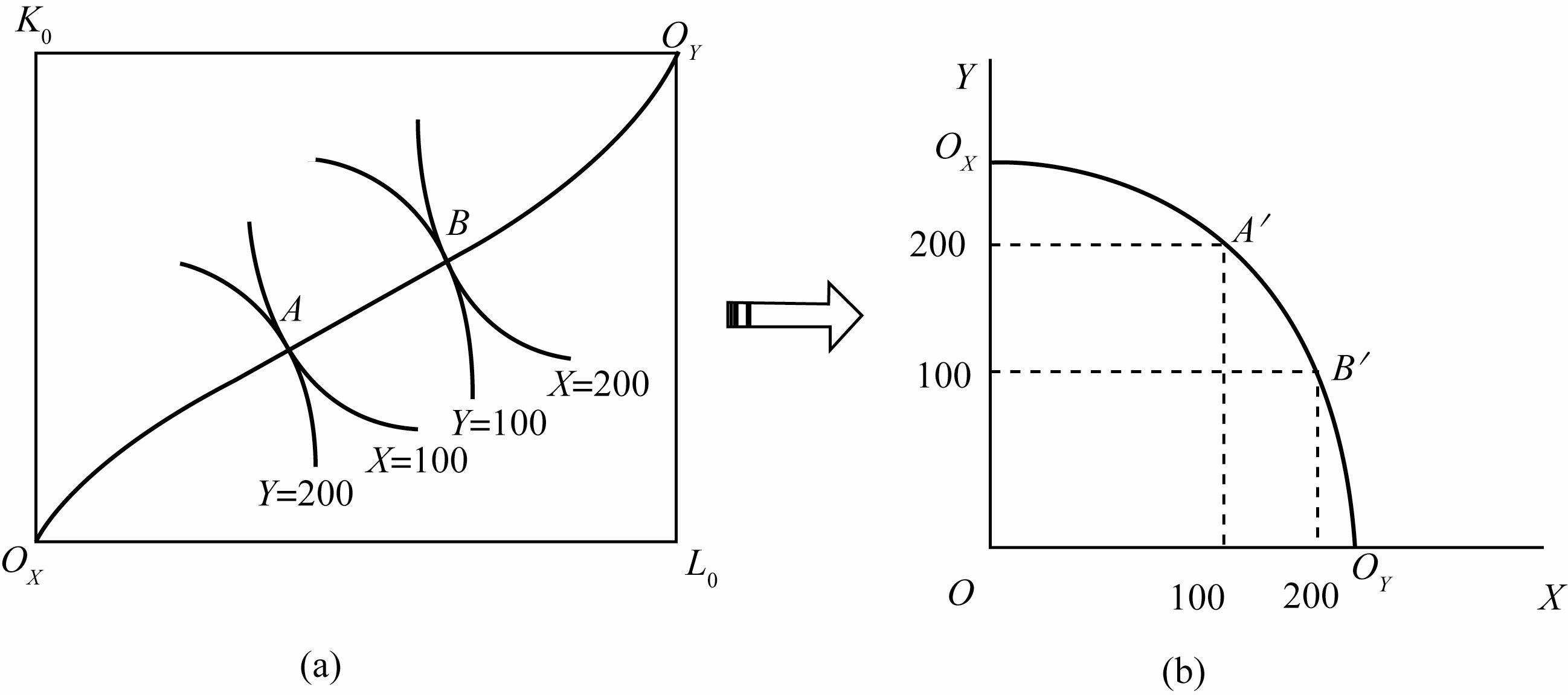
2. 生产可能性曲线
生产可能性曲线又称之为生产可能性边界(production-possibility frontier),也称之为产品转换曲线,是指在其他条件(如技术、要素供给等)不变情况下,一个社会用其全部资源所能生产的各种产品的最大数量的组合。
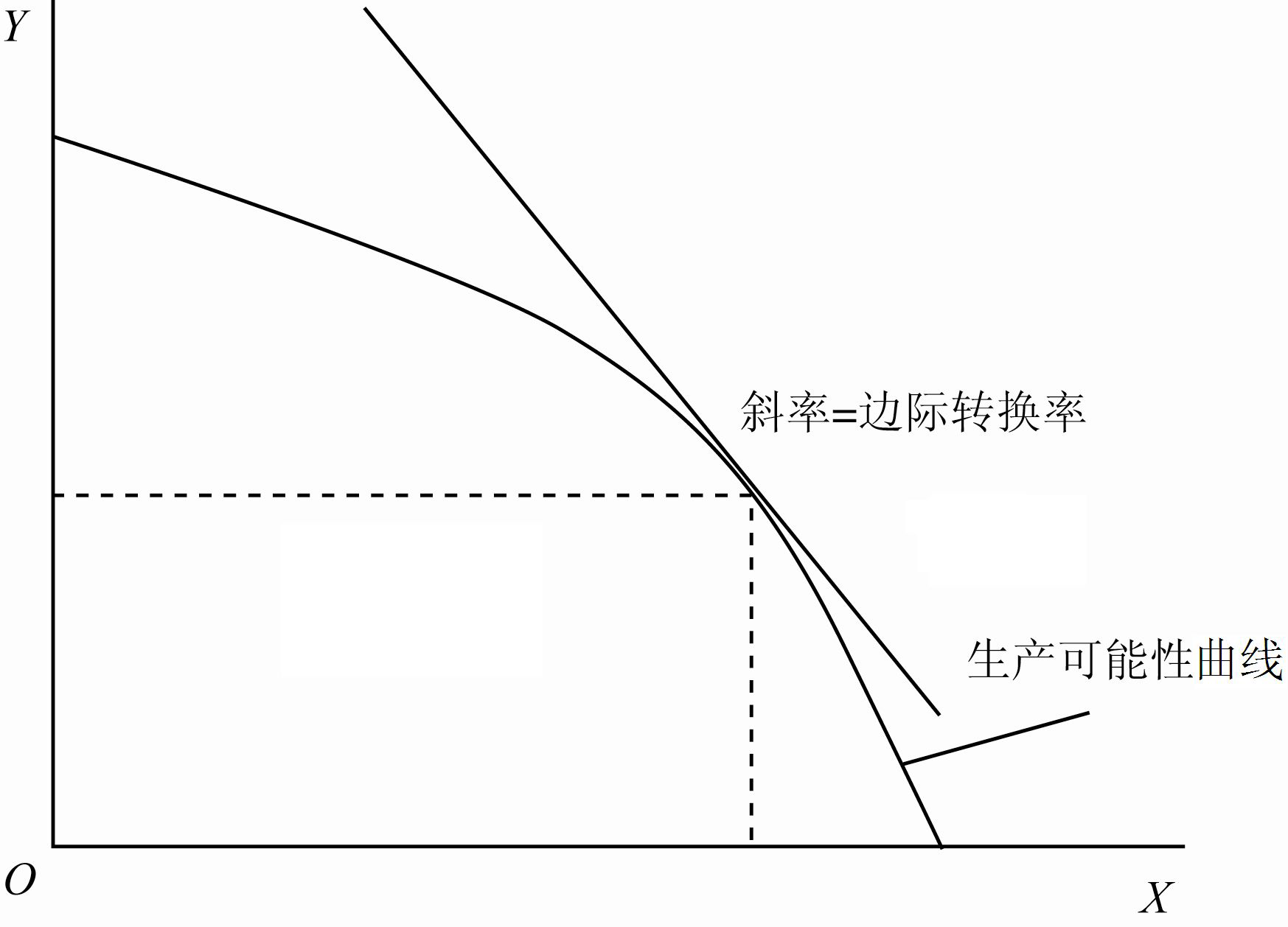
2.1 生产可能性曲线的特点
第一,生产可能性曲线的斜率为负,向右下方倾斜。生产可能性曲线斜率的极限可定义为 X 商品对 Y 商品的边际转换率(marginal rate of transformation),即生产可能性边界上每一点斜率的量值,故有:
\[ \begin {align} MRT_{XY} = \lim_{\Delta X \to 0} \left | \frac {\Delta Y} {\Delta X} \right| = \left| \frac {dX} {dY} \right| \end{align} \]
第二,生产可能性曲线凹向原点,凸向右上方,即边际转换率 MRT 是递增的。 MRT 递增的原因是要素的边际报酬递减规律。这一原因,可从如下公式看出:
\[ \begin {align} MRT_{XY} = \left| \frac {dY} {dX} \right| = \left | \frac {d Y} {d(L+K)} \cdot \frac {d(L+K)} {dX} \right| = \left | \frac { {d Y} /{d(L+K)} } { {dX} /{d(L+K)}} \right| \end{align} \]
第三,边际转换率 \(MRT_{XY}\) 等于两种产品的边际成本之比,即有:
\[ \begin {align} MRT_{XY} = \left| \frac {dY} {dX} \right| = \frac {MC_X} {MC_Y} \end {align} \]
补充:
上面计算中跳过了一个步骤,商品供给量\(Y\)与要素供给量\((L+K)\)不能直接构建联系:
\[ \begin{align} \frac {dY} {d(L+K)} = \frac {dY} {d TC } \cdot \frac {d TC } {d(L+K)}= \frac 1 {MC_Y} \cdot \frac {d TC } {d(L+K)} \end{align} \]
同理,商品供给量\(X\)于要素供给量\((L+K)\)也不能直接构建起联系。多出的\(\frac {d TC } {d(L+K)}\)在计算过程中被消除了。
2.2 生产可能性曲线的变动
如果投入要素数量或者技术状况发生了改变,则生产可能性曲线的位置就可能发生变化。
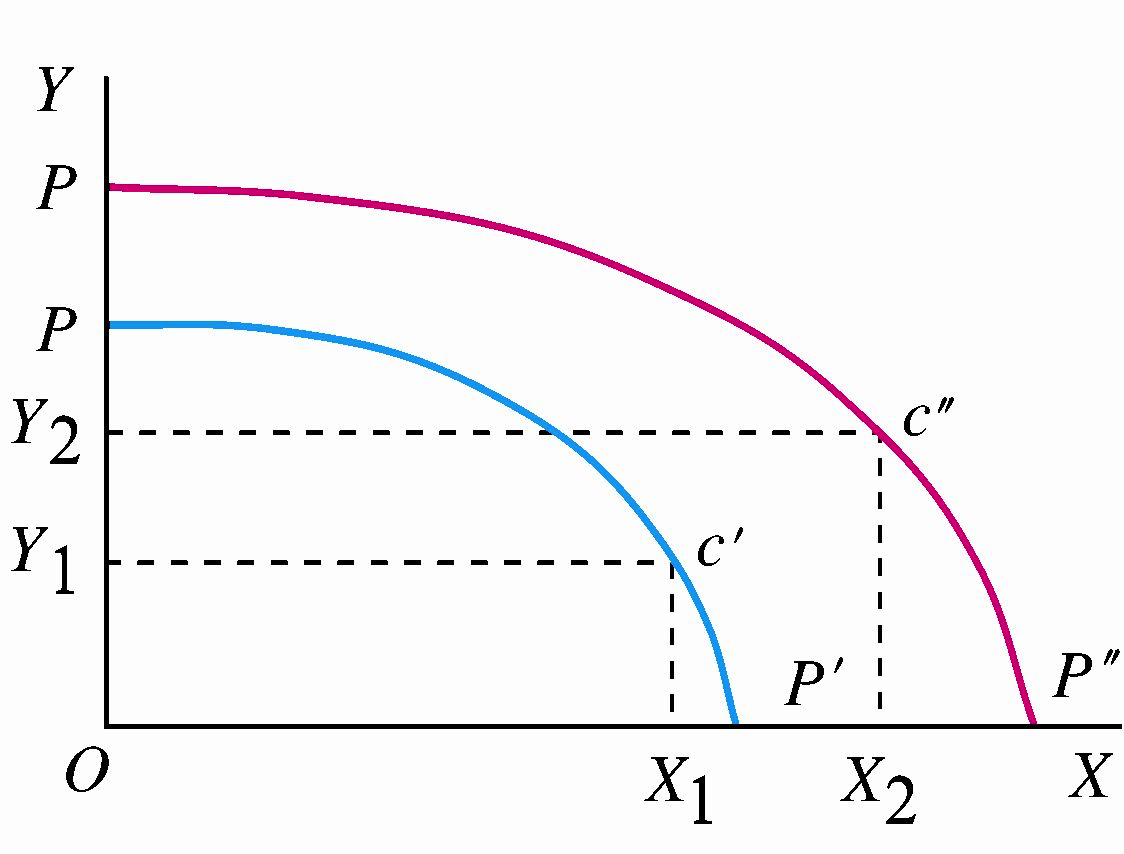
3. 生产和交换的帕累托最优条件
交换和生产的一般均衡(general equilibrium of exchange and production)是指社会生产和交换同时达到均衡的状况,即实现了交换和生产的帕累托最优状况。
生产达到均衡并不能保证交换同时达到均衡;交换达到均衡也不能保证生产同时达到均衡。要使交换和生产同时达到均衡必须具备的条件:任意两种商品的边际替代率必须等于它们的边际转换率。
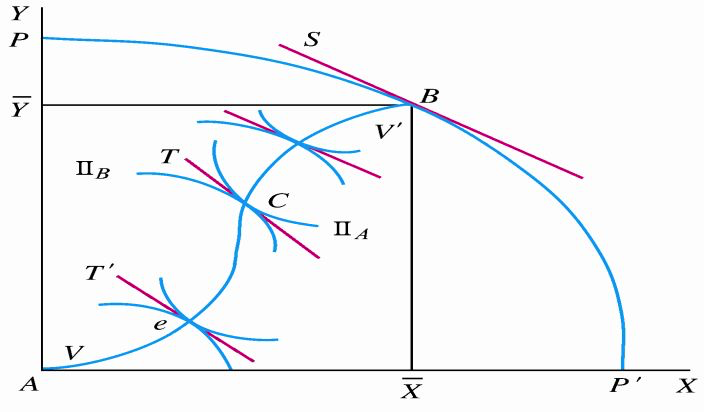
因此,"生产与交换的帕累托最优条件"为:\(MRS_{XY}=MRS_{XY}^A = MRS_{XY}^B\) ,此时达到了生产与交换的一般均衡。
原因:只有符合这一条件,才能使生产满足消费者的需要,又使资源达到有效配置。
四、完全竞争和帕累托最优状态
(一)交换的最优条件
从交换的最优条件来看,在完全竞争市场条件下,单个消费者都是价格的接受者,每个消费者都会调整对商品的需求以满足 \(MRS_{XY} =\frac {P_X } {P_Y}\),从而实现效用最大化。既然各消费者都是价格的接受者,那么各消费者购买任意两种商品的数量必使其边际替代率等于全体消费者所面对的共同的价格比率。因此,任何两种商品的边际替代率对所有的消费者都相等。
(二)生产的最优条件
从生产的最优条件来看,在完全竞争市场条件下,单个生产者都是要素价格的接受者,每个生产者都会调整要素的需求以满足 \(MRTS_{LK} = \frac {P_L} {P_K}\),从而实现利润最大化。既然各生产者都是要素价格的接受者,那么各生产者购买并使用的任意两种要素的数量必使其边际技术替代率等于全体生产者所面对的共同的要素价格比。因此,任何两种要素的边际技术替代率对所有生产者都相等。
(三)生产和交换的最优条件
ƒ从生产和交换的最优条件来看,任何两种产品生产的边际转换率即为两种商品的边际成本之比,每一消费者对任何两种商品的边际替代率等于其价格比。在完全竞争条件下,任何产品的价格等于边际成本,因此,任何两种产品的边际替代率等于它们的边际转换率。
五、社会福利函数
(一)效用可能性曲线
双方的无差异曲线的切点代表所能得到的最高效用水平。如果把这些点在横轴表示消费者 A 的效用水平,纵轴表示消费者 B 的效用水平的坐标系中表现出来,就可以得到下图中的效用可能性曲线。
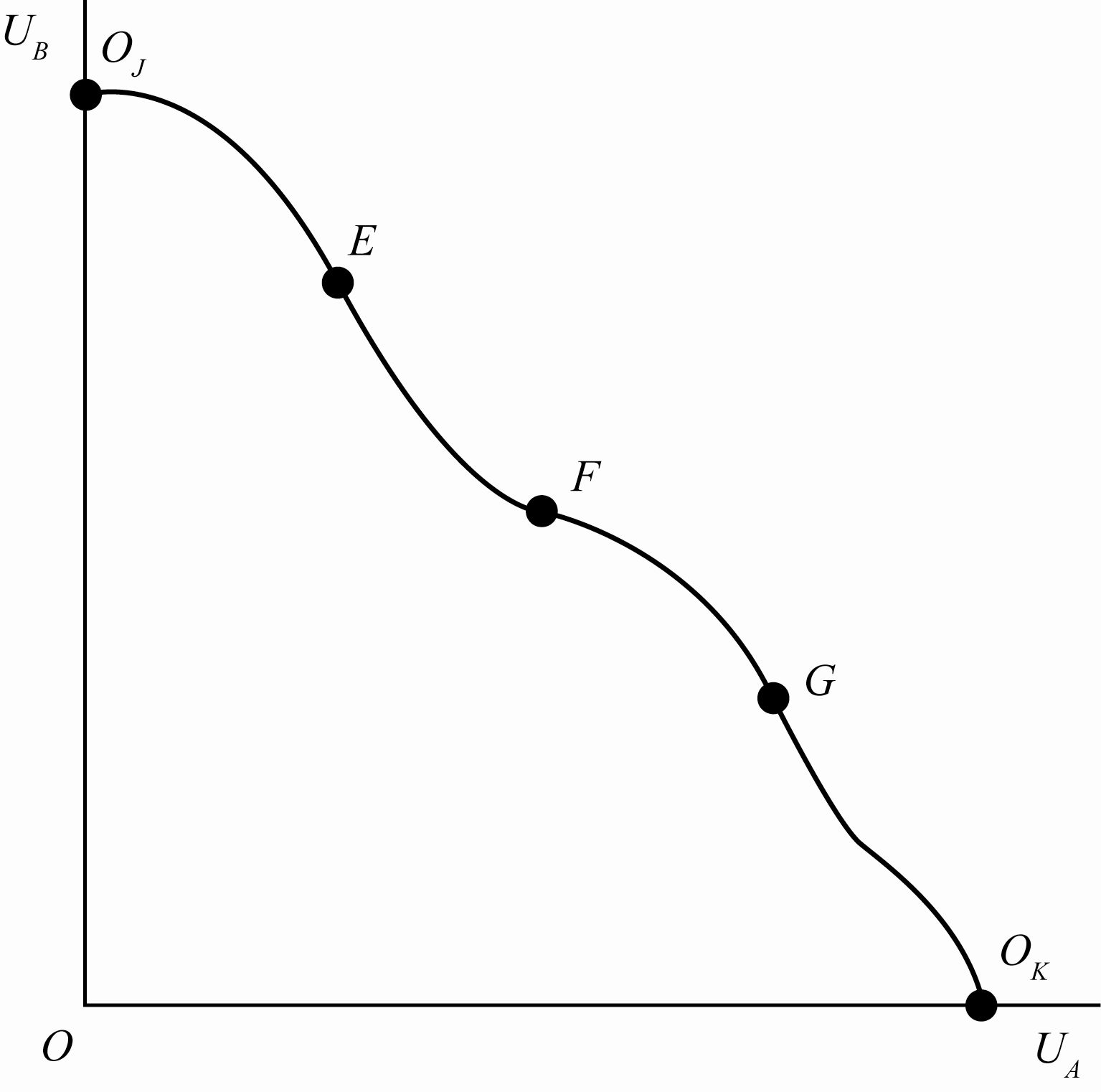
由于在最优效用水平组合中,两个消费者的效用水平反方向变化,故对应的效用可能性曲线向右下方倾斜。但是,由于效用水平的高低本来就是一个序数概念,效用可能性曲线的位置及凹凸性等无法得知。
(二)社会福利函数
假定存在某种社会福利函数(social welfare function), 该社会福利函数是个人效用函数的函数,即:
\[ \begin {align} W=W \big(U_1,U_2,\dots,U_n \big) \end {align} \]
该社会福利函数是个人效用函数的增函数,即满足:
\[ \begin {align} \frac {\partial W} {\partial U_i }\gt 0 \end {align} \]
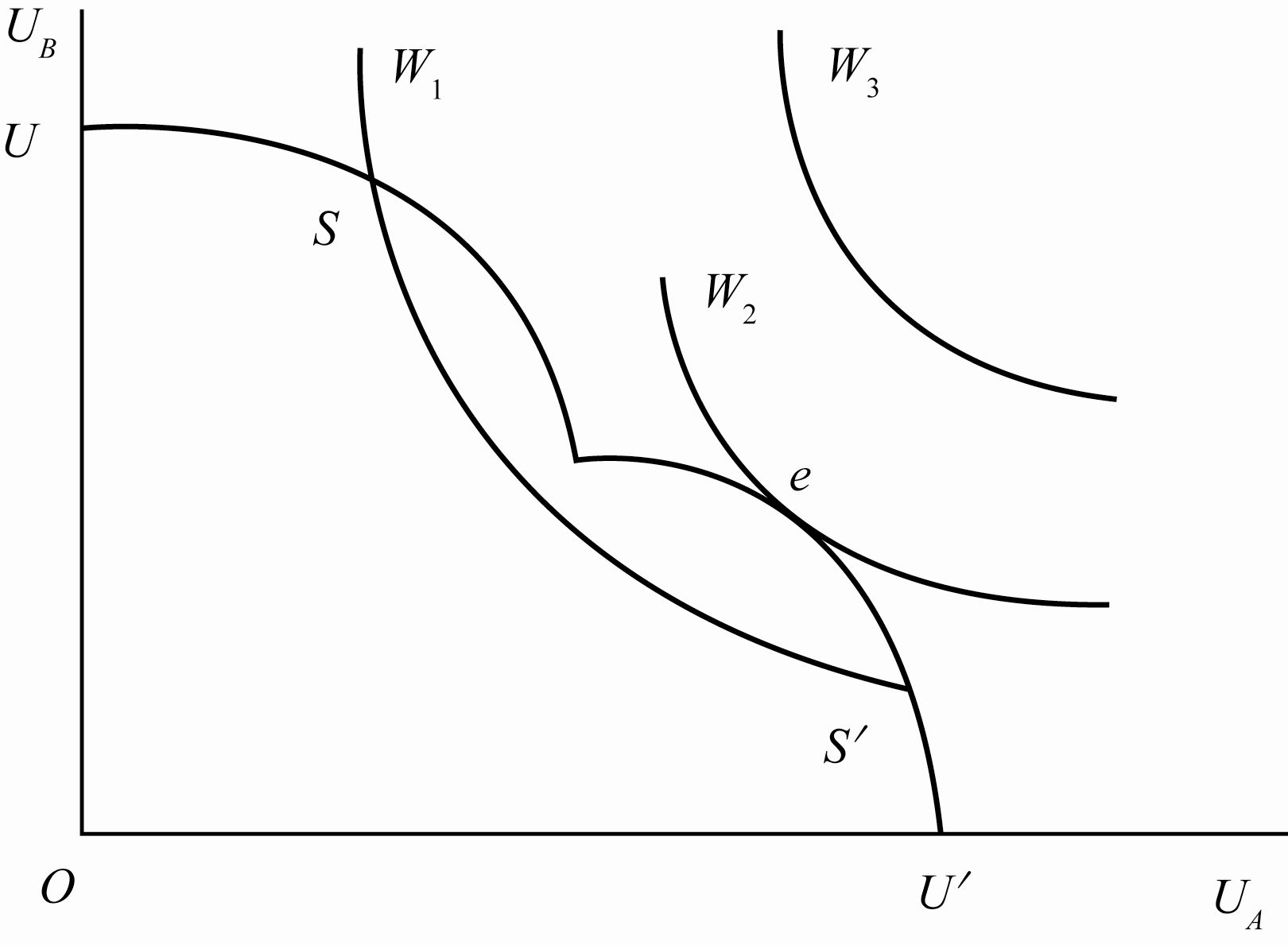
如图所示,有三条社会无差异曲线:\(W_1\)、\(W_2\)、\(W_3\),这种曲线不计算社会福利的大小,但能比较社会福利的高低,位置越高的社会无差异曲线代表的社会福利越大。 \(UU'\) 是总效用可能曲线,它类似于消费者行为理论中的收入约束线。同样的道理,最大的社会福利只会出现在总效用可能线 \(UU'\) 和社会无差异线 \(W_2\) 的切点上,这一点称为“限制社会下的最大满足点”。这是能导致最大社会福利的生产、交换和分配的唯一一点。
按照这种分析方法,只要给定个人效用函数,在个人效用函数基础之上的社会福利函数以及转换函数,通过求个人效用最大化可以导出帕累托最优状态。由此可见,彻底解决资源配置问题的关键在于社会福利函数。
(三)阿罗不可能定理
社会福利函数的形成,就是在已知社会所有成员的个人偏好次序的情况下通过一定的程序,把各种各样的个人偏好次序归结为单一的社会偏好次序。偏好的“加总”是指在所有经济行为人的偏好给定的情况下,通过一定的方法用这些信息来描述社会对各种配置的偏好顺序即社会偏好。显然,这种排列还依赖于将众多消费者的偏好进行“加总”的方法。多数人投票的方法得到的社会偏好并不是形状良好的,因为这些偏好具有不传递性。
| 行为人 1 | 行为人 2 | 行为人 3 |
|---|---|---|
| \(x\) | \(y\) | \(z\) |
| \(y\) | \(x\) | \(x\) |
| \(z\) | \(z\) | \(y\) |
如上表所示,改变投票表决顺序,将得出完全不同的选择结果,即可以通 过改变投票表决顺序来操纵投票结果。
阿罗不可能定理:用投票的方式不可能把个人的偏好集中起来,形成合乎理性的社会偏好。即在非独裁(即社会偏好不能以一个人或少数人的偏好决定)的情况下,不可能存在有适用于所有个人偏好类型的社会福利函数。
(四)不同的社会福利函数与均衡的多样性
不同的经济学家从不同的角度,采用不同的社会福利函数,从而得出对社会福利的不同观点。
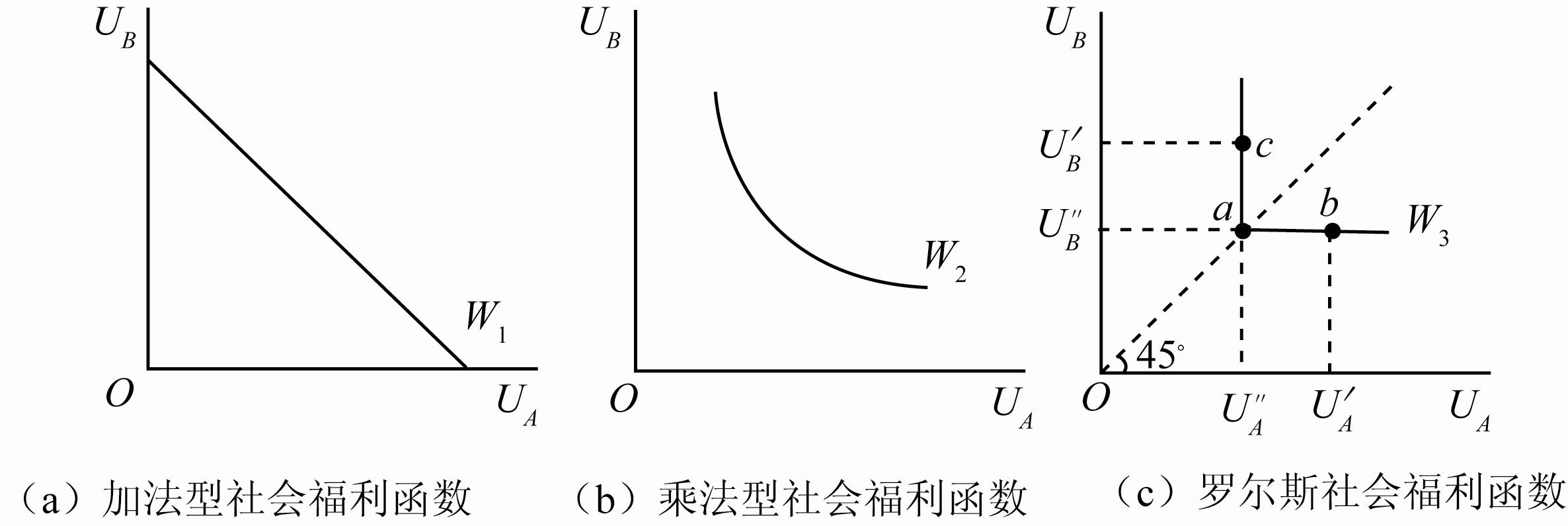
1. 加法型社会福利函数(功利主义社会福利函数)
如果一个社会强调的是所有成员的效用总和(而非其分配),则它的社会福利函数就可以写成如下的加法形式:
\[ \begin {align} W(x)= U_A(x)+U_B(x) \end {align} \]
功利主义社会福利函数赋予每个人的效用同样的权数,并随之将社会所有成员的总效用最大化。
加法型社会福利函数或直线型社会无差异曲线意味着,社会福利的大小只取决于社会成员的效用总和,而与其分配无关。换句话说,无论是穷人还是富人,其效用的增加对社会福利的贡献都是一样的。
2. 乘法型社会福利函数
如果一个社会比功利主义更加重视收入的分配和平等问题,则它的社会福利函数就可能具有如下的乘法形式:
\[ \begin {align} W(x)= U_A(x) \cdot U_B(x) \end {align} \]
乘法型社会福利函数或双曲线型社会无差异曲线意味着,当社会成员的效用总量给定时,分配越是平等,社会福利就越大,反之,分配越不平等,社会福利就越小。
3. 罗尔斯社会福利函数
罗尔斯社会福利函数更加重视提高社会上状况最差的那些人的生活水平。它可以写成:
\[ \begin {align} W(x)=\min \left \{ U_A(x), U_B(x) \right \} \end {align} \]
4. 社会公平
从最平均到最不平均:

六、效率与公平
(一)效率与公平的矛盾
缺乏公平的效率提高;缺乏效率的公平增进。
(二)“效率优先”和“兼顾公平”
所谓效率优先就是在决定收入分配的问题上,首先考虑效率,把效率当作决定收入分配的第一位因素。经济效率高,所得到的收入也高;反之情况相反。只有在保证效率的基础上,再考虑兼顾公平的问题。
兼顾公平不是必须要平等。可以从以下几个方面做到效率优先、兼顾公平:
- 减少和消除不合理的收入;
- 促进机会均等;
- 限制某些行业、某些个人的垄断性收入;
- 实现生存权利和消灭贫穷。
相关资源:

