宏观｜第2章：国民收入的决定：收入—支出模型

【内容速查与目录】

【笔记下载】

---

　　现代宏观经济学的奠基人凯恩斯的学说的中心内容是国民收入决定理论。凯恩斯主义的全部理论涉及四个市场：产品市场､货币市场､劳动市场和国际市场。仅包括产品市场的国民收入决定理论称为简单的国民收入决定理论，即收入—支出模型。

一、均衡产出

　　社会产出水平究竟由社会总需求还是由社会总供给能力决定，这实际上是从凯恩斯开始的现代宏观经济学与凯恩斯以前的古典和新古典传统经济学的分水岭。在 20 世纪 30 年代经济大萧条的背景下（编者注：建议读者结合大萧条的背景来理解凯恩斯学说的理论体系），凯恩斯在名著《就业、利息和货币通论》一书中提出了生产和收入取决于总需求的理论。

（一）短期分析假设前提

1. 经济中存在着生产能力的闲置

　　生产能力的闲置包括两层含义：

• 劳动力资源没有得到充分利用，即存在着失业；
• 厂房、机器等资本品没有得到充分利用，即存在着开工率不足。

2. 价格水平固定不变

　　凯恩斯认为，在短期内，价格机制是一种僵化的、不易变动的机制，即存在价格刚性。

　　价格刚性表现为两个方面：

• 在劳动力市场，即使存在失业，工资也不会下降；
• 在产品市场，即使存在生产过剩，物价也不会下降。

3. 在既定的价格水平上，总供给是无限的

　　在既定的价格水平上，总供给是无限的。反映在图表上，体现为总供给曲线平行于横轴（如下图 \(AE\) 曲线）。

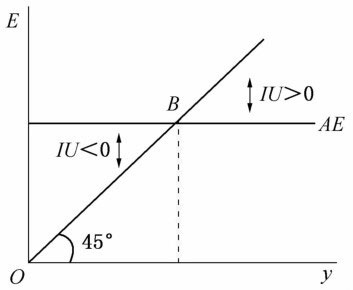
　　经济含义：由于存在资源闲置，在固定的价格水平下，要什么有什么，要多少有多少。

4. 均衡的国民收入由总需求单方面决定

　　由于总供给无限，所以均衡的国民收入由总需求单方面决定（总需求分析）。

　　在短期中，国民收入决定于总需求，这是凯恩斯经济学的一个基本原理。产量由总需求决定，是就非充分就业状态而言的，而非充分就业是一种通常的状态。

（二）均衡产出与非计划存货投资

1. 模型假设

• 二部门经济：不存在政府，也不存在对外贸易，经济中只有居民户和厂商，总需求由居民消费和企业投资构成，只企业投资是自发的或外生的，不随利率和产量而变动。
• 凯恩斯定律：假设不论需求量为多少，经济社会均能以不变的价格提供相应的供给量。
• 折旧和公司未分配利润为零。

2. 均衡产出的概念

　　均衡产出是和总需求相等的产出，即经济社会的总产出或总收入正好等于全体居民和企业想要有的支出。

　　由于两部门经济假设，均衡产出可以表示为：\(Y=C+I\)

　　其中，\(C\) 与 \(I\) 分别代表计划消费、计划投资，而不是国民收入构成公式中实际发生的消费和投资。

　　经济社会的收入正好等于全体居民和企业想要有的支出时，经济社会达到均衡。在这个模型中，存货在调整过程中起着重要的作用。从上图可以看出，非计划存货投资是一种产量调节机制，而不是古典学派强调的价格调节机制。

3. 投资等于储蓄

　　均衡产出或收入的条件也可用 \(I=S\) 表示。

　　推导：

　　计划支出等于计划消费家投资，即 \(E=C+I\)；

　　收入等于计划消费加计划储蓄，即 \(Y=C+S\)；

　　而 \(E=Y\)，于是可得投资等于储蓄，即 \(I=S\)。

　　注意：

• 国民收入核算中的 \(I=S\) 是指实际发生的投资（包括计划投资和非计划存货投资）始终等于储蓄。
• 这里的投资等于储蓄，是指经济要达到均衡，计划投资必须等于计划储蓄；而投资—储蓄恒等式中的投资恒等于储蓄，指的实际投资和实际储蓄是根据定义而得到的实际数字，从而必然相等。

二、凯恩斯的消费理论

（一）消费函数

1. 消费函数

　　在宏观经济学中，价格水平不变，所以消费数量只是收入水平的函数。消费函数是消费支出与个人可支配收入之间的依存关系。凯恩斯认为：随着收入的增加，消费也会增加，但是消费的增加不及收入增加的多，消费和收入的这种关系称做消费函数或消费倾向，用公式表示是：\(C=C(Y)\)。

　　若消费与收入之间存在线性关系，则可表示为：

\[ \begin {align} C=α+βY \end{align} \]

　　其中，\(α\) 为必不可少的自发消费部分，即收入为 0 时举债或动用过去的储蓄也必须要有的基本生活消费；\(β\) 为边际消费倾向，\(βY\) 的乘积表示收入引致的消费。

　　因此，\(C=α+βY\) 的经济含义是：消费等于自发消费与引致消费之和。当消费和收入之间呈线性关系时，消费函数就是一条向右上方倾斜的直线，消费函数上每一点的斜率都相等，并且大于 0 而小于 1。

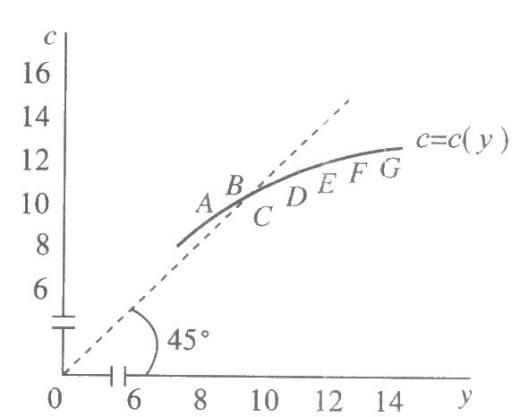
2. 边际消费倾向

　　边际消费倾向（MPC）指增加的消费与增加的收入之比率，也就是增加的 1 单位收入中用于增加消费部分的比率，边际消费倾向的公式是：

\[ \begin {align} MPC=\frac {\Delta C} {\Delta Y} =\frac {dC} {dY} \end{align} \]

　　MPC 是消费曲线上任一点切线的斜率，不论 MPC 是常量还是变量，它总是一个小于 1 的正数，即 \(0＜MPC＜1\)。

　　当消费函数为线性函数时， \(MPC=\beta\)。

3. 平均消费倾向

3.1 概念

　　平均消费倾向（APC）指任一收入水平上消费支出在收入中所占的比率。平均消费倾向的公式是：

\[ \begin {align} APC=\frac {C} {Y} \end{align} \]

3.2 取值

　　APC 是消费曲线上任一点与原点相连而成的射线的斜率。

• 若 \(APC＜1\)，此时消费总量 ＜ 收入总量（产生储蓄）;
• 若 \(APC=1\)，此时全部收入都用于消费（储蓄为零）;
• 若 \(APC＞1\)，此时消费总量大于收入总量（负债消费，即产生负储蓄）。

3.3 APC 与 MPC 的关系

　　当消费函数为线性函数时：

\[ \begin {align} APC=\frac \alpha Y+\beta \end{align} \]

　　即平均消费倾向总是大于边际消费倾向。

（二）储蓄函数

1. 储蓄函数

　　储蓄函数是描述储蓄随收入变化而变化的函数，其公式是：

\[ \begin {align} S=S(Y) \end{align} \]

　　当消费函数为线性函数时：

\[ S=Y-C=Y-(\alpha +\beta Y)=-\alpha+(1-\beta)Y \]

2. 边际储蓄倾向

　　边际储蓄倾向（MPS）是该点上的储蓄增量对收入增量的比率，其公式是：

\[ \begin {align} MPS=\frac {\Delta S} {\Delta Y} =\frac {dS} {dY} \end{align} \]

　　边际储蓄倾向为储蓄曲线上任一点的斜率。

　　当储蓄函数为线性函数时，\(MPS= 1-\beta\)。

3. 平均储蓄倾向

　　平均储蓄倾向（APS）是指任一收入水平上储蓄在收入中所占的比率，其公式是：

\[ \begin {align} APS=\frac S Y \end{align} \]

　　平均储蓄倾向是储蓄曲线上任一点与原点相连而成射线的斜率。

　　当储蓄函数为线性函数时：

\[ \begin{align} APS=- \frac {\alpha} {Y}+(1-\beta) \end{align} \]

（三）消费函数和储蓄函数的关系

　　由于储蓄被定义为收入和消费之差，因此：

• 消费函数和储蓄函数互为补数，二者之和总等于收入，即：\(C+S=Y\)；
• \(APC\) 和 \(MPC\) 都随收入增加而递减，且 \(APC＞MPC\)；
• \(APS\) 和 \(MPS\) 都随收入增加而递增，且 \(APS＜MPS\)；
• \(APC+APS \equiv1\)，\(MPC+MPS \equiv1\)。

　　消费和储蓄的关系如下图所示：

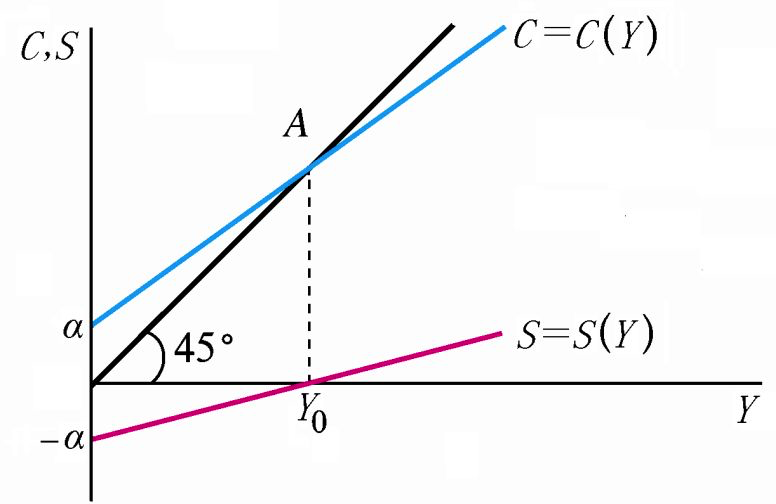
• 在 A 点左边，消费大于收入，为负储蓄；
• 在 A 点右边，消费小于收入，为正储蓄；
• 在 A 点，消费等于收入，储蓄为0。

（四）家户消费函数和社会消费函数

　　社会消费函数并不是家户消费函数的简单加总。从家户消费函数求取社会消费函数时，还要考虑以下一系列限制条件：

• 国民收入的分配：富者边际消费倾向较低，穷者边际消费倾向较高。国民收入分配越不均等，社会消费曲线就越是向下移动。
• 政府税收政策：若实行累进个人所得税，将富有者的收入转移给穷人用于消费，则社会消费数量增加，社会消费曲线向上移动。
• 公司未分配利润在利润中所占比例：所占比例越大，消费越少，社会消费曲线下移；反之，社会消费曲线上移。

（五）影响消费的其他因素

• 利率
• 价格水平
• 收入分配
• 社会保障制度

三、国民收入的决定

（一）两部门经济

1. 使用消费函数决定收入

　　在两部门经济中，不存在政府部门，也不存在国外部门。由于不存在政府部门，因此可支配收入 \(Y_D=Y\)。

　　假定：

• 只有家庭部门与企业部门；
• 投资是外生变量，投资不变。

　　总支出 \(AE=C+I_0= \alpha + \beta Y + I_0\)，结合产品市场均衡条件 \(AE=Y\)，可得：

\[ \begin {align} Y= \alpha + \beta Y + I_0 \end{align} \]

　　由上式可以解得均衡产出水平为：

\[ \begin {align} Y_0= \frac 1 {1-\beta}(\alpha + I_0) \end{align} \]

2. 使用储蓄函数决定收入

\[ \left \{ \begin {align} & I_0=S=Y-C \notag \\ & S=-\alpha+(1-\beta)Y \notag \end {align} \right. \]

　　由上式可以解得均衡产出水平为：

\[ \begin {align} Y_0= \frac 1 {1-\beta}(\alpha + I_0) \end{align} \]

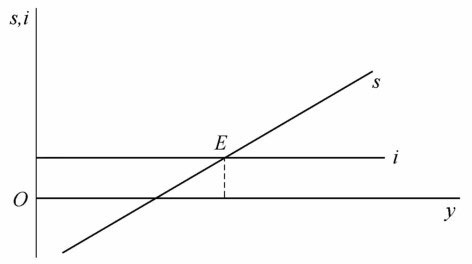
　　用计划投资等于计划储蓄的方法决定收入，也可以用下图表示：

　　‍

（二）三部门经济

　　三部门经济，即在两部门经济的基础上加入政府部门，需考虑政府购买、税收和转移支付等政府行为因素。政府的收入主要来自税收，税收包括两种：一种是定量税，税收量不随收入而变动；另一种是比例所得税，税收量随收入的增加而增加。政府购买与转移支付一般为某一确定的值，是个外生变量。

1. 征收定量税

　　假定投资为 \(I_0\)，政府支出为 \(G_0\) ， 税收为 \(T_0\) ， 转移支付为 \(T_r\)。消费取决于可支配收入，则有：

\[ \left \{ \begin {align} & Y_D=Y- T_0 + T_r \notag \\ & C=\alpha +\beta Y_D \notag \\ & AE=C+ I_0 + G_0 \notag \\ & AE=Y \notag \\ \end {align} \right. \]

　　由上式可以解得均衡产出水平为：

\[ \begin {align} Y_0= \frac 1 {1-\beta} \Big[\alpha -\beta ( T_0 - T_r)+ I_0 + G_0 \Big] \end{align} \]

2. 征收比例税

　　假定投资为 \(I_0\)，政府支出为 \(G_0\) ， 同时征收固定税 \(T_0\) 与比利税（税率为 \(t\)），转移支付为 \(T_r\)。消费取决于可支配收入，则有：

\[ \left \{ \begin {align} & Y_D=Y- T + T_r \notag \\ & C=\alpha +\beta Y_D \notag \\ & T=T_0 + tY \notag \\ & AE=C+ I_0 + G_0 \notag \\ & AE=Y \notag \\ \end {align} \right. \]

　　由上式可以解得均衡产出水平为：

\[ \begin {align} Y_0= \frac 1 {1-\beta(1-t)} \Big[\alpha -\beta ( T_0 - T_r)+ I_0 + G_0 \Big] \end{align} \]

　　其中：令 \(k= \frac 1 {1-\beta(1-t)} >1\)，且 \(0<t, \ \beta <1\)。\(k\) 则为封闭经济乘数。

（三）四部门经济

1. 推导与求解

　　四部门经济即在三部门的基础上加入净出口一项。其中，进口函数是收入的线性函数，不是可支配收入的函数，因为包括政府的进口。出口是由外国的购买力和购买愿望决定的，本国一般难以影响。所以，出口一般假定为一个外生变量。

\[ \begin {align} NX=X_0-(m_0+\gamma Y) \end {align} \]

　　其中，\(X_0\) 表示出口量，为外生变量；\(m_0\) 为自发进口；\(\gamma\) 为边际进口倾向，且 \(0<\gamma <1\)。

　　假定在征收比例税三部门经济的基础上，加入对外贸易部门，则可以列出下面方程：

\[ \left \{ \begin {align} & NX=X_0-(m_0+\gamma Y) \notag \\ & Y_D=Y- T + T_r \notag \\ & C=\alpha +\beta Y_D \notag \\ & T=T_0 + tY \notag \\ & AE=C+ I_0 + G_0 +NX \notag \\ & AE=Y \notag \\ \end {align} \right. \]

　　由上式可以解得均衡产出水平为：

\[ \begin {align} Y_0= \frac 1 {(1+\gamma )-\beta(1-t)} \Big[\alpha -\beta ( T_0 - T_r)+ I_0 + G_0 + X_0-m_o\Big] \end{align} \]

　　其中：令 \(k=\frac 1 {(1+\gamma)-\beta(1-t)}\)，则 \(k\) 为开放经济乘数，也称作对外贸易乘数。

2. 封闭经济乘数与开放经济乘数的比较

　　由三部门经济均衡产出可得，在征收比例税的前提下，封闭经济乘数为：

\[ \begin {align} k= \frac 1 {1-\beta(1-t)} \end {align} \]

　　由四部门经济均衡产出可得，在征收比例税的前提下，开放经济乘数为：

\[ \begin {align} k=\frac 1 {(1+\gamma)-\beta(1-t)} \end {align} \]

　　比较两个乘数：

\[ \begin {align} \frac 1 {1-\beta(1-t)} \gt \frac 1 {(1+\gamma)-\beta(1-t)} \end {align} \]

　　即：\(封闭经济乘数\gt开放经济乘数\)，这是因为增加的收入的一部分被用于购买进口商品。

四、乘数论

　　乘数（Multiplier）是宏观经济学的一个术语，是指每单位外生变量的变化所带来的引致变量的变化情况。其原因是，各经济部门是相互关联的，某一部门的一笔投资（或收入变动）不仅会影响本部门的收入，而且会在国民经济其他部门中引起连锁反应，从而影响这些部门的投资与收入。

（一）乘数理论

1. 推导

　　假设增加自主支出 \(\Delta {\overline A}\)，则产出（或者总支出）的增加量为：

\[ \begin {align} \Delta AE=(1+β+β^2+…+β^{n-1}) \Delta {\overline A} =\frac 1 {1-\beta} \Delta {\overline A} \equiv \Delta Y_0 \end {align} \]

　　其中，倍数 \(\frac 1 {1-\beta}\) 称为乘数（multiplier），即自主性总支出增加 1 单位时，均衡产出的变动量。可以看出，边际消费倾向越大，乘数也越大。

2. 图解

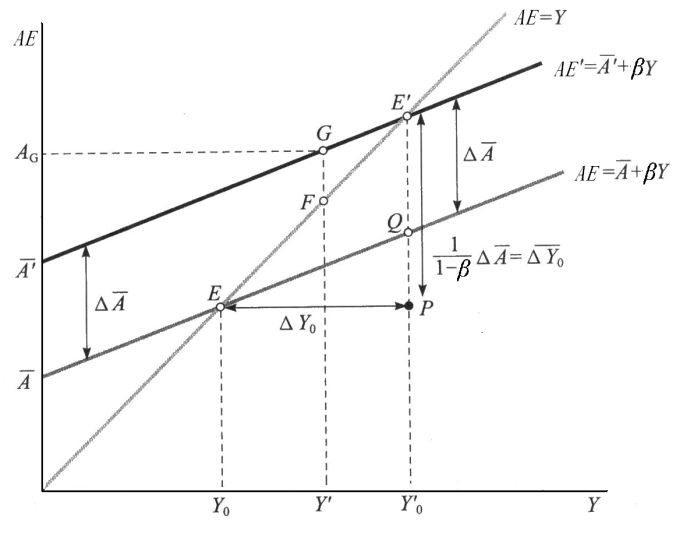
　　如上图所示，起始的均衡点为 \(E\)，对应的均衡收入水平 \(Y_ 0\)。自主支出从 \(\overline A\) 增加到 \(\overline {A'}\)，使得总支出曲线 \(AE\) 平行向上移位到 \(AE'\)，达到新的均衡点 \(E'\)，对应的均衡收入水平 \(Y'_0\)。显然，\(\Delta {\overline A} < \Delta Y_0\)。

（二）两部门经济

　　投资乘数/凯恩斯乘数：收入的变化与带来这种变化的投资支出的变化的比率。

　　原理：\(I\uparrow \Longrightarrow AE \uparrow \Longrightarrow Y\uparrow (AE=Y)\)

　　由上可知，两部门经济的均衡产出为：\(Y_0= \frac 1 {1-\beta}(\alpha + I_0)\)，因此投资乘数为：\(k_I=\frac 1 {1-\beta}\)。自发支出 \(α\) 的乘数同样也是 \(k_{\alpha}=\frac 1 {1-\beta}\)。

推导补充：

方法一：数学推导

新增投资 \(\Delta I\) 对经济的拉动作用包括以下几个步骤：

第一轮：增加的投资 \(ΔI\) 使得国民收入 \(Y\) 第一轮直接增加 \(ΔI\)

第二轮：第一轮拉动的国民收入 \(Y\)，会在第二轮拉动消费增长 \(\beta \Delta I\)

第三轮：第二轮消费拉动的国民收入增加 \(\beta \Delta I\)，会在第三轮拉动消费增长 \({\beta}^2 \Delta I\)

......

第 n 轮：第 n-1 期拉动的国民收入增加 \({\beta}^{n-2} \Delta I\)，会在第 n 轮拉动消费增长 \({\beta}^{n-1} \Delta I\)

当 \(n \to \infty\) 时，新增投资 \(\Delta I\) 会使得国民经济增长 \(ΔY=ΔI(1+β+β^2+…+β^{n-1}) = \frac 1 {1-\beta} \Delta I\)，即投资乘数为 \(k_I=\frac {\Delta Y} {\Delta I}=\frac 1 {1-\beta}\)

上面计算过程使用了无穷级数求和公式，\(0<\beta<1\)，\(\sum_{n=0}^{\infty} { \beta^{n} }=\frac 1 {1-\beta}\)。

方法二：均衡分析

均衡时收入=支出，那么当投资变化时，从一个均衡转化为另一个均衡，必然存在收入的变化量 \(ΔY\) 等于支出变化量。如果把支出变化量分解成投资引起的直接需求 \(ΔI\) 和收入变化带来的消费变化 \(βΔY\)，则有 \(ΔY=ΔI+βΔY\)，从而推出 \(\frac {\Delta Y} {\Delta I}=\frac 1 {1-\beta}=k_I\)。

方法三：微分

根据消费函数决定的国民收入公式 \(Y= \frac {\alpha + I} {1-\beta}\)，当增加 \(ΔI\) 时，\(Y'= \frac {\alpha + I+ \Delta I} {1-\beta}\)，则 \(\Delta Y=Y'-Y= \frac { \Delta I} {1-\beta}\)，即 \(\frac {\Delta Y} {\Delta I}=\frac 1 {1-\beta}=k_I\)。另外，也可以直接求微分 \(k_I=\frac {\Delta Y} {\Delta I}=\frac 1 {1-\beta}\)。

（三）三部门经济

1. 征收定量税

　　在三部门经济中，征收定量税时的均衡产出水平是：

\[ \begin {align} Y_0= \frac 1 {1-\beta} \Big[\alpha -\beta ( T_0 - T_r)+ I_0 + G_0 \Big] \end{align} \]

　　政府购买支出乘数：收入变动对引起这种变动的政府购买支出变动的比率，可表示为：\(k_g=\frac 1{1-\beta}\)

　　税收乘数：收入变动对引起这种变动的税收变动的比率，可表示为：\(k_t=\frac {- \beta}{1-\beta}\)，负号表示增税将导致国民收入下降。

　　\(T_0\downarrow \Longrightarrow Y_D \uparrow \Longrightarrow C \uparrow \Longrightarrow AE \uparrow \Longrightarrow Y \uparrow (AE=Y)\)

　　政府转移支付乘数：收入变动对引起这种变动的政府转移支付变动的比率，可表示为：\(k_{t_r}=\frac { \beta}{1-\beta}\)。

补充：

从绝对值来看，\(\left| k_t \right| = \left| k_{t_r} \right| < \left| k_g \right|\)

原因：政府购买直接增加了总支出，而减税或者政府转移支付只会使可支配收入增加相应的数额，增加的可支配收入只有一部分用于消费支出。正是因为政府购买支出乘数大于税收乘数，因此，如果政府购买支出和税收等额增加，国民收入仍将增加。

　　平衡预算乘数：政府收入和支出同时以相等数量增加或减少时，国民收入变动与政府收支变动的比率，即：\(k_b=1\)

　　平衡预算乘数推导：因为 \(ΔG=ΔT\)，由上式可得，\(\Delta Y=\frac 1{1-\beta}ΔG+\frac {- \beta}{1-\beta}ΔT=\Delta Y\)，因此 \(k_b=k_g+k_t=1\)

2. 征收比例税

　　在三部门经济中，如果征收比例税，均衡产出水平为：

\[ \begin {align} Y_0= \frac 1 {1-\beta(1-t)} \Big[\alpha -\beta ( T_0 - T_r)+ I_0 + G_0 \Big] \end{align} \]

　　此时：

　　政府购买支出乘数：\(k_g=\frac 1{1-\beta(1-t)}\)

　　税收乘数：\(k_t=\frac {- \beta(1-t)}{1-\beta(1-t)}\)

　　政府转移支付乘数：\(k_{t_r}=\frac {\beta (1-t)}{1-\beta(1-t)}\)

　　平衡预算乘数：\(k_b=k_g+k_t=1\) 仍然成立。

　　即不论是征收定量税还是比例税，平衡预算乘数均为 \(k_b=1\)。

数学补充：

税收与政府转移支付会直接影响居民的可支配收入，税收会降低可支配收入，政府转移支付则会提高可支配收入，两者的乘数相同，但符号相反。

推导过程：以征收比例税 \(\Delta T= t \cdot Y\) 为例：

第一轮：可支配收入变为\(Y_D=(1-t)Y_0\)，因此消费变化\(\Delta C_1=-\beta (1-t) \Delta T\)，消费的降低直接导致均衡产出减少\(\Delta Y_1=\Delta C_1\)；

第二轮：第一轮均衡产出下降导致可支配收入下降，此时消费变化\(\Delta C_2=-\beta^2 (1-t)^2 \Delta T\)，导致均衡产出下降\(\Delta Y_2=\Delta C_2\)；

......

第 n 轮：第 n-1 轮均衡产出下降导致可支配收入下降，此时消费变化\(\Delta C_n=-\beta^n (1-t)^n \Delta T\)，导致均衡产出下降\(\Delta Y_n=\Delta C_n\)。

当 \(n \to \infty\) 时，征收比例税 \(\Delta T=tY\) 会使得均衡产出变化：

\[ \begin{align} \Delta Y & = \sum^{\infty}_{n=1} {\Delta Y_n} = \sum^{\infty}_{n=1} {\Delta C_n} \notag \\ & = \sum^{\infty}_{n=1} \Big[-\beta^n (1-t)^n \Delta T \Big] \notag \\ & = - \beta (1-t) \cdot \sum^{\infty}_{n=0} \Big[-\beta^n (1-t)^n \Delta T \Big] \notag \\ & = \frac {-\beta (1-t)} {1-\beta(1-t)} \Delta T \end{align} \]

因此，税收乘数为：\(k_t=\frac {- \beta(1-t)}{1-\beta(1-t)}\)。

这里使用了无穷级数求和公式来进行计算。\(0<\beta<1\)，\(\sum_{n=0}^{\infty} { \beta^{n} }=\frac 1 {1-\beta}\)。

注意：征收比例税情况下的税收乘数要区别于自发性税收乘数（总税收中的定量税部分），自发性税收乘数为\(k_{t_0} = \frac {- \beta} {1-\beta}\)，与三部门经济中征收定量税的税收乘数相同。

参考资料：比例税制下的税收乘数及平衡预算乘数探讨

（四）四部门经济

　　对外贸易乘数：收入变动对引起这种变动的出口变动的比率，公式为：

\[ \begin {align} k_x = \frac 1 {(1 + \gamma) -\beta(1-t) } \end {align} \]

　　注意：在四部门经济假设下，收入决定公式为：

\[ \begin {align} Y_0= \frac 1 {(1+\gamma )-\beta(1-t)} \Big[\alpha -\beta ( T_0 - T_r)+ I_0 + G_0 + X_0-m_o\Big] \end{align} \]

　　因此不仅 \(k_x = \frac 1 {(1 + \gamma) -\beta(1-t) }\)，自发支出乘数、投资乘数和政府购买支出乘数也都等于 \(\frac 1 {(1 + \gamma) -\beta(1-t) }\)。

　　因为 0 \(＜γ＜1\)，可见开放经济条件下的乘数小于封闭经济条件下的乘数，原因在于由出口导致增加的收入中的一部分用于进口。

---

相关资源：

1. 经济学笔记下载
2. 《微观经济学》内容速查与笔记目录
3. 《宏观经济学》内容速查与笔记目录