发展经济学｜附录A1-资本-劳动比率的提高和生产函数的移动

　　技术进步对经济增长贡献的变化，是增长类型变化的主要因素。在现代经济学中，技术进步被定义为生产函数的向上移动。生产函数可以写作：

\[ \begin{align} Y = F(L,K) \end{align} \]

　　其中，\(F\) 对 \(L\) 和 \(K\) 可微分，且满足：

　　前两个条件即为稻田条件。

　　假定 \(F\) 是线性齐次生产函数，具有规模报酬不变的特征。那么，劳动生产率 \(y=\frac Y K\) 可以表示为资本-劳动比率 \(k=\frac K L\) 的函数。那么，原生产函数可以写作：

\[ \begin{align} y= f(k) \end{align} \]

1. 技术水平恒定情况

　　当技术水平恒定（不存在技术进步）时，\(f\) 的图像可以表示为：

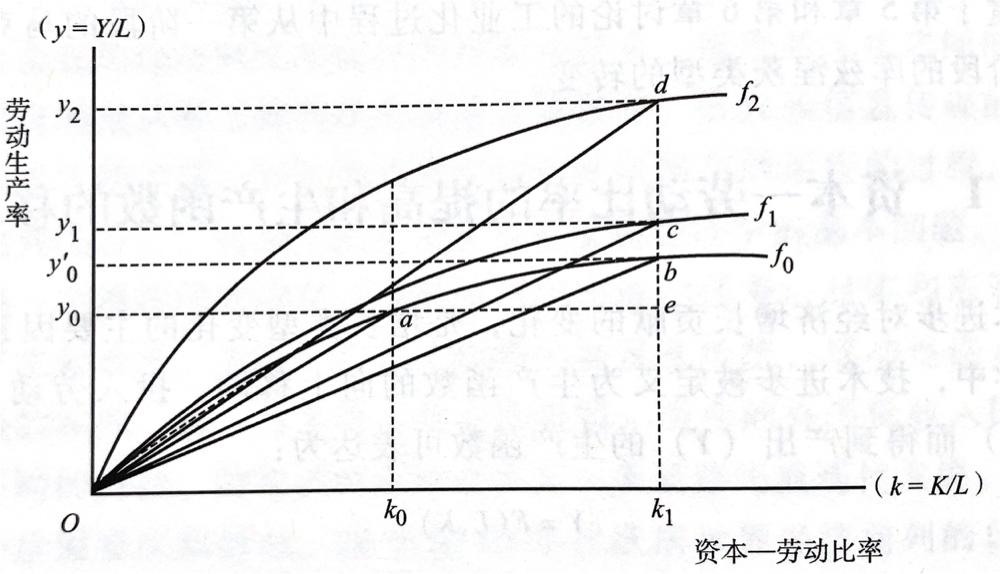
劳动生产率增长的原理

　　假定在初始期 \(t=0\)，生产函数为 \(y_0\)，资本-劳动比率为 \(k_0\)，则 \(y_0=f_0(k_0)\)。此时，资本生产率 \(Y/K\)（资本与产出水平的倒数）为直线 \(Oa\) 的斜率。

　　在 \(t=1\) 时，由于不存在技术进步，生产函数仍为 \(f_0\) 保持不变，资本-劳动比率 \(k_0 \to k_1\)，资本生产率将由直线 \(Oa\) 斜率下降至直线 \(Ob\) 斜率。

　　因此，若生产函数符合线性齐次特征且技术水平不变，单位劳动的资本使用量 \(k = \frac K L\) 提高，会导致资本产出比率 \(K/Y\) 提高。（投资效率降低）

　　经济增长，特别是人均产出的增加，大致可以分为两个阶段：

　　在第一阶段：有形资本积累

　　在 \(t : 0 \to 1\) 的第一阶段，技术也并非保持不变。

　　假定该时期内，生产函数移动 \(f_0 \to f_1\) 相对于资本-劳动比率 \(k_0 \to k_1\) 增加很小，那么：

　　因此：\(\frac {eb} {ec} \gt \frac {bc} {ec}\)，即资本增长带来的产出增加效率更高、贡献更大，虽然投资增加会导致技术进步，体现在生产函数上移 \(bc\)，但是投资增加主要促进资本增长进而促进产出增加。

　　此时，直线 \(Oc\) 的斜率小于直线 \(Oa\) 的斜率，导致资本产出比率上升（投资效率降低）。

　　在第二阶段：无形资本积累

　　在 \(t : 0 \to 2\) 的第二阶段，生产函数变动 \(f_0 \to f_2\)：

　　因此：\(\frac {eb} {ed} \lt \frac {bd} {ed}\)，即与资本增长相比，技术进步带来的生产函数上移是劳均生产率提高的主要来源。

　　此时，直线 \(Od\) 的斜率大于直线 \(Oa\) 的斜率，导致资本产出比率下降（投资效率提高）。

　　总结：

　　‍