发展经济学｜第4章：经济增长来源的探讨：资本积累与技术进步

参考内容：

速水佑次郎 《发展经济学（第 3 版）》 chap 5、chap 6

一、经济发展中的资本积累

　　即使在强烈的人口压力下，自然资源枯竭的低收入经济体，只要农村的广大小生产者能够得到适当的公共品供给，就可以实现经济发展。低收入国家在发展初期面临的主要问题是促进劳动对自然资源的替代，使劳动和资本互补性增长。在实现工业化后，低收入国家对自然资源的依赖程度会降低，持续的经济增长将转化为促进资本积累和资本对劳动的替代。

　　两个经济阶段的不同关注点：

• 自然资源禀赋制约阶段：人口爆炸式增长导致的自然资源禀赋短缺，成为制约经济发展的关键问题。应当关注通过增加资本和劳动投入，来提高自然资源的生产力。
• 产业革命阶段：人口增长率已经放缓，自然资源约束不再是经济增长面临的关键问题。在产业革命以来的新技术体制下，应当关注使用资本替代劳动，提高劳动生产率。

　　许多发展中国家在自然资源禀赋约束阶段，依靠政府命令的方式实现资本积累。这些发展中国家大规模开办工厂，并从发达国家引进劳动节约型的技术装备，而没有对引进的技术进行适应性调整，难以实现相对稀缺的资本的高效利用。在此种情况下，通过行政命令土改储蓄率高和投资率，可能会导致其在工业化进程中面临发展停滞。

　　经济增长率的决定性因素：1）有资本积累率；2）资本在各种投资机会中的配置，特别是有形资本和无形资本之间的配置。

1. 从亚当·斯密到马克思

　　自亚当·斯密以来，经济学中普遍认为资本积累是经济增长的发动机，实现高资本积累率的机制是资本主义市场经济。通过培育资本主义的市场经济体制，就可以实现经济高速增长。

1.1 亚当·斯密的资本观

　　亚当·斯密提倡自由放任和小政府，反对政府指令下的高积累模式。在自由的市场经济体制下，资本积累取决于消费份额，压制消费、高储蓄和高投资可以实现经济增长。

　　只有从事“有用的和生产行动的”工作的劳动，才为社会生产价值。资本积累对提高劳动生产率最重要，因为推动了劳动分工。

　　劳动分工促进劳动生产率提高的原因：

• 工人生产技能和熟练度提高
• 节约了在不同工作之间转换所损失的时间
• 简化和缩减劳动的机械的发明，是一个人能够做许多人的工作

　　为了实行劳动分工，企业家必须要有一定的资本存量（即工资基金），用于购买工场、生产工具和原材料，并在产品销售之前用于支付工人工资。随着企业家可利用的资本存量增加，更多不同工序上会雇佣更多的劳动力，以实现扩大劳动分工。

　　社会中的资本存量来自工业企业家的“过度节俭”积累。专制君主、有土地的贵族和有特权的商人的挥霍和渎职，会减少资本积累。减少资本的挥霍（撤销地主免税和废除商人垄断贸易许可证，削减统治体系内的俸禄），可以避免资本积累被耗竭。对工业资本家减少管制和降低税收，可以促进资本的积累。

　　（但是，资本的耗竭可能不仅仅来自以上几个来源，在统治集团和经济发展目标出现不一致时，将资本等有限的生产要素用于低效的、不能带来持续收益或不能扩大再生产的投资，可能会导致经济发展的停滞。例如：房地产、低效的基础建设工程等）

　　取消政府对生产和销售活动的干预，有利于增加企业家的收入，进而提高社会储蓄率，扩大市场容量和资本存量。

　　亚当·斯密提倡自由市场竞争，但是其观点的背景是英国重商主义政策下已经修建了大量公共基础设施（如道路、运河等），完善的公共基础设施是市场机制形成的基础。

1.2 李嘉图的修正

　　促进经济增长必须要有减少挥霍性消费、增加有用的生产性活动的投资机制。

　　在李嘉图模型中，由于受到马尔萨斯人口法则的影响，占据人口大多数的劳动者的消费被长期压制在最低生计水平上，工业产品价值中超出劳动力最低生计水平的部分被资本家获得，这保证了资本积累率和产出增长率的持续稳定，用于资本积累。

　　李嘉图认为，人口增长使得人均土地禀赋下降，食品价格上升会导致名义工资率（名义生存水平工资率）的上升，这会导致经济增长停滞。为了保持高资本积累率和高经济增长率，通过粮食进口自由化可以缓解土地资源匮乏造成的食品价格上涨。

1.3 马克思的资本主义发展模型

1.3.1 马克思理论模型简介

　　随着资本主义的扩大，被驱逐出传统职业（例如：小农和传统生产方式自我雇佣的制造业者）的人数会不断增长，会不断地产生工业后备军，剩余劳动力会一直存在。同时，资本家总是通过大规模的机械化实现资本对劳动的替代。因此，现代工业部门的就业增加要比资本积累和产出增长的速度低得多，剩余劳动力不是马尔萨斯人口法则导致的，而是资本主义的发展导致的。资本收入份额的增长是以牺牲劳动收入份额为代价的，不平等是资本主义固有的趋势。

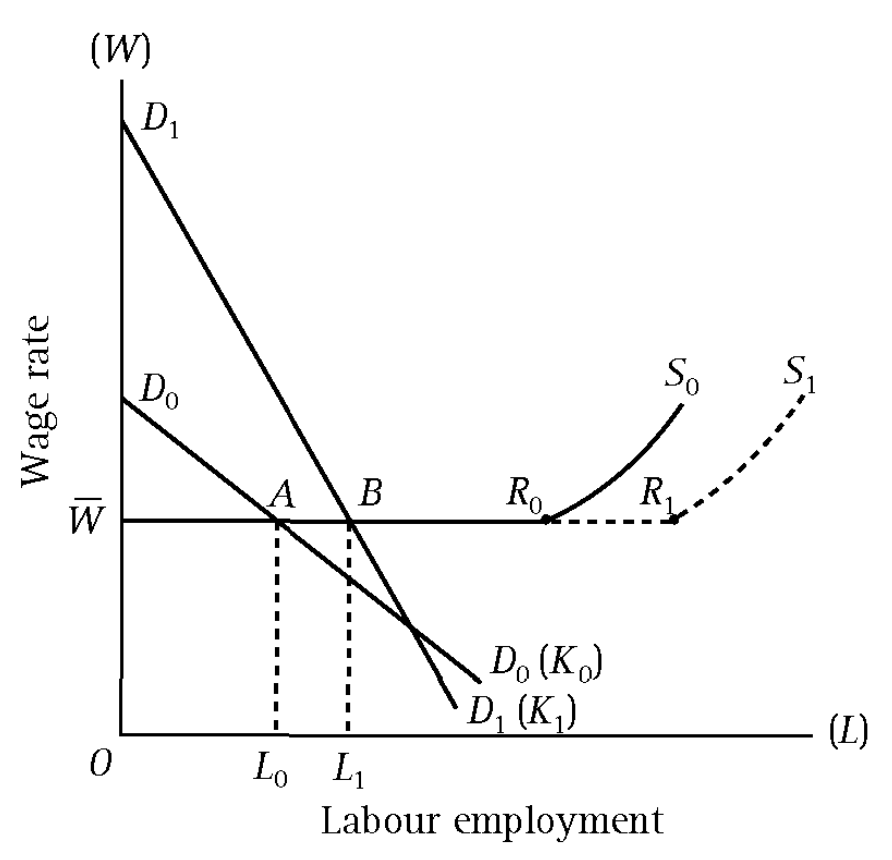
　　上图为根据现代经济学重构的马克思模型。在资本主义经济下，由于存在剩余劳动力，在生存水平工资率 \(\overline W\) 下，劳动力市场具有完全弹性（水平线 \(\overline W R_0\)）；当剩余劳动力被工业部门吸收完毕后，工资率将会上升（曲线 \(R_0 S_0\)）。

• 在初始期 \(t=0\)：资本存量为 \(K_0\)，现代资本主义部门的劳动力需求曲线为 \(D_0\)，初始均衡点为点 \(A\)，此时雇佣工人数量为 \(L_0\)，工资率为生存水平 \(\overline W\)。根据马克思的假设，在资本主义经济的工业部门，实际被雇佣的劳动力数量 \(L_0\) 远远小于劳动力总数量 \(R_0\)，\(R_0 - L_0\) 即为剩余劳动力 / 工业后备军的数量。资本家把利润 \(A D_0 \overline W\) 中的大部分用于下一期 \(t=1\) 的投资。
• 在下一期 \(t=1\)：资本存量提高 \(K_0 \to K_1\)，企业产出扩大 \(O L_0 A D_0 \to O L_1 B D_1\)，传统生产方式被资本主义生产扩张挤压，小生产者（如小农、传统自我雇佣者、家庭成员等）被迫到资本主义工业部门寻找就业机会，导致劳动供给进一步上升，体现为劳动供给曲线的水平段延长（线段 \(\overline W R_0 \to \overline W R_1\)）。

　　资本和劳动收入份额：

• 在初始期 \(t=0\)，资本收入份额为 \(A D_0 \overline W / O L_0 A D_0\)，劳动收入份额为 \(O L_0 A \overline W / O L_0 A D_0\)；
• 在下一期 \(t=1\)，资本收入份额为 \(B D_1 \overline W / O L_1 B D_1\)，劳动收入份额为 \(O L_1 B \overline W / O L_1 B D_1\)；
• 两期结果的比较：随着资本主义经济的发展，资本收入份额越来越大，劳动收入份额越来越小。

　　因此，资本主义经济不平等的增长将刺激劳动者阶级和资本家阶级之间的敌对状态，最终将导致暴力革命，并将以少数人占有资本的私有制为基础的资本主义转变为以公有制为基础的社会主义，并且社会的不稳定将会随着经济萧条的周期性发生而加剧。事实上，在发达资本主义国家中，并未发生以生产资料占有制度为特征的社会制度变革，可能原因是发达资本主义国家的矛盾转移（例如代理人战争，经济倾销，技术垄断等）、福利制度的建立和工会等劳动保障机构的建立，延缓了社会矛盾的发生。自 19 世纪末以来，西欧和北美的手机工资率一直在上升，劳动者的收入份额也在增加。

　　马克思模型对当今发展中国家的启示：将投资集中在高收入国家劳动节约型技术的现代机械和设备上，会导致就业的增长远低于产出的增长。在发展中国家，由于爆炸性的人口增长，劳动增长率很高。农业部门因土地的资源禀赋限制，对劳动力的吸纳能力达到饱和点，剩余劳动力前往城市寻求就业机会成了劳动者的理性选择。在城市的工业部门，劳动节约型技术的广泛运用不利于工业吸纳劳动力，高增长率、低就业率的问题会导致流民和城市贫民窟问题，不平等和社会不稳定的问题会愈加严重。在工业化初期，解决好剩余劳动力的就业问题，对发展中国家的收入平等和社会稳定有重要意义。

　　马克思理论相对忽略了自然资源限制对经济发展的影响。在人口爆炸式增长的背景下，土地等自然资源约束会导致食品等基础生活物资供应可能会出现短缺。

1.3.2 马克思理论和李嘉图模型的比较

• 相同点：

  • 水平的劳动供给曲线（即劳动供给具有完全弹性）。
  • 工资率为生存水平 \(\overline W\)。
  • 生存水平的工资率是确保资本快速积累的基础。

• 不同点：

  • 劳动供给曲线呈现水平状的原因不同。

    • 马克思理论：工业部门存在未能被雇佣的“剩余劳动力 / 工业后备军”，他们是城市贫民窟中无产者，靠从事非正式活动（例如：小生意、盗窃等）生存，并寻求在工业部门正式就业。因此，只要给予生存水平的工资率，工业部门就可以雇佣到工人。
    • 李嘉图模型：在马尔萨斯人口法则的作用下，工资率的上涨会导致出生率的上升，增加的劳动供给会导致工资率的下降，进而工资率可以保持在生存水平。

  • 工资率上升的情况不同。

    • 马克思理论：当剩余劳动力被工业部门充分吸收后，工资率将高于生存水平 \(\overline W\)。考虑到资本替代劳动的倾向，扩大再生产只会导致更多的失业，即更多的剩余劳动力，因此工资率上升的情况不存在。
    • 李嘉图模型：在短期内，如果人口增长超过了最优等土地的食品生产能力，使用次优等土地导致的要素投入增加会使得食品价格上升，基于食品价格的生存工资率也会上升。但是在长期，工资率将维持在生存水平。

  • 工业部门就业速度与资本积累速度的比较。

    • 马克思理论：形成于 19 世纪中期，蒸汽机驱动的自动机械已经很普遍，固定资产占资本总量的份额提高，因此马克思认为工业就业的增长速度远小于资本积累的速度，资本积累是以牺牲劳动收入份额为代价的。
    • 李嘉图模型：形成于 18 世纪末的工业革命，以蒸汽机为动力源的自动化设备还未得到充分发展，因此李嘉图认为在固定的生存工资率下，就业和资本存量平行增长。

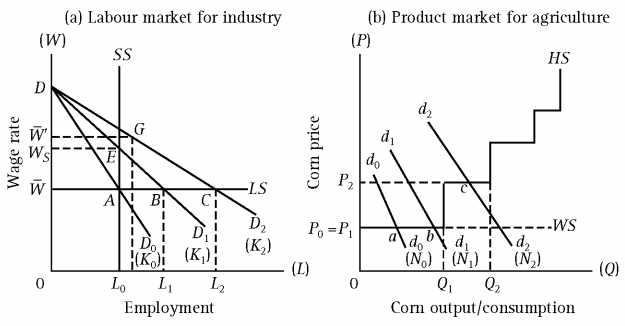
1.4 效率工资理论

　　效率工资理论可以解释马克思模型与新古典经济学存在的几个矛盾点：

• 工业部门存在剩余劳动力，为什么工资率还是一个固定值（生存水平 \(\overline W\)）？
• 为什么存在大量失业和半失业劳动者的就业竞争，资本家不将劳动力的雇佣价格降低至市场出清的水平？

　　效率工资理论基本假设：劳动者的生产效率随着工资的增长而相应增长。资本主义雇主为其雇工提供高于市场出清水平的工资率，且生产率提高的价值增量高于所付工资（大于市场出清水平）的增量。

　　效率工资的两种解释：

• 在低收入国家，市场出清的工资率往往太低，难以满足劳动者家庭的基本营养需求。即便有大量劳动力愿意以更低的工资为雇主工作，雇主也应该支付劳动者足够高的工资用于购买充足的食物。
• 雇主通过支付高于市场出清水平的工资来减少对雇工的监督成本。由于在其他地方工作只能获得市场出清的工资率，挣得多的劳动者害怕失去当前的工作，会更加努力的工作，避免因偷懒、疏忽损害生产设备、偷窃等行为被雇主开出。

　　在第二种关于“监督成本”的解释中，对于劳动者：

\[ \begin{align} z \lt (w-m) p n \end{align} \]

　　其中，\(z\) 表示劳动者通过欺骗产生的预期收益，\(w\) 为雇主目前支付的工资，\(m\) 为被解雇后的预期收入，\(p\) 是欺骗行为被发现的概率，\(n\) 是目前雇佣合同到续约时的周期数。

　　只要上式成立，劳动者的欺骗行为就得不偿失。因此可以算出，雇主支付的最低工资（效率工资）为：

\[ \begin{align} \min \ w=m + \frac z {pn} \end{align} \]

　　在市场出清工资水平 \(m\) 上，雇主可以通过提高工资 \(\frac z {pn}\) 来诱导劳动者尽职工作，或者通过加强监督来提高发现雇工欺骗的概率 \(p\)。如果劳动力的监督成本很高，雇主更加愿意支付更高的工资，而非从市场上招聘监工。

• 当存在大量失业时，市场出清工资水平 \(m\) 很低，通过提高工资减少劳动力监督成本的效果很好。
• 现代工业部门需要培养雇工特定的工作技巧，因此提供的工作往往更正规和更具有长期性。对于雇佣周期 \(n\) 比较长的工作，支付高于市场出清工资率 \(m\) 的效率工资 \(m+ \frac z {pn}\)，比节约出的监督成本更加划算的。

2. 第二次世界大战以来的发展理论和政策

　　以亚当·斯密为代表的古典经济学和马克思经济学都认为，在资本主义市场经济中，压制消费是高资本积累率和经济增长的基础。

　　在第二次世界大战以后，主流发展经济学认为，对于新独立的发展中国家，由于缺乏原始资本积累，市场机制不足以支撑高资本积累率和高增长。该观点以古典假设为基础：在收入处于生存水平时，储蓄率为 0，随着人均收入的增长，储蓄率也会随之增长。

　　在该假设背景下，如果让市场自由配置资源，收入接近生计水平的贫困国家难以跳出低储蓄率和低收入的恶性循环。以行政指令的方式可能是有效的。例如，很多发展中国家倾向于选择社会主义模式，通过中央计划和指令压制消费，或者强制留存一部分资金用于资本积累。

2.1 平衡增长理论

　　第二次世界大战后新独立的发展中国家不太可能依靠初级产品出口的迅速增长来实现经济增长。这些国家只能通过自己制造进口的工业品来实现发展。由于发展中国家的收入低、国内市场狭小，这种工业化战略会受到严重制约，企业生产出的工业品难以被本国消费市场消化。

　　同时发展多种产业，可以互相创造出市场，可以解决发展单一产业导致产品难以销售的问题。多种产业的“平衡增长”需要同时动员大量的资本和劳动力。考虑到发展中国家存在大量隐蔽失业，雇佣这些边际产出为 0 的剩余劳动力可以较好地发展没有较大资金、技术瓶颈的工业化。同时，平衡增长理论认为，发展中国家的工业化缺乏原始资本积累，国内储蓄率低，且难以大规模引进外资，政府建立强制储蓄机制是新独立国家实现经济发展的唯一选择。

2.2 哈罗德-多马模型的应用

　　哈罗德-多马模型（Roy Harrod & Evsey Domar）的基本方程：

\[ \begin{align} g = s /c \end{align} \]

　　其中，\(g = \dot Y / Y\) 为国民收入 \(Y\) 的增长率；\(s = S/Y\) 为储蓄率；\(c= \dot K / \dot Y\) 为边际资本产出比率（资本系数），表示每多生产一个单位的国民收入所需要追加的资本投入。

　　在哈罗德-多马模型中，假设技术水平外生，即边际资本产出比率 \(c\) 为给定的常数，因此，\(c = K /Y\)。上式可以根据凯恩斯均衡假设（投资恒等于储蓄 \(I= \dot K\)）证明得到。

2.3 低均衡陷阱模型

　　低均衡陷阱模型 / 临界的最小努力模型 / 大推进模型：发展中国家的低人均收入和低储蓄率之间存在恶性循环。

　　低均衡陷阱模型的两个基础：1）经济增长完全依赖于有形资本投入的相关模型，2）人口理论

　　图解：

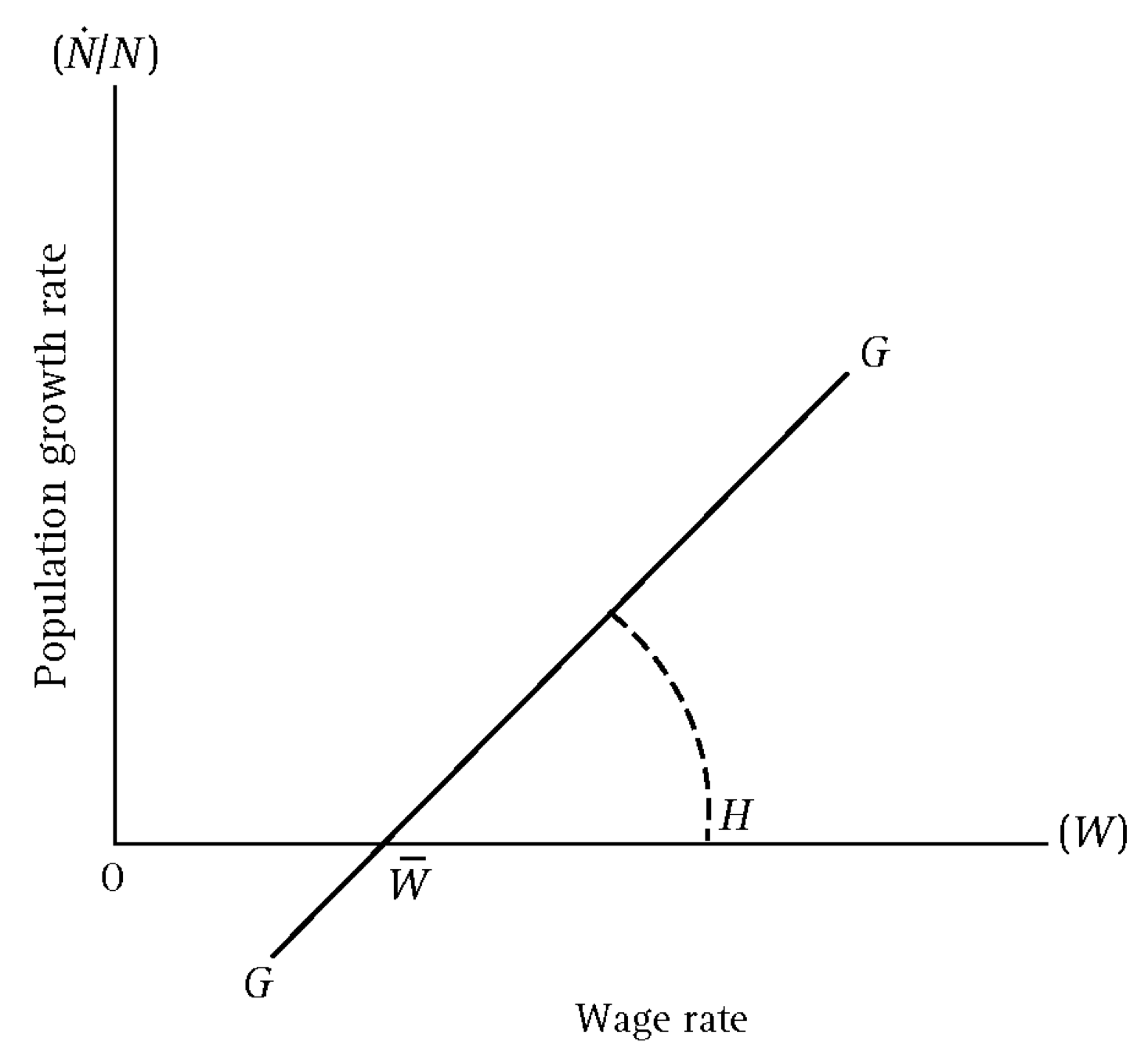
• 图片上面部分：人口增长率 \(\dot N / N\) 和人均收入 \(Y /N\) 的关系。人均收入和工资率是大致成比例的，因此曲线 \(\dot N /N\) 和马尔萨斯人口理论（下方有附图）中的曲线 \(G \overline W H\) 相对应；点 \(m\) 处人口增长率为 0，与生存水平工资率 \(\overline W\) 相对应。

• 图片中间部分：储蓄率 \(s = S/Y\) 和人均收入 \(Y /N\) 的关系。随着人均收入 \(Y /N\) 的提高，\(s\) 呈现指数上升。储蓄率曲线与横轴交于点 \(m\)，此时人均工资率仅为生存水平 \(\overline W\)，劳动者的所有收入用于维持基本生计。

• 图片下面部分：人均收入 \(Y /N\) 与人均收入的增长率的决定因素。人口增长曲线 \(\dot N / N\) 向下移动，储蓄率曲线 \(s\) 与资本产出比率 \(c\) 相除得到的曲线 \(s / c = \dot Y/Y\) 向下移动（这里 \(s / c = \dot Y/Y\) 的计算过程使用了哈罗德-多马模型的基本方程）。图中，点 \(m\) 为稳定的均衡点。

  • 如果人均收入小于均衡点，即 \(\frac Y N \lt m\)，则人口下降速度比总收入下降速度快，人均收入将会增加至 \(m\) 点；
  • 如果人均收入超过均衡点，即 \(\frac Y N \gt m\)，则人口增长率（点 \(b\)）高于总收入增长率（点 \(f\)），人均收入将会下降至 \(m\) 点。

　　位于点 \(m\) 的发展中国家依靠国内投资增加，难以摆脱生计水平的工资率 \(\overline W\)，收入增长会被新增人口分摊掉。

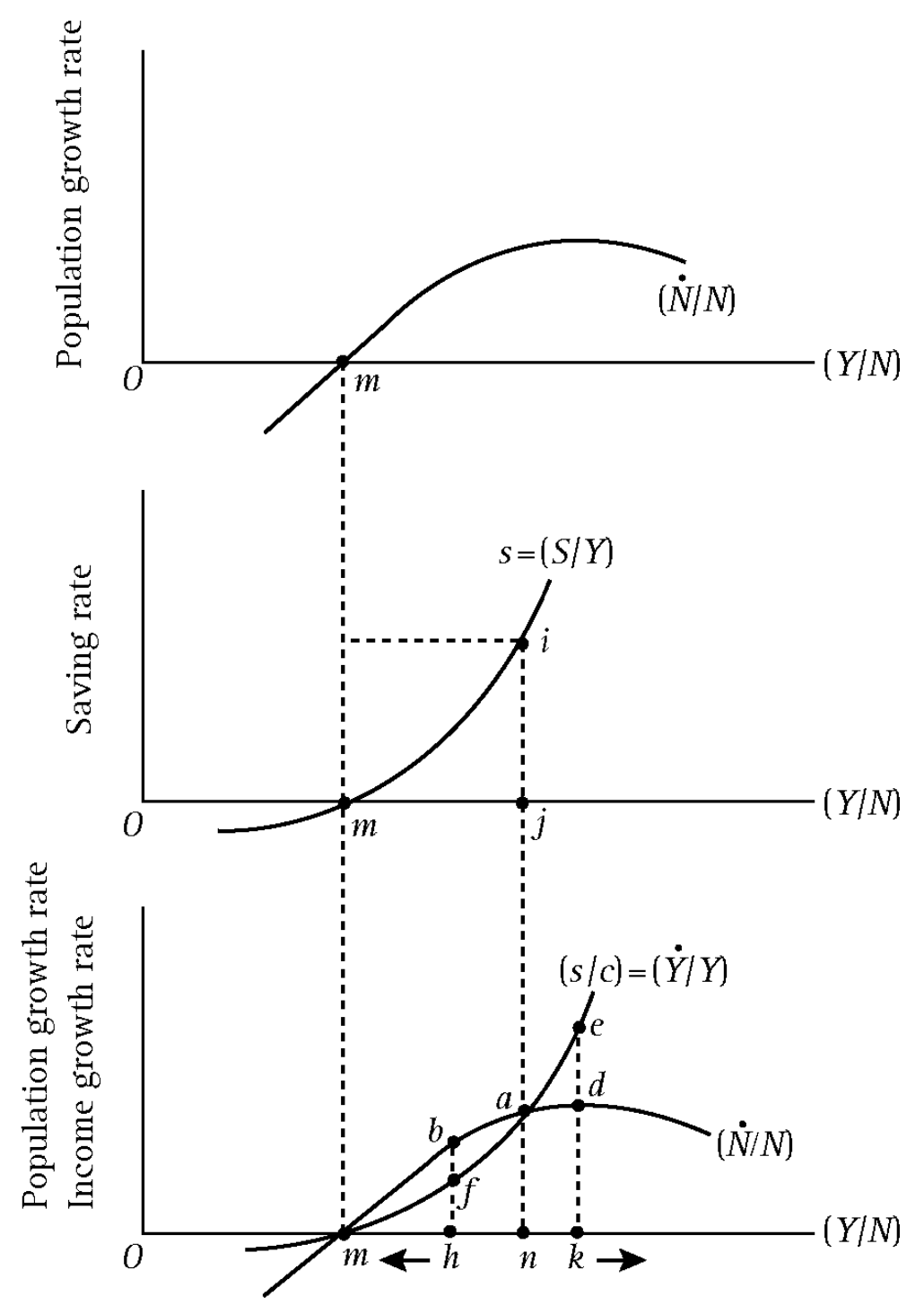
　　因此，依靠一个时期资本积累的适度增长不能跳出低均衡陷阱。为了实现经济持续增长，必须增加足够大的投资，将经济一次性推到 \(n\) 点以上。经济一旦跨越门槛 \(n\)，达到点 \(k\) 处，收入增长率（点 \(e\)）会比人口增长率（点 \(d\)）更高，人均收入的增长才能持续。

　　在低收入国家，依靠市场机制不可能产生储蓄，在动员储蓄和投资时，需要超过“临界最小努力”（点 \(n\)）。因此，新独立的发展中国家不能通过大规模引进资本（例如殖民地时代，通过殖民地的冗余自然资源开发完成原始资本积累），只能从很低的人均收入中强制挤出资本用于原始资本积累。

2.4 发展理论和政策选择

　　许多二战后新独立的国家通过牺牲消费品和服务的生产，来实现原始资本积累，具体政策包括：

• 直接向国有企业投资
• 政府指令性贷款
• 销售管制政策
• 差别税收政策

　　政府实施剥削农业政策（例如：中国的工农业剪刀差），通过农业商品出口税和农产品的高国家垄断收购差价，获得工业资本积累。农产品的低价格抑制了农民的收入和消费，同时降低了工人的生活费用和生存工资率，进而提高了资本利润和投资激励。

　　二战以后，新独立的发展中国家依靠计划经济实现资本积累的原因：

• 在前苏联和其他社会主义国家，全面推行依靠政府命令和计划提高资本积累，20 实际 60 年代前苏联的经济出现了高增长率；
• 发展中国家认为市场经济是殖民政府留下的一种剥削机制。

　　作者的观察和结论：通过政府民工和计划进行资本积累，并没有给发展中国家带来高经济增长率。

3. 新古典生产函数和增长模型

3.1 生产函数的不同假设

3.1.1 哈罗德-多马模型的生产函数

　　在基于特定生产函数形式的经济体中，通过强制手段提高储蓄率可以促进经济增长。与哈罗德-多马模型中的资本产出率 \(c=K/Y\) 相类似，总产出 \(Y\) 与生产要素投入相关的加总生产函数可以表示为：

\[ \begin{align} Y=AK \end{align} \]

　　其中，\(A=\frac 1 c\)，为一个常数。由于经济中存在边际生产率为 0 的剩余劳动力，除非增加更多的资本，否则劳动力的供给增加也无法提高总产出 \(Y\)。在劳动力无限供给、资本相对稀缺的极端情况下，劳动和资本的投入不再具有替代性。

补充：

上面生产函数哈罗德-多马模型下列昂惕夫（Leontief）生产函数的特殊形式。常规形式是：

\[ \begin{align} Y= \min \{ AK, BL \} \end{align} \]

上式表明，在恒为常数的资本生产率 \(A= Y /K\) 与劳动生产率 \(Y/L\) 下，\(AK\) 与 \(BL\) 中的较小的一个决定了实际产出 \(Y\)。如果其中任意一种生产要素固定，另一种生产要素超过了临界 \(K/L\) 的比例，继续增加生产要素供给不会使得产出增加。

在哈罗德-多马模型中，此种情况是一种短期情况，在既定的技术水平下，工厂的机械设计要求配置特定比例的劳动力，固定生产要素投入比例的假设是合适的。在长期中，资本和劳动均可以实现灵活配置，技术水平也会出现重大进展，所以固定生产要素的比例不再合适。

对应劳动力无限供给、资本相对稀缺的情况，也可以假设劳动力供给短缺，拥有大量闲置资本（因此资本边际生产率为 0）的情况，此时生产函数为：

\[ \begin{align} Y= BL \end{align} \]

　　对于发展中国家来说，如果经济存在隐蔽失业的现象，使用 \(Y=AK\) 来衡量要素投入和产出的关系是合适的。但一些学者认为不存在边际劳动生产率为 0 的剩余劳动力（T. W. Schultz, 1964；Hopper, 1965）。

补充：《刘易斯农业零值劳动假说的“自然实验” 检验：来自印度大流感与中国大跃进的证据》

舒尔茨（Schultz）在《改造传统农业》中指出，零值劳动力假说建立在不完全的要素市场和有限的技术替代性基础上，并使用印度 1918-1919 年大流感的经验资料来验证这一观点。印度爆发大流感导致劳动力数量下降了约 8%，在大流感爆发后，谷物播种面积则减少了 3.8%，该测算结果与产量对劳动的弹性大致接近。舒尔茨据此认为，在以印度为代表的贫穷农业国，不存在零值劳动力，劳动力数量的下降会导致播种面积（进而农业产出）成比例的下降。

不过舒尔茨的分析主要使用二手资料，并大量引用了其他学者的测算数据，不同来源、不同测算口径的数据的可比性不够高，是一些学者认为舒尔茨批评零值劳动力假说证据不足的原因之一。

　　在长期分析中，技术水平 \(A=\frac 1 c\) 是一个常数的假设可能不再适用。根据哈罗德的分析，当利率外生（固定）时，使资本产出比率 \(K/Y\) 不变的技术进步为哈罗德中性技术进步（相当于希克斯的劳动节约型）。因此，哈罗德-多马模型认为，只有通过技术进步，才能降低资本产出比率 \(K/Y\)。

补充：

哈罗德中性技术进步是比较符合经济现实的一种技术进步。对于生产函数 \(Y=F(K,AL)\)，其假设如下：

假设一：相对于资本、劳动和知识，其他投入要素不重要（生产函数中不包括其他的生产要素）。

假设二（关键假设）：生产函数对两个自变量（资本和有效劳动）是规模报酬不变的。即：

\[ \begin{equation} F(cK,cAL)=cF(K,AL), \ \ \forall c \ge 0 \end{equation} \]

可以得到： \(F(\frac K {AL},1)=\frac 1 {AL} F(K,AL)\)，其中 \(AL\) 为考虑技术效率的有效劳动。

哈罗德中性 / 劳动节约型 / 劳动增进型技术进步：对于固定不变的资本产出比率 \(K/Y\)，技术进步体现为对劳动生产率的提高，或者说是对劳动的替代。也就说，资本 \(K\) 和有效劳动 \(AL\) 同时成倍增加，会使得经济产出 \(Y\) 以相同的倍率增加，此时资本 \(K\) 和有效劳动 \(AL\) 的投入比例 \(\frac K {AL}\) 不变，但资本 \(K\) 和劳动 \(L\) 投入的比例 \(\frac K L\) 已经发生，技术进步（即技术效率 \(A\) 的提高）意味着劳动雇佣量 \(L\) 的减少。

3.1.2 新古典生产函数

　　在特定的生产技术 \(T\) 下，劳动 \(L\)、资本 \(K\) 两种生产要素与产出 \(Y\) 的关系：

\[ \begin{align} Y= F(L,K;T) \end{align} \]

　　生产函数的假设：生产函数二次可微，且满足稻田条件，即一阶导数大于 0，二阶导数小于 0，\(L\) 和 \(K\) 的交叉导数大于 0。假设 \(T\) 的变化会影响 \(L\) 和 \(K\) 的导数。

　　特殊情况：柯布-道格拉斯生产函数：

\[ \begin{align} Y= AL^{\alpha } K ^{\beta} \end{align} \]

　　其中，\(\alpha\)、\(\beta\) 分别是劳动和资本的产出弹性，表示分别增加 1% 的劳动 \(L\) 或资本 \(K\)，产出相应增长的百分比。技术 \(A\) 表示给定劳动 \(L\) 资本 \(K\) 组合时决定产出的技术。

　　假设 \(\alpha + \beta =1\)，如果劳动 \(L\) 和资本 \(K\) 同比例增长，\(Y\) 也按照同样的比例增长（线性齐次特性）。

　　哈罗德-多马模型是柯布-道格拉斯生产函数的特殊形式（\(\alpha = 0, \ \beta =1\)）。

　　如果柯布-道格拉斯生产函数有 \(0 \lt \alpha , \ \beta \lt 1\)，\(\alpha + \beta =1\)，那么就可以得到：

• 劳动 \(L\) 和资本 \(K\) 可以互相替代
• 随着投入增加，要素的边际生产率递减

3.2 索洛-旺斯模型

　　在线性齐次生产函数 \(Y= AL^{\alpha } K ^{\beta}\) 中，两边分别除以 \(L\)：

\[ \begin{align} y= A k ^{\beta} \end{align} \]

　　其中：\(y=Y/L\) 为劳均产出，\(k=K/L\) 为劳均资本投入。

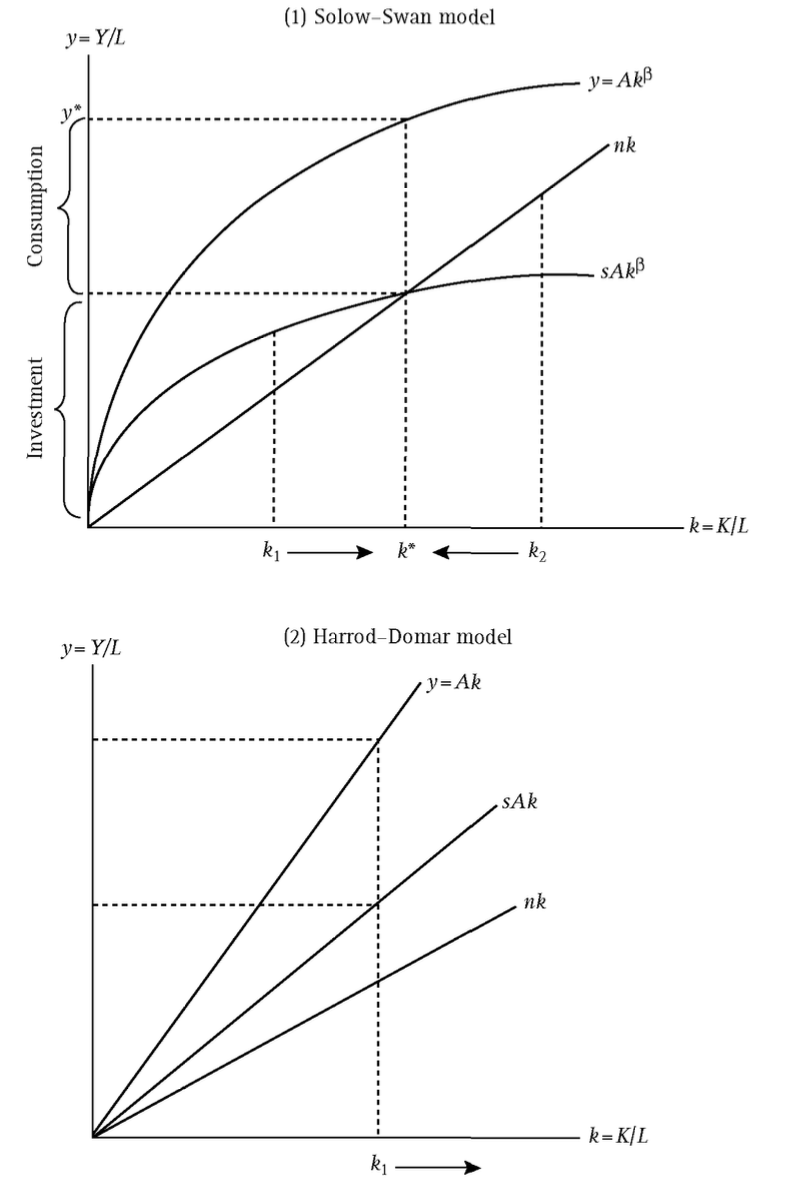
　　假设在一年内，平均储蓄率为 \(s\)，劳均储蓄为 \(sy\)。由于投资储蓄恒等式，劳均储蓄 \(sy\) 和劳均投资相等。如果劳动力投入数量不变，那么劳均资本增长率为 \(\frac {sy} k\)。在发展中国家，由于劳动力数量增加，会导致劳均资本增长率下降。对于劳均资本投入 \(k=K/L\)，先做对数运算，再对时间进行微分可得：

\[ \begin{align} \frac {\dot k} k= \frac {\dot K} K - \frac {\dot L} L \end{align} \]

　　其中：资本增长率 \(\frac {\dot K} K = \frac {sY} K=\frac {sy} k\)，假设人口增长率和劳动生产率相等 \(n=\frac {\dot L} L\)，那么：

\[ \begin{align} \frac {\dot k} k= \frac {sy} k - n \end{align} \]

　　上式中，资本存量为扣除折扣后的净资本存量。将上式左右两边乘以 \(k\)，可得：

\[ \begin{align} \dot k= sy - nk = s A k ^{\beta}- nk \end{align} \]

　　上式中，\(sAk^{\beta}\) 为劳均收入中用于消费的部分，\(nk\) 为斜率为 \(k\) 的直线（如上图的上半部分）。

• 当 \(s A k ^{\beta} = nk\) 时，此时达到均衡状态，均衡劳均资本为 \(k ^*\)，劳均资本的增长率 \(\dot k= 0\)；
• 当 \(s A k ^{\beta} \gt nk\) 时，此时劳均资本为 \(k_1 \lt k ^*\)，由于劳均资本的增长率 \(\dot k \gt 0\)，劳均资本会增长 \(k_1 \to k^*\)；
• 当 \(s A k ^{\beta} \lt nk\) 时，此时劳均资本为 \(k_1 \gt k ^*\)，由于劳均资本的增长率 \(\dot k \lt 0\)，劳均资本会下降 \(k_2 \to k^*\)。

　　因此，劳均产出 \(y\) 最终将会收敛于均衡产出 \(y^* = A {k^*} ^{\beta}\)。当达到稳态时：

• 净资本存量 \(K\) 和总产出 \(Y\) 按相同的速率增长，为人口增长率（\(\frac {\dot K} K = \frac {\dot Y} Y=n\)）。
• 如果储蓄率 \(s\) 提高，或者人口增长率 \(n\) 下降，曲线 \(s A k ^{\beta}\) 和直线 \(nk\) 的交点会移动至 \(k^*\) 右边，在 \(k^*\) 的水平上，\(s A k ^{\beta}- nk \gt 0\)，因此劳均产出 \(y\) 和劳均资本存量 \(k\) 向新的稳态移动。达到新的均衡后，经济增长将会停止。
• 只有持续的技术进步 \(A\)，才可以继续提高劳均产出 \(Ak^{\beta}\)，实现劳均产出的增长。

　　在哈罗德-多马模型中，生产函数为一条直线：

• 如果 \(sA \gt n\)，即 \(\dot k \gt 0\)，劳均资本 \(k\) 可以实现无限增长；
• 如果 \(sA \lt n\)，即 \(\dot k \lt 0\)，劳均资本 \(k\) 将持续降低，将会陷入低均衡陷阱（对应低均衡陷阱模型中 \(m \to n\) 部分）；
• 通过强制手段抑制消费、提高储蓄率 \(s\)，使得 \(sA \gt n\)，就可以实现持续的经济增长。

　　在索洛-斯旺模型中，生产函数为一条凸曲线：

• 提高储蓄率产生的影响时暂时的，对经济增长的影响只能持续到新的稳态为止；
• 如果没有持续的技术进步，人均收入（劳均产出）的提高不能持续，经济无法实现持续增长。

4. 增长核算检验

　　新古典增长模型认为技术进步是持续经济增长的关键因素，提高储蓄率对经济增长则是短期影响。但如果储蓄率能达到 5%~10%，这种短期的经济增长也可能持续相当长的是时间。增长核算分析可以用以分析“与技术进步相比，提高储蓄率对资本和产出的影响有多大”这一问题。

4.1 增长核算方程

4.1.1 生产函数形式

　　为了考察经济增长的源泉，区分经济增长的直接原因和基本原因，提出以下方程：（宏观经济学第 8 章-经济增长）

\[ \begin{align} Y_t=f(K_t, R_t, N_t, A_t, B_t) \end{align} \]

• \(Y_t\)：经济的总产出；
• \(K_t\)：资本存量；
• \(R_t\)：自然资源；
• \(N_t\)：劳动投入；
• \(A_t\)：经济应用知识的储量；
• \(B_t\)：基本因素，或“社会文化环境”或“社会能力”，是经济运行所不可缺失的。

　　对上面的生产函数进行简化，假设希克斯中性形式的生产函数为：

\[ \begin{align} Y=AF(L, K) \end{align} \]

　　其中，经济总产出 \(Y\) 由劳动 \(L\) 和资本 \(K\) 投入生产出来，且技术进步同时作用于资本和劳动，由初期确定的 \(L\) 和 \(K\) 生产的产出，会随着技术进步增加 \(A\) 倍。假设该生产函数为乘法形式，且对于资本 \(K\) 和劳动 \(L\) 投入，具有规模报酬不变、线性齐次的的性质（例如：\(Y=A L^{\alpha} K^{\beta}\)，其中 \(\alpha +\beta =1\)）。

　　对上述的生产函数取对数，然后对时间 \(t\) 作微分，可得：

\[ \begin {align} g_Y=g_A+\alpha g_L + \beta g_K \end {align} \]

• \(g_Y\)：总产出增长率，\(g_Y = \dot Y / Y\)；
• \(g_A\)：技术增长率（全要素生产率），\(g_A = \dot A / A\);
• \(g_L\)：劳动增长率，\(g_L = \dot L / L\)；
• \(g_K\)：资本增长率，\(g_K = \dot K / K\)。

4.1.2 产出弹性与索洛余量

　　其中，\(\alpha\) 和 \(\beta\) 分别为劳动和资本的产出弹性（劳动和资本增长 1% 时，产出增长的百分比）：

\[ \begin {align} \alpha = \frac { \partial Y / \partial L } {Y / L} \ ; \ \ \beta = \frac { \partial Y / \partial K } {Y / K} \end {align} \]

　　与柯布-道格拉斯生产函数的区别：

• 柯布-道格拉斯生产函数：\(\alpha\) 和 \(\beta\) 为常数，因为技术外生；
• 增长核算方程：\(\alpha\) 和 \(\beta\) 可以发生变化。

　　索洛余量：产出增长率 \(g_Y\) 中不能被资本 \(\beta g_K\) 和 \(\alpha g_L\) 劳动增长率贡献解释的部分，是扣除 \(L\) 和 \(K\) 影响后产出 \(Y\) 增长的残差。

\[ \begin {align} g_A=g_Y - \alpha g_L - \beta g_K \end {align} \]

4.1.3 人均产出与劳均产出的增长核算方程

　　在要素市场处于竞争性均衡的假设下，劳动和资本的收入份额分别为 \(\alpha\) 和 \(\beta\)，即：\(\alpha = \frac {wL} {Y}\)，\(\beta = \frac {rK} {Y}\)。此时，均衡工资率 \(w\) 为劳动的边际产出 \(w=\frac {\partial Y} {\partial L}\)，均衡利率 \(r\) 为资本的边际产出 \(r=\frac {\partial Y} {\partial K}\)。

　　真实的经济会在一定程度上偏离竞争性均衡，由于生产弹性难以计算，用要素份额代替生产弹性，增长核算分析的结果误差是不可避免的。

4.1.3.1 人均产出的增长核算方程

　　在上面增长核算方程的基础上，两边同时减去人口增长率 \(g_N\)（\(g_N = (\alpha +\beta ) g_N\)，因为假设规模报酬不变 \(\alpha +\beta =1\)），可以得到人均收入的增长核算方程：

\[ \begin {align} g_Y -g_N & = g_A+\alpha (g_L -g_N) + \beta (g_K -g_N) \\ \notag & = g_A+\alpha g_{ (L /N)} + \beta g_{ (K /N)} \end{align} \]

　　上式可以改写为：

\[ \begin {align} g_{ (Y/N) } =g_A+\alpha g_{ (L/N) } + \beta g_{ (K/N) } \end{align} \]

　　其中：\(g_{ (Y/N) }\) 为人均产出增长率；\(g_{ (L /N)}\) 为劳动力占比增长率；\(g_{ (K /N)}\) 为人均资本增长率。

4.1.3.2 劳均产出的增长核算方程

　　与上面人均产出增长核算方程类似，在原始的增长核算方程的基础上，两边同时减去劳动增长率 \(g_L\)（\(g_L = (\alpha +\beta ) g_L\)，因为假设规模报酬不变 \(\alpha +\beta =1\)），可以得到劳均收入的增长核算方程：

\[ \begin {align} g_Y -g_L & = g_A+\alpha (g_L -g_L) + \beta (g_K -g_L) \\ \notag & = g_A+ \beta g_{ (K /L)} \end{align} \]

　　上式可以改写为（字母的含义发生了变更）：

\[ \begin {align} g_{ (Y/L) } =g_A + \beta g_{ (K/L) } \end{align} \]

　　其中：\(g_{ (Y/L) }\) 为劳均产出增长率；\(g_{ (K /L)}\) 为劳均资本增长率。

4.2 现代经济增长的源泉

　　总产出、人均产出、劳均产出的增长核算方程：

\[ \begin {align} & g_A =g_Y - \alpha g_L - \beta g_K \\ & g_{ (Y/N) } =g_A+\alpha g_{ (L/N) } + \beta g_{ (K/N) } \\ & g_{ (Y/L) } =g_A + \beta g_{ (K/L) } \end {align} \]

　　库兹涅茨（Kuznets, 1966）的结论：发达工业国的经济增长（以人均收入 \(Y/N\) 衡量）来源主要是全要素生产率的增长。全要素生产率对实际收入增长的贡献远比要素投入的贡献重要。

　　（1）使用人均产出估计：

　　发达的在 18 世纪 50 年代支 19 世纪 50 年代（50-100 年里），发达工业国的世纪人均收入（人均产出）年增长率为 1%～2%，年平均增长率为 1.5%，人均工作小时数每年下降约 0.3%。在整个过去的 50-100 年内，资本产出比率下降约 30%，劳动产出比率约占 70%，即人均资本增长率为 \(g_{ (K/N) } = 1.5 \% \times 0.7 \approx 1 \%\)。发达国家中劳动和资本收入份额一般为 \(\alpha = 0.75\) 和 \(\beta = 0.25\)。

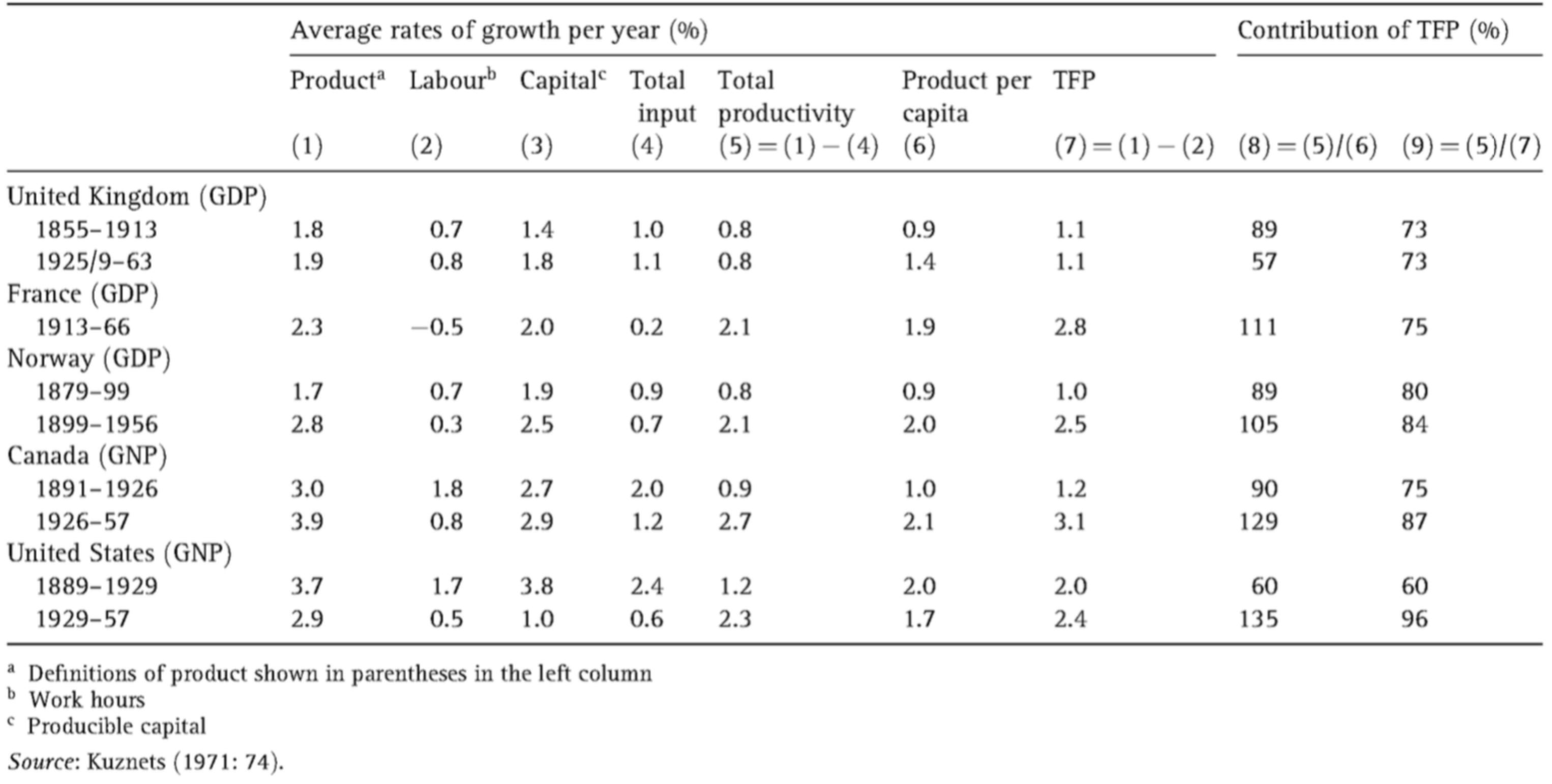
　　因此，资本对人均收入增长的贡献为 \(\beta g_{ (K/N) } = 0.25 \times 1.0 \% = 0.25 \%\)，仅为人均收入平均增长率（1.5%）的 17%；劳动对人均收入增长贡献为 \(\alpha g_{ (L/N) } = 0.75 \times (-0.3 \%)=-0.23 \%\)。

　　劳动和资本对人均收入增长贡献合计仅有 \(\beta g_{ (K/N) } + \alpha g_{ (L/N) } = 0.25 \% + ( - 0.23 \% ) = 0.02 \%\)，因此，实际人均收入增长的 99% 都是由全要素生产率 \(g_A\) 增长带来的。

　　（2）使用劳均产出估计：

　　资本产出比率对劳动生产率增长的贡献仅有约 20%，全要素生产率的贡献约有 80%。

5. 经济增长类型的变化

　　库兹涅茨将工业革命以来西方发达国家的经济增长解释为持续的技术进步，而非资本积累。随着技术水平的迅速提高，资本积累带来的边际报酬递减问题会被克服，从而会导致资本产出比例 \(K/Y\) 的下降。

　　但是在全要素生产率快速上升以前，技术进步可能并不能很好地解释经济增长。

5.1 增长核算的历史延申

　　Abramovitz（1993）的观点：从 19 世纪初开始，工业化初期的经济增长是以资本积累为基础的，而非技术进步。

　　图下图所示，在发展早期（1800-1855 年、1855-1900 年），资本-劳动比率增长 \(g_{ (K/L) }\) 的贡献远远大于全要素生产率 \(g_A\) 的贡献，资本的产出比率 \(K/Y\) 增加了，资本的收入份额也有大幅增加（从 0.34 增加到 0.45），这符合马克思的资本主义经济发展理论。

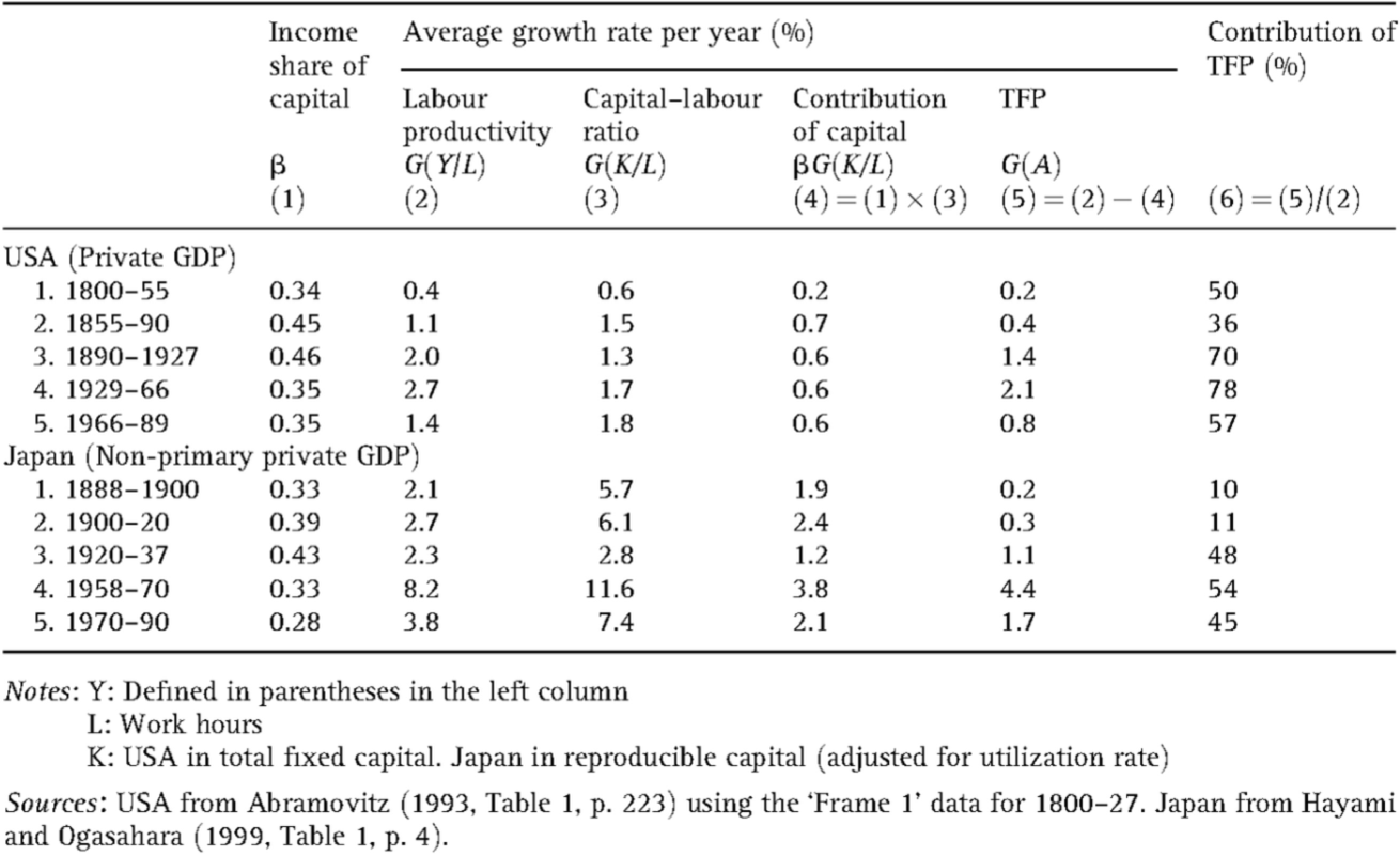
　　美国的经济增长可以划分为以下几个阶段：

• 第一阶段（1800-1855 年）：初级工业化阶段，马克思类型，经济增长以资本-劳动比率的贡献为主导。
• 第二阶段（1855-1890 年）：高级工业化阶段，马克思类型，经济增长以资本-劳动比率的贡献为主导。
• 第三阶段（1890-1927 年）：库兹涅茨类型，经济增长以全要素生产率提升的贡献为主导。
• 第四阶段（1927-1966 年）：库兹涅茨类型，经济增长以全要素生产率提升的贡献为主导。
• 第五阶段（1966-1989 年）：马克思类型和库兹涅茨类型的混合类型，国家进入“后工业社会”，全要素生产率的增长贡献约为 50%。

　　在新生的工业经济达到成熟之前（第一、第二阶段），美国经济出现了同马克思增长类型相似的阶段。在工业经济成熟以后（第三、第四阶段），马克思增长类型将转化为库兹涅茨类型。

　　与美国类似，日本也出现了相似的经济阶段划分：

• 第一阶段（1888-1900 年）：初级工业化阶段，马克思类型，资本-劳动比率的增长率比实际劳动生产率的增长率高，资本-产出比率增长，经济增长的主要来源是资本-劳动比率的增长。
• 第二阶段（1900-1920 年）：高级工业化阶段，马克思类型，资本-劳动比率的增长率比实际劳动生产率的增长率高，资本-产出比率增长，经济增长的主要来源是资本-劳动比率的增长。
• 第三阶段（1920-1937 年）：开始从马克思类型向库兹涅茨类型过渡，全要素生产率的贡献接近 50%，资本收入份额达到顶峰；资本-劳动比率的增长率继续超过劳动生产率的增长率。
• 第四阶段（1958-1970 年）：马克思类型与库兹涅茨类型的混合类型，经济高速增长，但资本劳动比率的增长超过了劳动生产率的增长，资本-劳动比率继续上升，全要素生产率的增长贡献约为 50%（美国第四阶段为 80%）。
• 第五阶段（1970-1990 年）：马克思类型与库兹涅茨类型的混合类型，国家进入“后工业社会”，全要素生产率的增长贡献约为 50%。

　　一个国家的发展历程中，资本产出比率会出现“倒 U”型变化，在人均收入达到一个门槛之前呈现上升趋势，随后呈现下降趋势。

5.2 马克思增长类型的陷阱

　　在二战后新独立的发展中国家中，许多都选择了通过中央计划经济的方式实现资本积累，进而推动国家工业化和经济发展。但是，许多通过中央计划经济的国家（例如：前苏联）都陷入了马克思增长类型的陷阱，即马克思增长类型向库兹涅茨类型的转型失败。马克思增长类型陷阱也被称为中等收入陷阱。

5.2.1 前苏联的案例

　　上面的分析表明，美国和日本都有能力从以资本积累为基础的马克思增长类型，转向以提高全要素生产率为基础的库兹涅茨增长类型。随着类型的变化，资本的收入份额越来越小，而劳动的收入份额越来越大，这意味着收入分配平等的提高。

　　增长类型的变化（马克思 \(\to\) 库兹涅茨）并不是一定会发生的。由于在中央计划体制中缺乏要素市场，所以应用在资本上的固定权重，是对资本生产弹性的非正式推测。

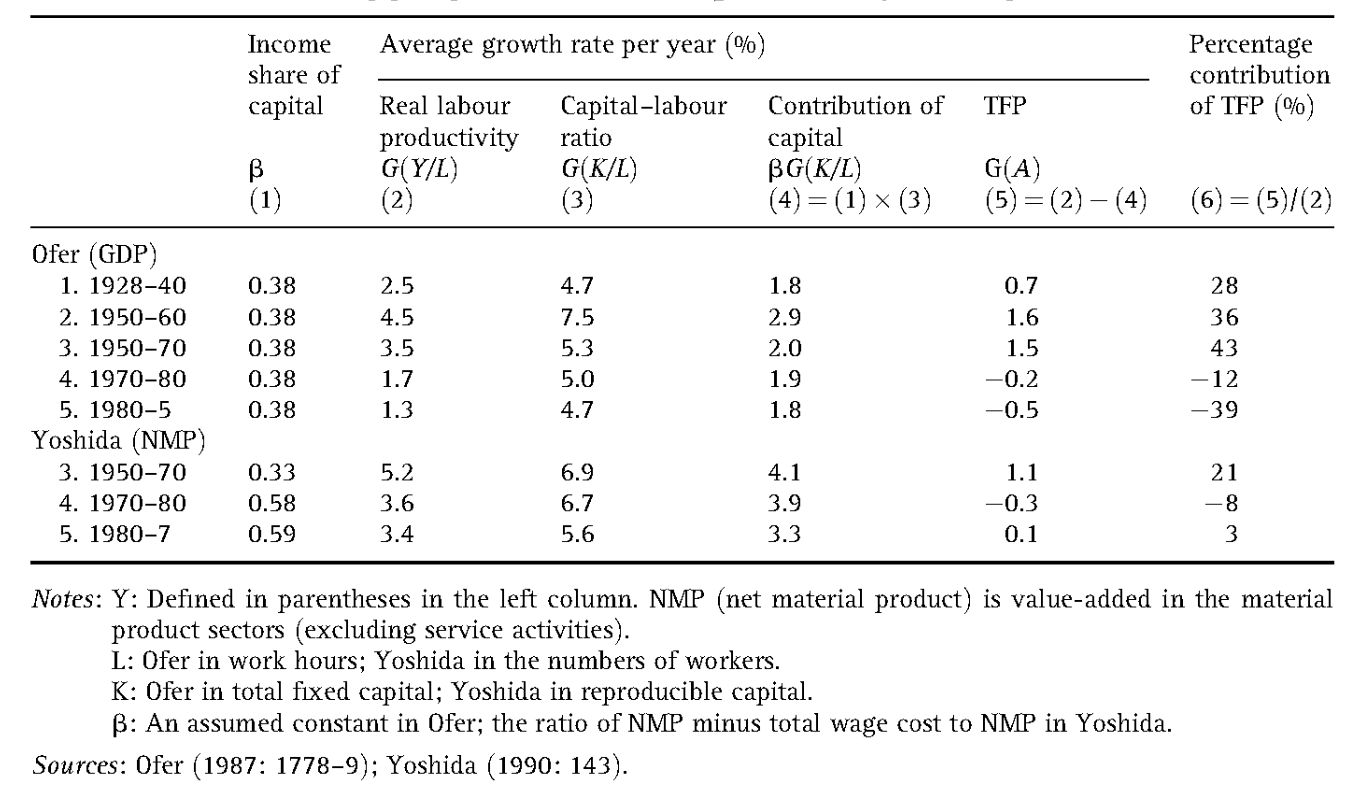
　　苏联的计划经济是在政府指令下最大限度地积累资本以推动经济的极端情形。这种推动方式的结果：

• 资本-劳动比率的增长率远远大于发达的市场经济国家；
• 第一、第二阶段（从两次世界大战以来一直到 20 世纪 60 年代）：与美国、日本比较相似，为马克思增长类型。劳动生产率的增长率很高；资本-劳动比率的增长远远超过劳动生产率增长，即资本产出比率不断提高；全要素生产率的贡献大约为 30%～40%。
• 第三、第四、第五阶段（20 世纪 60 年代以后）：马克思增长类型向库兹涅茨类型转型没有成功。全要素生产率增长低于劳动生产率增长，且在 20 世纪 70 年代以后，全要素生产率出现了负值。前苏联因资本边际报酬严重下降而陷入困境，同时迅速积累的资本是在几乎没有技术进步的情况下应用到生产过程中的。

5.2.2 原因

　　中央计划经济导致陷入马克思增长类型陷阱的原因，可能和已经完成初级工业化并正在进入高级发展阶段的中等收入国家的政策选择相关。

　　假定增长核算中资本扩张型技术进步，并采用超越对数生产函数。

　　东亚新兴工业化经济（包括韩国、台湾、香港、新加坡）的资本生产弹性非常高，但全要素生产率增长对劳动生产率增长的相对贡献变化趋势正好相反。在发达国家中，日本类型和新兴工业化经济最为接近，即马克思增长类型通常会出现在工业化初期，并且会在那些发展模式更加依赖“引进转移”的工业化开始晚的国家中持续更长的时间。

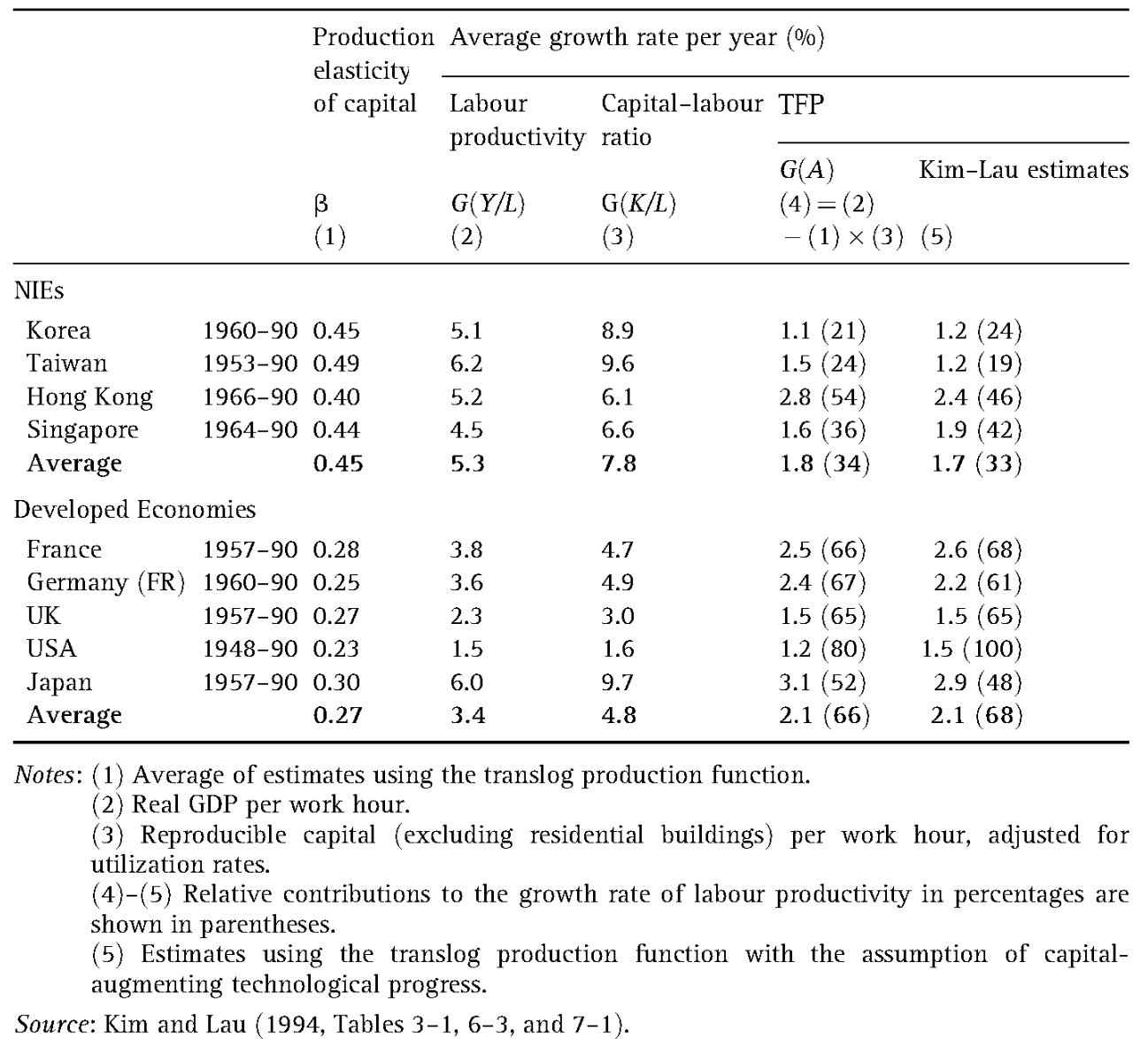
补充：

当前中国处于产业升级的关键阶段。长期以来，我国主要实行引进技术、消化、吸收的方式追赶与发达国家的技术差距。然而，拿来主义的技术发展模式会陷入瓶颈，在越南、印度等国依靠成本优势吸引大量初级和中端制造业外流的情况下，如果无法实现高端产业技术的突破，无法通过技术创新获得高收入来源，那么就会陷入“中等收入陷阱”。具体体现为在发展为中等收入国家后，由于成本竞争优势下降和技术进步受阻，无法同低收入国家和发达国家竞争，经济发展停滞于中等收入国家水平。

二、技术进步的类型与源泉

　　在经济开始工业化发展的早期，经济增长主要依赖资本积累，此阶段的经济增长往往伴随着收入分配不平等的加剧，与马克思所描述的资本流向资本家手中、用于资本积累的资本主义经济的特征比较相似。而在工业化的高级阶段，广义上的技术进步（包括改进投入品质量的作用）对经济增长的贡献远远大于有形资本积累的贡献，此阶段资本收入份额将会下降，收入分配不平等程度将会降低。

1. 马克思与库兹涅茨的经济增长类型比较

　　在工业化发展过程中，可以分为两个阶段：

• 阶段 1：马克思阶段（Marx Pattern）
• 阶段 2：库兹涅茨阶段（Kuznets Pattern）

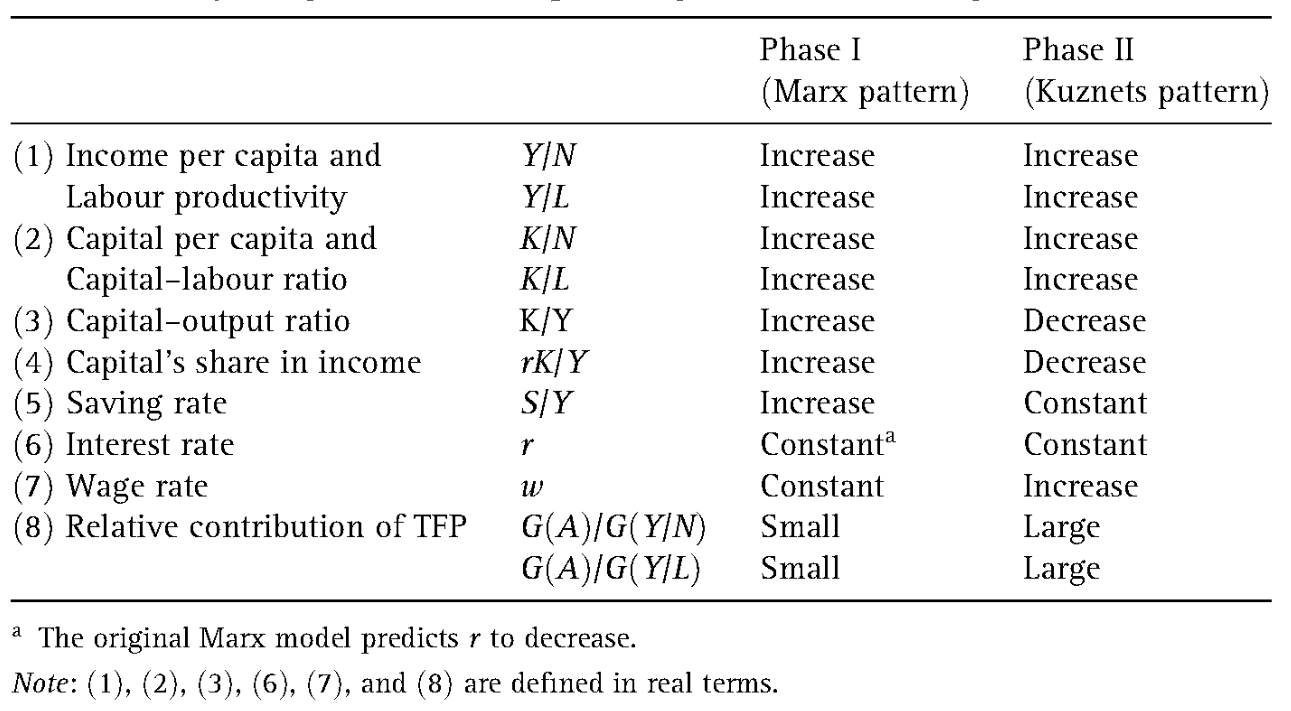
1.1 马克思阶段

• 在资本主义发展过程中，不变资本（购买非劳动力投入的资金）要比可变资本（购买劳动力投入的资金）积累地更快，利润或“剩余价值”只能来自对劳动力的剥削，因此资本报酬率将会下降。
• 利润相对于资本投入总量的下降并不是资本有机构成（不变资本占总资本的比率）提高所不可避免的后果，如果剩余价值率能随着技术进步或者其他原因提高，以至于能阻止资本有机构成的上升，利润率可以保持不变。
• 如果资本的报酬率下降的非常快，就有可能违背马克思关于资本收入份额增加的预见。

　　马克思理论的新古典解释：在资本-劳动比率迅速上升的条件下，技术进步中劳动节约型的偏向有可能维持甚至提高资本报酬率（传送门：附录A2 - 技术变化的分类）。

　　在修正的马克思类型中的要素价格：

• 假定了马克思类型的利率 \(r\) 固定不变，但利率 \(r\) 有可能会适度下降。
• 假定生存水平实际工资率 \(w\) 不变，但生存水平的实际工资率 \(w\) 可能会适度上升。
• 如果资本和劳动的价格发生适度变化，即相对要素价格（工资利率比率）\(w/r\) 可能略微增长，要素相对价格的相对增长幅度一定小于资本劳动比率 \(K/L\) 的增长率，所以资本的收入份额 \(rK/Y\) 是上升的。

1.2 马克思阶段与库兹涅茨阶段的比较

　　如果相对要素价格 \(w/r\) 增长速度较快，且快过资本劳动比率 \(K/L\) 的增长率，那么资本收入份额 \(rK/Y\) 下降，此时属于库兹涅茨类型。

　　相同点：

• 人均国民收入 \(Y/N\)、劳均国民收入 \(Y/L\)、人均资本存量 \(K/N\)、资本-劳动比率 \(K/L\) 都是具有上升趋势

　　不同点：

　　在马克思类型中：

• 人均资本存量 \(K/N\)、资本-劳动比率 \(K/L\) 的增长分别快于人均资本存量 \(K/N\)、资本-劳动比率 \(K/L\) 的增长。即生产函数没有随着劳均资本量的增加而移动或者移动较小，此时资本报酬递减。
• 全要素生产率对人均收入和劳均收入的贡献小。
• 资本劳动比率 \(K/L\) 上升，且资本的收入份额也上升，属于希克斯定义的劳动节约型技术进步。
• 收入大堆集中在资本家手中，发展中国家的储蓄率上升并不来自工资率的上升，而是资本家的剥削和资本积累。除非开发出使用资本倾向的技术，使资本的报酬率保持在比较高的水平，否则高储蓄率不能维持下去。

　　在库兹涅茨类型中：

• 人均资本存量 \(K/N\)、资本-劳动比率 \(K/L\) 的增长分别慢于人均资本存量 \(K/N\)、资本-劳动比率 \(K/L\) 的增长；资本报酬递减被生产函数的较大移动而克服了。
• 全要素生产率对人均收入和劳均收入的贡献大，因此生产函数可以实现较大的移动。
• 资本劳动比率 \(K/L\) 上升，由于替代弹性小于 1，资本收入份额下降，因此属于资本节约型技术进步。
• 由于工资率上升速度比利率上升速度更快，因此储蓄主要来自工资上涨后工人的消费剩余，反映了中等收入的劳动阶级随着工资收入的持续上升而具有储蓄的倾向。

2. 两种增长类型的技术条件

2.1 类型转变机制

　　马克思类型向库兹涅茨增长类型转变的机制：

• 工业技术体制由常规技术变为微观技术；
• 人们的需求从标准化产品转变为有差异的产品。

　　（1）工业技术体制的变化

　　在第二阶段，要避免资本报酬率下降，需要加速技术进步，这依赖于科学研究和教育的制度化，即为了改进专业技术的科学研究和教育制度的建立。

　　技术体制的转变，是技术进步的取向由促进有形资本对劳动的替代到促进无形资本对有形资本替代的转变。技术进步的倾向是由有形资本利用、劳动节约型转变为无形资本利用、有形资本节约型。

　　科学的系统应用是现代经济增长中技术进步比以往时代更快、更稳定的因素。

　　要使微观的新技术有效运行，工人的能力必须变化，接收正式教育以看得懂科学和工程手册。

　　（2）需求结构的转变

　　在度过工业化初期以后，随着人均收入的上升，人们的基本需求得到满足，需求将会从标准型产品转向不易实行机械化的有差异的产品。

2.2 工资率与资本收入份额的变化

　　在新的工业技术体制下，与有形资本相比，人的能力和知识的边际生产率急剧上升（例如：信息产业）。与有型资本相比，工资率（简单劳动报酬 + 教育和培训获得的人力资本报酬）会急剧上升，工资-利率比例的上升会超过资本-劳动比率的增长，并导致资本收益份额 \(\frac {rK} Y\) 的下降。

　　在第二阶段人口增长率下降和因人均收入提高引起休闲偏好上升所造成的劳动力供给下降，会加快劳动力工资率的增长。但如果第二阶段的产品需求不发生变化，人力资本积累不够快，第一阶段传统的劳动节约型技术进步就会以足够快的速度继续发展，从而抵消掉劳动力供给减少对工资率增长的促进作用。

2.3 借用技术和马克思类型的增长

　　对于东亚新兴工业化经济体，依靠借用技术追赶发达经济体过程中，有可能出现马克思-库兹涅茨混合类型的。发展中国家往往从发达国家引进资本密集、劳动节约型的先进技术。对于技术引进国而言，国际贸易和国外直接投资会加强劳动节约型技术的应用。

　　根据产品循环理论（Raymond Vernon, 1966），跨国公司或发展中国家的私营企业把产品开发的基地放在新产品市场大、从事研究开发的高素质人力资源禀赋丰富的高收入国家。在产品完成开发以后，经过一系列的市场检验与生产过程标准化，大批量生产会转移到韩国、台湾等发展中的经济体，因为台湾和韩国等地区有大量受过相对良好教育、工资水平低的劳动管理可供使用。完成产品生产后，将产品出口到发达国家。

　　产品循环理论本质是全球分工，发达的工业国将高密度的人力资本投入到产品的研究和开发，新兴工业化经济体则使用价格低廉的劳动力和劳动节约型技术开发的自动机械生产标准化产品。

　　在第二次世界大战期间，日本和美国的技术差距扩大了；在战后，日本被美国全面接管，借用美国的技术成了日本最有利的选择，因此在第四阶段（1958年）以后（本章第5节“增长核算的历史延申”部分），日本的经济增长为马克思和库兹涅茨的混合类型。

3. 寻求技术进步源泉

　　技术进步是经济增长的速度和类型的主要决定因素，技术进步的源泉是对人知识和能力的投资（无形资本积累）。

　　本节关注的问题：为了促进技术进步，什么样的制度框架有助于提高投资配置的效率？

3.1 全要素生产率增长的原因

　　在线性齐次生产函数的假设下，用简单的增长核算度量的全要素生产率的增长，是产出增长中不能使用常规投入（主要是资本、劳动等要素投入）增长解释的残差，为“广义上的技术进步”。

　　广义上的技术进步包括：引起生产函数移动的狭义技术进步、规模经济、更有效的资源配置、更好的投入品质量等

　　上图为丹尼森（Edward Dension）对 5 个发达国家的全要素生产率的分解结果。在测算全要素生产率时，使用上面推导的人均产出的增长核算方程：\(g_{ (Y/N) } =g_A+\alpha g_{ (L/N) } + \beta g_{ (K/N) }\)，其中国家的人口数量 \(N\) 被替换为了雇员数量。在分析每个雇员实际收入增长时，使用的是人口数量而非雇员数量。

　　第 7 行的单位常规性投入的产出，由第 3 行与第 4 行相减得到，即每个雇员的收入和常规性总投入的差（因为取了对数，商运算转化为差运算）。发达国家的全要素生产率对收入增长起到决定性作用，贡献份额大约为 70%~100%。

　　将第 7 行的全要素生产率分解为：

• 第 8 行：年龄性别构成
• 第 9 行：教育，假定工资率差异的 \(3/5\) 是由正规教育的差异造成的
• 第 10 行：资源配置改进，包括从生产率较低的部门转移到生产率较高的不么的劳动力再配置（使用自我雇佣流向其他职业后工人报酬增加总量衡量）、贸易自由化引起的赚取收入能力改进（使用出口品价格上升或进口品价格下降引起的国民收入增量衡量）
• 第 11 行：规模经济
• 第 12 行：残差（技术进步），可以解释约 \(1/3 \to 1/2\)，即 8-11 项可以解释 \(1/2 \to 2/3\)

　　将第 13 行与第 6 行比较：教育和研究等无形资本投资对经济增长的贡献，要比有形资本积累的贡献大 1~2 倍。

　　处于工业化初期的发展中国家过渡到发达国家的基本条件是：增加教育和研究方面基础设施的投资。

3.2 学校教育和经济增长

　　学校教育具有高回报率。由于知识和信息具有公共品属性，通过学校教育积累的人力资本而开发的知识大多都被外部化了，因此不能简单将学校教育的私人回报（受教育者的赚钱能力）算作教育收益。

　　学生将学校里获得的知识转化为生产和管理方面有用的技能通常需要较长时间。而学生在高等教育机构中学习到能创造有用的知识、或者做出能被广泛应用于实际生产过程的发明/科学发现，可能需要更长的时间。

　　因此，对于贫穷国家而言，教育投资的短期回报非常低，

　　两个假设：

• 物质资本和人力资本之间可能具有互补性。除非有平行增长的人力资本提供支持，否则物质资本的积累必将面临回报大幅下降；除非物质资本和人力资本恰当地结合，否则通过教育获得的技能和知识对生产率增长的贡献十分有（卢卡斯 - Robert Lucas, 1988）。
• 影响一个国家引进外来技术的能力，进而影响经济增长率的主要决定因素，是教育水平而非教育增长率。（Robert J. Barro & Gregory Mankiw）

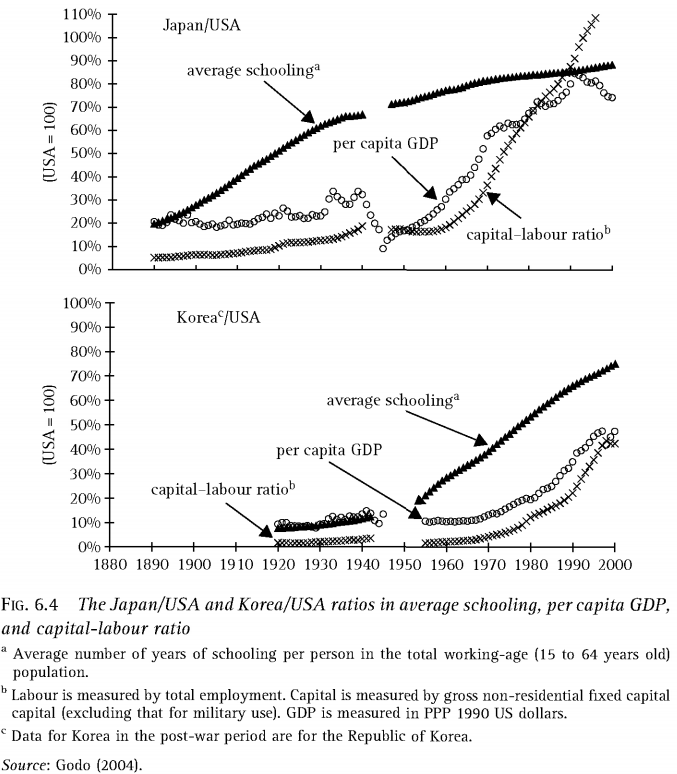
　　日本的案例：

• 在第二次世界大战以前（特别是 1930 年以前），日本的教育投已经快速积累，但通过学校教育创造的人力资源尚未达到可以有效引进美国应用的前沿技术的门槛，因此教育的直接经济收益并不高。
• 在 1950 年以后，日本的教育投资积累已经使其迈过了技术引进的门槛，可以充分利用前沿技术推动经济发展。

　　朝鲜半岛的案例：

• 1910 年，朝鲜半岛被日本占领成为殖民地，日本建立了初等教育体系，但没有发展更高水平的教育，教育对经济增长的影响很小；
• 1948 年，朝鲜半岛独立后，为发展教育事业投入来了大量的资金和努力，和发达国家（美国）的教育差距迅速减小，在前 20 年，教育对经济增长的作用还较小；在 20 世纪 70 年代，由于人力资本积累达到了充分利用引进技术的门槛，因此教育对经济增长的作用越来越大。

　　对于二战后新独立的发展中国家，种族往往构成复杂，宗教信仰、种族等冲突较大，教育是构建民族认同和国家认同的有利工具。使用同一种语言教授统一课程的的学校，尤其是小学教育，是培养民族认同和促进不同族群在民族利益上达成共识的最有效途径。

补充：

中国的教育对工业化的促进作用

中国目前的高等教育与社会生产脱节的问题

3.3 回报递增和内生增长模型

　　丹尼森的增长核算，知识简单区分了劳动、资本的贡献，并将其他贡献全部归入残差种，不能解释规模经济产生的原因，也不能解释人类知识如何改进、知识如何积累与如何阻止经济规模报酬递减。罗默（Paul Romer, 1981）和卢卡斯（Robert Lucas, 1988）提出“内生增长理论”，将上面的机制包含在内。

　　索洛-旺斯模型基于新古典增长模型，认为技术进步是外生给定的。

　　内生增长模型假设：

• 知识积累来自公共部门的正式教育和私人部门的生产实践：用于提高经济生产的新知识是一点点积累而成的，除了通过公共部门对教育和科研的投资外，也通过私人企业在设计和构造更高效的机器和工厂时的投资活动。
• 知识创造具有公共物品属性：通过专利等手段保护企业所创造的有用知识，早晚也会地被其他企业所采用。

　　假设生产函数为劳动增进型（哈罗德中性）生产函数，技术进步仅提高劳动效率，而不影响资本效率。代表性企业 \(i\) 的生产函数为：

\[ \begin {align} Y_i = (EL_i ) ^{\alpha} K_i^{\beta} \end{align} \]

　　其中，\(Y_i\)、\(L_i\) 和 \(K_i\) 分别为特定企业的产出、劳动力和资本，\(E\) 为劳动力效率，\(EL_i\) 表示以效率单位衡量的劳动力投入。

　　假设所有公司生产活动所产生的知识影响该企业的劳动效率，而该企业生产活动产生的知识则不会影响。即：

\[ \begin {align} E= a K \end{align} \]

　　其中：\(a\) 为一个常数，决定决定经济体中总资本存量 \(K\) 和劳动平均效率 \(E\) 之间的平行关系。因此，将上式代入代表性企业 \(i\) 的生产函数：

\[ \begin {align} Y_i = [(aK) L_i ] ^{\alpha} K_i^{\beta} = a^{\alpha} K^{\alpha } \cdot L_i ^{\alpha} K_i^{\beta} \end{align} \]

　　定义：\(A=a ^{\alpha}\)，\(y_i = \frac {Y_i} {L_i}\)，\(k_i = \frac {K_i} {L_i}\)，上面两边同时除以劳动力数量 \(L_i\)，可得：

\[ \begin {align} y_i = A K ^{\alpha} k_i^{\beta} \end{align} \]

　　上面使用了 \(\alpha +\beta =1\)，原因是生产函数形式是哈罗德中性的。

　　由于 \(k= K/L\)，因此上式可以改写为：

\[ \begin {align} y_i = A L ^{\alpha} k ^{\alpha} k_i^{\beta} \end{align} \]

　　假设长期竞争性均衡，即所有公司的要素都实现同样的最优配置，即 \(k_i = k\)，\(y_i = y\)，因此，上式可以改写为：

\[ \begin {align} y= A L ^{\alpha} \cdot k \end{align} \]

　　在人口恒为常数的条件下，如果 \(AL\) 是一个常数，上式就等价于哈罗德-多马模型中的生产函数 \(Y=AK\)。对于恒定的人口，资本的边际生产率在整个 \(k\) 的范围内均为常数，\(k\) 和 \(y\) 呈现线性关系。如果人口增长，斜率将会更加陡峭，以至于 \(k\) 和 \(y\) 的增长率上升。因此，上面的函数可以被改写为：

\[ \begin {align} \frac Y K= A L ^{\alpha} \end{align} \]

　　这说明，人口增长将导致资本产出比率 \(K/Y\) 的下降，人口增长有可能提高资本效率。

　　内生增长模型和亚当·斯密观点的相同之处：资本积累促进劳动分工，进而促进经济效率的提高。

3.4 熊彼特和中央计划经济

　　依靠资本积累（有形资本和无形资本）实现经济增长有一个前提：有形资本和无形资本要具有充分的互补性。

　　教育和研究投入是马克思增长类型向库兹涅茨增长类型转变的必要条件，而非充分条件。像前苏联这样的中央计划经济的中小学普及率远高于资本主义市场经济的普及率，高等教育和研究体系方面的公共投入也很高（约占 GDP 的 4%），明显高于发达资本主义市场经济国家的 2%~3%。但是，中央计划经济不能实现持续的经济增长。

3..4.1 熊彼特的创新理论

　　（网页链接）

　　与古典学派、马克思等观点（资本积累拉动资本主义经济发展）不同，熊比特的观点：

• 创新是资本主义经济发展的动力；

• 创新不是科学发现和发明，而是企业家利用新思想创造出新的生产要素组合来增加利润的过程；

• 创新的形式：

  • 引进一种新产品或具有新特性的产品：引进晶体管代替真空管
  • 引进新的生产方法：开发低成本大批量的晶体管生产体系
  • 开发新市场：开拓晶体管的海外市场
  • 获得原材料供给的新渠道：利用硅晶体这种新材料
  • 采用新的产业组织：组织开发工业园区和投机资本市场

　　在没有创新的情况下，市场竞争最终将使所有经济部门失去超额利润，经济将进入收入等于成本（市场价 \(P\) 为长期平均成本曲线 \(LAC\) 的最低点）的长期均衡的停滞状态。（传送门：竞争厂商的长期供给曲线）

　　持续不断地创新是资本主义的基本特征，因为追逐利润的企业家总是试图根据需求和生产可能性的变化，引进新产品和新生产方法来增加利润。如果这种持续不断的创新机制停止了，就不再是资本主义经济，而是非资本主义经济。

　　从事创新的企业家是为了追逐超额利润而承担风险的经济人。率先实现创新的企业家往往能获得大量的超额利润，但也面临创新带来的风险，例如新产品销量低或者新机器生产效率低于预期。

　　企业家可以通过向银行贷款获得创新所需的雇佣工人或购买设备等的资本金，资本家和企业家的身份有可能会分离。创造银行信贷的过程（资本从银行流向企业家）会导致市场价格上升，一般公民的实际收入和消费下降，创造银行信贷的过程造成了被迫储蓄，资本从消费者流向企业家以形成创新投资。因此，经济发展的主要动力是创新，资本积累过程则是动员创新所需的储蓄的过程。

　　当创新成功成功时，其他企业家会模仿这种生产行为，新商品的供给会扩大，使得其市场价格逐渐降低；生产要素的需求增加，会使要素价格上升。产品价格下降和要素价格上升的双重作用下，超额利润将逐渐下降，直到市场价格等于长期平均成本曲线最低点时达到新的均衡。

　　参与创新的企业家，被胡萝卜（超额利润）所吸引，也被鞭子（市场竞争）所驱赶。

3.4.2 中央计划经济的问题

　　中央计划经济通过资本积累难以实现经济增长的可能原因，是缺乏能够调动企业家为满足社会需求的创新而努力的市场机制。

　　在中央计划经济中，提高工作努力程度的主要目的是完成产出的数量目标，产品质量改进相对被忽略。市场经济中私有企业的产品质量降低会失去顾客，但在国家收购和分配体制下，国有企业不会受到惩罚。工人的工资与福利待遇很难降低，缺乏生产工艺的改进导致生产要素的浪费。中央计划经济的低效率还体现在依赖行政体制和人际关系，行贿和恐吓行为无法避免。

　　由于缺乏利润激励和市场竞争，中央计划经济会导致生产要素使用效率下降，全要素生产率对经济增长的贡献降低。

　　要通过资本积累（无形资本和有形资本）实现经济增长，需要破除中央计划经济的弊端，发展竞争性的市场机制，让作为创新主体的企业家被超额利润吸引（胡萝卜），同时被市场竞争驱赶（鞭子）。

　　同时，竞争性市场的有效运行需要完善法律制度和政策，例如产权保护制度、合同实施制度、治安和司法制度。

3.5 引进技术的制度条件

　　发展中国家的技术进步主要源泉是从发达工业国引进先进技术。

　　发展中国家具有后发优势，因为引进发达国家技术可以提高工业的增长率，但不用承担技术创新过程的风险和损失。

　　在工业化初期，银行制度很重要（格申克隆，Gerschenkron, 1962）。在初始阶段，国内企业家积累的资本很少，从国外引进资本密集度高的先进技术需要很大的资本。建立银行体系可以实现大范围的公民储蓄，以实现工业资本积累。