本文关注工具变量法，从工具变量的原理和选择，着重讨论怎么使用工具变量法、怎么检验工具变量的有效性。在文章的第五章，讨论了工具变量估计的外部有效性，该部分内容来自连享会。

一、工具变量法原理

1. 因果推断中的工具变量法

在因果推断中，为得到干预行为的净效应，干预行为 \(D_i\) 需满足条件独立性假设（Conditional Independence Assumption, CIA）：

\[ \begin{align} (Y_{0i},Y_{1i}) \perp D_i \ | \ X_i \end{align} \]

在满足条件独立性假设的前提下，使用 OLS 回归或者 PSM 都可以得到干预行为的净效应，即 ATT 或 ATE 。然而在现实中，受制于数据的可得性，遗漏变量问题无法避免，OLS 法和 PSM 估计难以满足 CIA 假设，通过添加变量来控制差异的做法可能无法得到真实的干预行为净效应。

例如在探究教育年限 \(D\) 对收入 \(Y\) 的影响时，学生的能力 \(A\) 可能是一种混杂因素，即学生的能力越强，其接受教育的年限可能越高，同时收入也可能会越大。传统 PSM 法估计无法解决学生能力等内部混杂因素与政策环境等外部混杂因素对因果识别结果的扭曲，这也是工具变量法区别于 PSM 的关键。

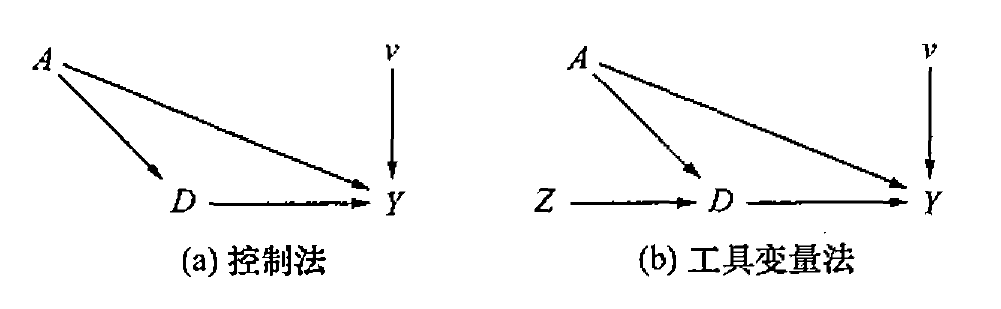
工具变量法的有相无环图

在工具变量法 (右图 b) 中，如有向无环图所示，如果存在一个工具变量 \(Z\) 满足相关性与外生性的条件，就可以消除混杂因素 \(A\) 对结果的扭曲。

工具变量的三个假设：

  • 相关性：\(Cov(D_i, Z_i) \ne 0\)，即工具变量 \(Z\) 与干预变量 \(D\) 相关
  • 外生性：\(Cov(\eta_i, Z_i) = 0\)，即工具变量与 \(Z\) 与包含混杂因素 \(A\) 的残差项 \(\eta\) 不相关，其中 \(\eta_i = A^{'}_i \gamma +v_i\)。( 工具变量的外部有效性 )
  • 排他性： 工具变量 \(Z_i\) 仅能通过干预变量 \(D_i\) 影响 \(Y_i\)​

（工具变量的假设其实只包含“相关性”和“外生性”，但是在实际检验过程中，由于外生性比较难直接检验，一些研究采取排除其他影响路径可能性的做法，用于检验“外生性”。“外生性”与“排他性”实质是相同的，但是在实际研究中，讨论和检验“外生性”的步骤往往更加简单，使用排他流程往往更加复杂。）

工具变量可以消除混杂因素影响的原理是：

阻断后门路径 \(D \leftarrow A \rightarrow Y\)，从其中分离出 \(D \rightarrow Y\)。

在实证中，为保证因果效应被准确识别，如果存在 \(m\) 个混杂因素，应当需要不少于 \(m\) 个工具变量。

2. 非因果推断中的工具变量法

在因果推断中，常将干预变量 \(D_i\) 设定为一个 0-1 变量，然而，干预变量为连续变量或多分类变量的情况更为常见。在连续变量和多分类变量的条件下，满足工具变量的三个假设，同样也可以用于模型中排除遗漏变量导致的估计偏误。

二、常用的工具变量

查看前的强烈推荐：​超过 1600 篇外文顶刊文章的工具变量汇总，还在动态更新!

工具变量选择方法

来源：《IV 的标准动作：工具变量法实用指南》，连享会

本节参考资料：计量经济圈推文

1. 截面数据中常用的工具变量

1.1 自然或地理特征

由于经济系统的内生性很强，在许多研究中，为了规避内生性问题，会选择找看起来“严格外生”、不受经济系统干预和人类行为影响的变量作为工具变量。例如，天气、降水、温度（积温）、自然灾害、地形地貌、地理距离。

这类工具变量又可以分为两类：

  • 人类完全无法控制其变化的自然因素：天气、降水、温度（积温）、自然灾害等。这类工具变量受到质疑其外生性的可能性较小，但往往会受到研究主题限制，适用范围较小，需要严格根据选题来确定。

  • 客观存在且很难改变的特征：地形地貌、地理距离（地理距离、驾车距离）等。

    • 高程： 常用于研究基础设施建设、交通等内生变量的影响，认为高程不会（直接）影响经济发展等。然而城市扩张、经济发展往往优先在平原地区进行。高程并非严格外生。
    • 距离河流、山脉等自然地貌的地理距离： 与高程类似，地理距离往往不会直接影响经济系统，但是经济系统的构建往往依赖于自然地貌。看似地理距离也非严格外省。（例如：《科举万岁》的文章中，用到竹子产地的距离作为工具变量。）
    • 距离行政中心、经济中心的地理/驾车距离： 更加常用，与自然地貌相比，由于其目的地是行政中心、经济中心，这种影响路径更加复杂，距离本身可能也是影响结果变量的重要因素。

虽然这么说，但是还是值得计算到行政中心/经济中心的距离。可以使用高德地图或百度地图的开发者账号，通过指定的函数计算出需要的内容。

  • 获取开发者账号权限，获得秘钥
  • 使用软件输入格式化的函数（教程链接），在函数对应位置填写秘钥
  • 根据出发地和目的地的地址名称，调用地图平台的 api，计算出出发地和目的地的经纬度
  • 基于两个经纬度，自动计算导航距离/时间。

1.2 关联特征

1.2.1 与内生变量关联

案例 1：与制度相关的教会（文化影响）​知网链接

方颖和赵扬(2011)在各地产权保护制度对经济增长影响的研究中，将 1919 年中国不同城市基督教初级教会小学注册人数占当地人口比例作为工具变量，主要原因是，该比例可在一定程度上代表在历史上该地区受西方影响的程度，入读教会小学的比例越高，表明该地区受西方影响越大，建立产权保护制度的意识较强，而建立教会小学的初衷是布道，与经济发展水平并不直接相关。

案例 2：与历史相关的基础设施（地理位置）​知网链接

谭伟杰等（2024）在政府数字采购政策对企业商业信用融资能力的影响的研究中，使用明朝驿站和时间趋势项的交互项作为工具变量。原因是驿站往往建在古代信息条件好、通讯基础设施更加完善的地区，驿站数量与当代的数字经济有正向关联；但是，古代驿站建设主要出于军事考虑，与企业的商业信用关联较小。

1.2.2 与受访个体关联

家庭内关联： 子女的教育程度与父母的挂钩，用父母的教育教育程度作为工具变量；用双胞胎另一个孩子的情况作为工具变量。

区域内关联： 邻居的情况，邻居是否加入合作社，会影响受访者的加入意愿。

1.3 同侪效应

同侪效应是一种特殊额度关联个体的指标。

同侪效应 / 同伴效应 / 伙伴效应： 同一组内其他样本的行为或状态可能会影响受访者的行为与状态。

同侪效应常用作工具变量，原因是：本组内其他样本的行为和状态会对受访者产生影响，但是并不会直接影响受访者的结果变量 \(y_i\)。

假设某一组内共有 \(m\) 个样本，对于受访者 \(i\)​，其同侪效应 $X_p $ (组内其他样本均值) 可以表示为：

\[ \begin {align} X_p= \frac {\sum _{j \ne i} X_j} {m-1} = \frac {\sum _{j =1}^n X_j \ - \ X_i} {m-1} \end{align} \]

计算步骤包括：

  • 计算组内样本数量 \(m\)；
  • 计算组内所有样本变量 \(X\) 的取值之和；
  • 代入上式计算同侪效应 \(X_p\)。

因此，可以按如下过程计算：

1
2
3
4
** 使用 count 和 total 函数:
egen count_num=count(X), by(CID)    // 分组计算变量 X 的非缺失值样本数量
egen X_total=total(X), by(CID)      // 对 X 的分组求和
gen X_p=(X_total-X)/(count_num-1)

上述计算过程比较麻烦，也有学者开发了 peers​ 函数，可以等效替代上面的命令：

1
2
3
** 使用 peers 函数: 以 CID 分组, 组内其他受访者的 X 均值
ssc install _peers, repalce       //安装 peers 函数，仅首次使用需要安装
egen X_peers=peers(X), by(CID)             //CID 为分组变量, 包含 X 为缺失值的样本

peers​ 函数对存在缺失值的情况应对并不好，因此需要做一点小处理。即确保分组的 CID​ 和待计算的 X​ 不能是缺失值：

1
egen X_peers=peers(X) if X!=. & CID!=., by(CID)

2. 面板数据中常用的工具变量

2.1 时变变量作工具变量

自然因素、地理特征或外部冲击：

《农业比较优势与立法者对贸易协定的支持》农业比较优势对贸易协定的影响，天气与土壤因素作为工具变量，属于外生自然因素。

《警察知道该拦截谁吗？》美国警察拦截车辆或者行人，检验检查点数量对犯罪率的影响，工具变量是 COVID-19 和 George Floyd 遇害后全国抗议活动，这两个外生的事件爆发导致了检查点增加，但并没有降低犯罪率。

内生变量的滞后项：

《超越大火：森林火灾对能源贫困的影响》滞后的森林火灾作为工具变量。

2.2 非时变变量作工具变量

非时变变量往往无法直接作为工具变量，常见做法是和时变变量作交互项，构成时变的工具变量。

做法一：非时变变量与时间趋势的交互项

谭伟杰等（2024）在政府数字采购政策对企业商业信用融资能力的影响的研究中，使用明朝驿站和时间趋势项的交互项作为工具变量。原因是驿站往往建在古代信息条件好、通讯基础设施更加完善的地区，驿站数量与当代的数字经济有正向关联；但是，古代驿站建设主要出于军事考虑，与企业的商业信用关联较小。

做法二：非时变变量与时变变量的交互项

任劼（2024）探究营商环境对城乡收入差距的影响，参考Nunn & Qian（2014）的做法，引入一个随时间变 化的变量——当地普通高等学校人数的滞后一期，与 2007 年财产保险的赔付支出相乘构造交互项 组成面板数据，形成营商环境的最终工具变量。

三、常用的工具变量法

1. 基于两步估计的工具变量法

1.1 最为常见的两阶段估计：两阶段最小二乘法（2SLS）

\[ \begin{align} x_i &= \gamma z_i + \lambda w_i + \xi_i \\ y_i &= \beta \hat x_i + \delta w_i + \mu_i \end{align} \]

2SLS 的本质是将第一阶段计算出的工具变量 \(z_i\) 对内生变量 \(x_i\) 的拟合值 \(\hat x_i\)，代入第二阶段，用拟合值 \(\hat x_i\) 对 \(y_i\) 的估计系数进行替代。

1
2
3
4
5
6
** 最常见的2SLS
ivregress 2sls y $varlist1 (x = $ivlist), r
** 对弱工具变量更不敏感的LIML(有限信息最大似然法)
ivregress liml y $varlist1 (x = $ivlist), r
** 如果存在异方差, 用gmm估计比2sls更有效率
ivregress gmm y $varlist1 (x = $ivlist)

1.2 两阶段模型的修正与补充：2SPS 与 2SRI

推荐阅读： 赵娜,洪广彬.多项分布内生回归元计数模型的两阶段估计方法研究[J].统计与信息论坛,2018,33(08):19-30.

2SPS（Two-stage Predictor Substitution, 两阶段预测值替代估计）与 2SLS 类似，都是在第一阶段工具变量对内生变量进行估计，得到拟合值替代内生变量进行第二阶段估计（杨玉萍，2014）。但是随着计量经济学的发展和微观统计数据的完善，现代社会科学领域的经验性研究越来越多地开始使用非线性计量模型，如离散选择模型、计数模型和受限因变量模型等。当内生变量为服从某一特定分布的离散型变量时，忽略内生变量的特殊性质而仍然采用 2SLS 法，就会导致非一致的参数估计量（赵娜、洪广彬，2018）。

1.3 两阶段残差包含法（Twostage Residual Inclusion, 2SRI）

\[ \begin{align} x_i &= \gamma z_i + \lambda w_i + \xi_i \\ y_i &= \beta x_i + \delta w_i + \hat R_i + \mu_i \end{align} \]

2SRI 本质是将第一阶段得到的估计残差 \(\hat R_i\) 代入第二阶段，以消除内生性影响。

注意事项：

  • 2SRI 模型没有集成的命令包，需要手动调整变量和参数。
  • 2SRI 模型涉及矩阵运算，在使用前需要确保模型使用到的所有变量（\(y_i\)、\(x_i\)、\(z_i\) 和控制变量 \(w_i\)）均没有缺失值。
  • 2SRI 的第一阶段估计和第二阶段估计的控制变量需要完全相同，否则无法进行矩阵运算。

模型优点：

  • 可以通过第一阶段估计模型的设定，针对内生变量不同分布选择 2SRI 类型
  • 当模型存在忽略模型非线性、内生性或错误设定计数数据分布时，2SLS 和 2SPS 会存在较大的估计偏差，但 2SRI 具有良好的有限样本特性（赵娜、洪广彬，2018）

2SRI 的用法可以参考下面的文章：

  1. Terza J V. Simpler standard errors for two-stage optimization estimators[J]. The Stata Journal, 2016, 16(2): 368-385.
  2. Terza J V. Two-stage residual inclusion estimation: A practitioners guide to Stata implementation[J]. The Stata Journal, 2017, 17(4): 916-938.

2. 内生转换模型 ESR

在截面数据中，当内生变量 \(x_i\) 为二分类变量时，例如“是否加入合作社”，可以使用内生转换模型处理内生性问题。根据结果变量 \(y_i\) 的类型不同，应当使用不同的内生转换模型。

  • \(y_i\) 为二分变量，使用内生转换概率模型（ESP），使用 switch_probit 命令即可实现
  • \(y_i\) 为连续变量，使用内生转换回归模型（ESR），使用 movestay 命令即可实现

拓展链接：

3. 拓展回归模型 ERM

需要明确的是：拓展回归模型 ERM 是一类模型，不是一个具体的模型。

拓展回归模型“拓展”了什么？

  • 拓展的模型种类： 相对 regress​、probit​ 、oprobit​、logit​、tobit​、intreg​ 等基础模型的内生性拓展
  • 拓展内生性： 与常用的解决内生性的模型可以得到相同的估计结果，但在多内生变量、工具变量等情形下，可以设置不同的工具变量和控制变量，得到不同的估计结果
  • 拓展样本选择： 解决样本选择问题
  • 拓展处理效应： 添加处理效应模块，可以计算非随机条件下的处理效应
  • 检验值： 自动汇报比常规模型更多的检验值

以 reg ​的拓展 eregress ​为例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
** 内生协变量 (Basic linear regression with endogenous covariates)
eregress y [indepvars], endogenous(depvars_en = varlist_en)   // _en后缀为内生变量, indepvars 与varlist_en可以相同, 也可以不同

** 内生处理效应 (Basic linear regression with endogenous treatment assignment)
eregress y [indepvars], entreat(depvar_tr [= varlist_tr])    // _tr 后缀为内生处理变量

** 外生处理效应 (Basic linear regression with exogenous treatment assignment)
eregress y [indepvars], extreat(tvar)                      // tvar 处理变量

** 样本选择问题 (Basic linear regression with sample selection)
eregress y [indepvars], select(depvar_s = varlist_s)       // _s 后缀为样本选择变量

** 内生协变量 + 处理效应 + 样本选择
eregress y [indepvars] [, extensions options]

以 xtreg ​的扩展 xtregress ​为例：

1
2
3
4
5
** 随机效应模型 (Basic linear regression with random effects)
xteregress y [indepvars] [, options]

** 随机效应 + 内生协变量 + 处理效应 + 样本选择
xteregress y [indepvars] [, extensions options]

4. 其他工具变量法

放松假设、对原有扩展模型扩展：

工具变量方法在其他模型、数据的应用：

四、工具变量的检验

1. 常见检验项目：四大项目

豪斯曼检验（Hausman test）： 检验解释变量内生性，需要同方差假设，因此不能使用稳健标准误

1
2
3
4
5
qui reg y x $varlist1
est store ols 
qui ivregress 2sls y $varlist1 (x = $ivlist)
est store iv 
hausman iv ols, constant sigmamore

不可识别检验（Underidentification test）： 使用工具变量法的前提之一是秩条件成立，即 \(L\) 个工具变量的秩为 \(z_i\)，\(K\) 个内生变量（解释变量）的秩为 \(x_i\)，那么要求 \(z_i\) 与 \(x_i\) 有重叠元素，且 \(L >= K\)。对于不满足列满秩的情况，可以使用 ivreg2​ 命令进行检验，可以查看 Kleibergen-Parp rk LM 统计量。

弱工具变量检验（Weak instruments test）： 如果内生变量与工具变量的仅微弱相关，工具变量中与内生变量相关的信息很少，就会存在弱工具变量问题，可以使用四种方法判别：

  • 方法一：偏 R2（Shea's partial R2），Shea（1997）提出
  • 方法二：最小特征值统计量（minimum eigenvalue statistics），Stock and Yogo（2005）提出。在只有一个内生解释变量的条件下，该统计量还原为 F 统计量
  • 方法三：假设扰动项独立同分布（iid），使用 Cragg-Donald Wald F 统计量（Cragg and Donald，2005），临界值由 Stock and Yogo（2005）提供
  • 方法四：如果扰动项不满足 iid 假设，使用 Kleibergen-Paap Wald rk F 统计量，临界值来自 Stock and Yogo（2005）
  • 其他检验方法：弱工具变量检验：twostepweakiv​，使用两步法检验线性工具变量估计中工具变量的稳健性

过度识别检验（Overidentification test）： 工具变量比内生变量多，则需要做过度识别检验。原假设：“H​0：所有工具变量都是外生的”。

1.1 命令：

1
2
3
4
5
6
7
** 在ivregress 2SLS下的弱工具变量检验
ivregress 2sls y $varlist1 (x = $ivlist), r
estat firststage, all forcenonrobust
estat overid

** 在ivreg2下的弱工具变量检验
ivreg2 y $varlist1 (x = $ivlist), r

1.2 ​ivregress 2SLS​​ 下的工具变量检验示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
** 案例数据: download from here: https://fgzfgz.github.io/posts/16796/
use grilic, clear
ivregress 2sls lw s expr tenure rns smsa (iq = med kww mrt age), r

** 1. 弱工具变量
estat firststage, all forcenonrobust
/*  First-stage regression summary statistics
  --------------------------------------------------------------------------
               |            Adjusted      Partial       Robust
      Variable |   R-sq.       R-sq.        R-sq.      F(4,748)   Prob > F
  -------------+------------------------------------------------------------
            iq |  0.3175      0.3093       0.0533       9.58518    0.0000
  --------------------------------------------------------------------------

  Shea's partial R-squared     // 弱工具变量方法一
  --------------------------------------------------
               |     Shea's             Shea's
      Variable |  partial R-sq.   adj. partial R-sq.
  -------------+------------------------------------
            iq |     0.0533             0.0432
  --------------------------------------------------

  Minimum eigenvalue statistic = 10.5383    // 弱工具变量方法二  
  Critical Values                      # of endogenous regressors:    1
  H0: Instruments are weak             # of excluded instruments:     4
  ---------------------------------------------------------------------
                                     |    5%     10%     20%     30%
  2SLS relative bias                 |  16.85   10.27    6.71    5.34
  -----------------------------------+---------------------------------
                                     |   10%     15%     20%     25%
  2SLS size of nominal 5% Wald test  |  24.58   13.96   10.26    8.31
  LIML size of nominal 5% Wald test  |   5.44    3.87    3.30    2.98
  ---------------------------------------------------------------------   */

** 2. 过度识别检验
estat overid
/* Test of overidentifying restrictions:
  Score chi2(3)          =  51.5449  (p = 0.0000)  */

1.3 ​ivreg2​​ 下的工具变量检验示例：

使用 ivreg2​ 可以直接汇报更多的检验结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
** 案例数据: download from here: https://fgzfgz.github.io/posts/16796/
use grilic, clear
ivreg2 lw s expr tenure rns smsa (iq = med kww mrt age), r

** 1. 弱工具变量检验
/* Estimates efficient for homoskedasticity only
Statistics robust to heteroskedasticity

                                                      Number of obs =      758
                                                      F(  6,   751) =    58.74
                                                      Prob > F      =   0.0000
Total (centered) SS     =  139.2861498                Centered R2   =   0.2002
Total (uncentered) SS   =  24652.24662                Uncentered R2 =   0.9955
Residual SS             =    111.39959                Root MSE      =    .3834

------------------------------------------------------------------------------
             |               Robust
          lw | Coefficient  std. err.      z    P>|z|     [95% conf. interval]
-------------+----------------------------------------------------------------
          iq |  -.0115468   .0056376    -2.05   0.041    -.0225962   -.0004974
           s |   .1373477   .0174989     7.85   0.000     .1030506    .1716449
        expr |   .0338041   .0074844     4.52   0.000      .019135    .0484732
      tenure |    .040564   .0095848     4.23   0.000     .0217781      .05935
         rns |  -.1176984   .0359582    -3.27   0.001    -.1881751   -.0472216
        smsa |    .149983   .0322276     4.65   0.000     .0868182    .2131479
       _cons |   4.837875   .3799432    12.73   0.000       4.0932     5.58255
------------------------------------------------------------------------------
Underidentification test (Kleibergen-Paap rk LM statistic):             33.294    // 不可识别检验
                                                   Chi-sq(4) P-val =    0.0000
------------------------------------------------------------------------------
Weak identification test (Cragg-Donald Wald F statistic):               10.538    // 弱工具变量方法三
                         (Kleibergen-Paap rk Wald F statistic):          9.585    // 弱工具变量方法四
Stock-Yogo weak ID test critical values:  5% maximal IV relative bias    16.85
                                         10% maximal IV relative bias    10.27
                                         20% maximal IV relative bias     6.71
                                         30% maximal IV relative bias     5.34
                                         10% maximal IV size             24.58
                                         15% maximal IV size             13.96
                                         20% maximal IV size             10.26
                                         25% maximal IV size              8.31
Source: Stock-Yogo (2005).  Reproduced by permission.
NB: Critical values are for Cragg-Donald F statistic and i.i.d. errors.
------------------------------------------------------------------------------
Hansen J statistic (overidentification test of all instruments):        51.545    // 过度识别检验
                                                   Chi-sq(3) P-val =    0.0000
------------------------------------------------------------------------------
Instrumented:         iq
Included instruments: s expr tenure rns smsa
Excluded instruments: med kww mrt age
------------------------------------------------------------------------------   */

2.工具变量的假设检验

2.1 截面数据的工具变量假设检验

2.1.1 相关性的假设检验

含义：内生变量 \(x\) 与工具变量 \(z\) 之间有关联，而且非弱关联。

  • 使用弱工具变量检验结果论证内生变量 \(x\) 与工具变量 \(z\) 之间的关系不是弱关联
  • 回归法：构建 \(z\) 对 \(x\) 的简单 OLS 回归，例如：reg x z​
  • 第一阶段回归结果：两步估计（2SLS、2SPS、2SRI）第一阶段工具变量 \(z\) 对内生变量 \(x\) 显著性
2.1.2 外生性的假设检验

含义：结果变量 \(y\) 与工具变量 \(z\) 之间无关联，或者说无直接关联。

  • 无关联情况：reg y z​，\(z\) 不显著
  • 无直接关联情况：reg y z​，\(z\) 显著；reg y x z​，\(z\) 不显著。说明 \(z\) 的显著性来仅自于 \(x\)。（Link）

第二种“无直接关联情况”，需要注意的是，​reg y x z​​ ，​\(z\) 不显著，是外生性假设成立的充分非必要条件​ ！ （赵西亮，2017，《基本有用的计量经济学》）

  • 充分：​reg y x z​，\(z\) 不显著，说明 \(z\) 的显著性来仅自于 \(x\)，外生性成立。
  • 非必要：​reg y x z​，\(z\) 显著，不能说明 \(z\) 不满足外生性。
2.1.3 排他性的假设检验

在传统的因果推断相关教材中，并不包含排他性的这一假设。排他性假设本质是外生性假设的外延。

当工具变量满足外生性的充分条件（“无直接关联”情况）时，一般情况下无需进行排他性检验。然而，外生性的充分条件尝尝难以满足。通过排他性来论证工具变量 \(z\) 对结果变量 \(y\) 的影响仅来自内生变量 \(x\)，就是一种可选的做法。

  • 排除其他影响路径的做法：经典文献​
  • 控制函数法下的排他性检验：testex​，链接

2.2 面板数据的工具变量假设检验

滞后项做工具变量的前提（链接）：

  • 不可观测因素不存在序列相关：\(U_{t-1} \nrightarrow U_t\)，无法检验
  • 内生变量是平稳的自回归过程：\(X_{t-1} \rightarrow X_t\)，可以检验

面板数据中滞后项做工具变量的有向无环图

2.3 常用工具变量的检验

同侪效应检验：​snreghnet​ 可以考察模型的行异质性和列异质性。snregenet​ 计算模型的两阶段工具变量估计，并采用野蛮自举计算标准误差。 (​2024 年 Stata 中国用户大会​ ，目前尚未发布)

3. 其他内生性与工具变量检验

3.1 遗漏变量检验

案例：吴刚,钟钰.地块规模与化肥投入：减施逻辑及其证据[J].华中农业大学学报,2024,43(03):27-38.

为考察可能存在的遗漏变量及其对回归的影响，可以使用 Oster (2019) 的提出的做法进行稳健性检验。当模型可能存在不可观测变量时，可以使用 \(β^*=β^* (R_{max},\delta)\) 获得真实系数的一致估计，其中 \(R_{max}\) 表示所有不可观测变量均能够被观测时回归方程的最大拟合优度；\(\delta\) 为选择比例，用于衡量相较于可观测变量和不可观测变量分别同核心解释变量之间相关关系的强弱，\(\delta=1\) 表示可观测变量与不可观测变量同等重要。参考 Oster (2019) 的参数设置，设定 \(R_{max} = 1.3R\)，即为当前回归方程拟合优度的 1.3 倍，然后采用以下两种方法进行检验：

  • 方法（1）：当 \(\delta=1\) 时，计算 \(β^* (R_{max},\delta)\)，若 \(β^*\) 落在了估计系数的 95% 置信区间内，则估计系数是稳健的；
  • 方法（2）：当 \(\beta =0\) 时，计算 \(\delta\) 的取值，若 \(\delta\) 的取值大于临界值 1，则通过检验。

检验结果如表 8 所示：

  • 当 \(R_{max} = 1.3R\)，\(\delta=1\) 时，估计系数 \(β^*\) 均落在 95% 置信区间内，由于置信区间不包括 0，且 \(β^*\) 的估计结果符号为负，方法（1）检验通过；
  • 当 \(R_{max} = 1.3R\)，\(\beta =0\) 时，此时，\(\delta > 1\)，方法（2）检验通过。

遗漏变量检验

3.2 近似外生工具变量检验

工具变量完全外生是一种理想状态，现实中估计模型仍然可能存在轻微的内生性问题。 由于工具变量的外生性难以检验，可以使用 Conley et al. (2012) 提出的近似零（local to zero, LTZ）和置信区间集合（union of confidence intervals, UCI），检验工具变量在近似外生的条件下估计结果是否具有稳健性。

使用 plausexog 命令（连享会链接），可以进行近似工具变量检验，包括置信区间方法（UCI）和近似零方法（LTZ）。

案例：**吴刚,钟钰.地块规模与化肥投入：减施逻辑及其证据[J].华中农业大学学报,2024,43(03):27-38.

LTZ 的结果表明，地块规模对化肥施用强度与化肥施用效率的影响在 1% 水平上显著为负；使用 UCI 估计工具变量近似外生条件下置信区间，可以发现主回归的估计系数均落在 UCI 法计算出的置信区间内。 因此，当工具变量是近似外生时，估计结果仍然具有稳健性。

近似外生工具变量检验

五、工具变量估计中外部有效性的讨论

本节内容主要来自：连享会 - IV 估计中的外部有效性 (External Validity)

1. 什么是外部有效应？

1.1 含义

在政策评估中，对政策效应的估计大多集中在处理效应为常数，或者说平均处理效应 (ATE) 的情形。此时，隐含地假设了因果效应具有同质性，即所有个体处理效应都一样。然而，如果放宽这个假设，引入处理效应的异质性，那么就需要考虑一个问题：当类似于以下情况发生变化时，研究结论是否会改变？

  • 当有新个体加入实验，研究结论是否会改变？
  • A 州减税政策的评估结果，是否能直接用来指导 B 州的减税政策设计？
  • 如果不能直接使用，那么是否可以通过调整后使用？

1.2 案例

  • 研究一：利用随机抽取的参军资格作为工具变量 IV，来估计越战服役对收入的影响；
  • 研究二：估计志愿参军人员的参军经历对收入的影响。

研究一的估计结果不能用在研究二中。 这是由于两个样本中个体并不相同，即研究一中更接近随机，而研究二中那些志愿参军的人员，可能本身就是收入偏低的劳动人群。

2. 局部平均处理效应 (LATE)

在 IV 分析框架中，我们尝试通过引入工具变脸来创造因果链条：通过工具变量 Z 影响我们感兴趣的变量 \(D\)，然后 \(D\) 再去影响潜在结果 \(Y\)。

需要注意的是，不论干预变量 \(D_i\) 是何种类型，工具变量法的结果都不可作为因果效应（ATE），仅可将结果解释为局部平均处理效应（Local Average Treatment Effect，LATE）。

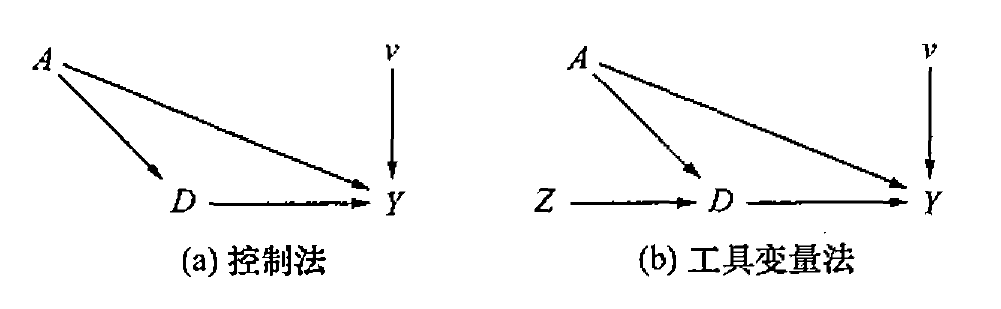
[工具变量法的有相无环图](assets/net-img-image-20221018182903-oq4blvn-20221021221423-dp6aln3.png" style="width:550px" alt="工具变量法的有相无环图" />

在参军的例子中，工具变量 \(Z\) 为随机抽取的参军资格，干预变量 \(D\) 为是否参军，那么根据是否有参军资格、是否参军，可以将人群划分为四大类：

  • 如果有参军资格（\(Z=1\)），则参军（\(D=1\)）；
  • 如果没有参军资格（\(Z=0\)），则不参军（\(D=0\)）；
  • 如果没有参军资格（\(Z=0\)），也会参军（\(D=1\)）；
  • 如果有参军资格（\(Z=1\)），也不参军（\(D=0\)）。

工具变量估计到底是对什么群人的估计？

  • IV 估计可以解释的两类人群（依从工具变量者，compliers）：

    • 如果有参军资格 (\(Z=1\))，则参军 (\(D=1\) )；
    • 如果没有参军资格 (\(Z=0\))，则不参军 (\(D=0\))。

  • IV 估计不能解释的两类人均：

    • 始终接受者（always-takers）： 不论是否有参军资格（\(Z=0 \ \ or \ \ Z=1\)），都要参军（\(D=1\)）；
    • 始终不接受者（never-takers）： 不论是否有参军资格（\(Z=0 \ \ or \ \ Z=1\)），都不参军（\(D=0\)）。

当依从工具变量者（compliers）只占实验人群一部分时：

  • IV 估计出来平均因果效应往往不等于所有 \(D=1\) 的人的平均处理效应；
  • IV 估计出来的未受处理的个体的平均处理效应也不等于所有 \(D=0\) 的人的平均处理效应。

3. LATE 的外部有效性

当随机实验中不只是 compliers 人群时，如何在工具变量局部因果框架下，去估计所有实验组个体的平均因果效应呢？或者说，如何评估该实验中 LATE 的外部有效性呢？

利用异质性因果效应和边际处理效应 (MTE) 可以识别 IV 估计下的内部效度和外部效度（外部有效性）问题。

3.1 边际处理效应

Kowalski 编写了 mtebinary​ 和 mtemore ​命令，用于估计二元工具变量下的边际处理效应。

[1] Kowalski A, Tran Y, Ristovska L. MTEBINARY: Stata module to compute Marginal Treatment Effects (MTE) With a Binary Instrument, Statistical Software Components, 2018.

[2] Kowalski A, Tran Y, Ristovska L. MTEMORE: Stata module to compute Marginal Treatment Effects (MTE) With a Binary Instrument, Statistical Software Components, 2018.

工具变量是一种思想： 工具变量的边际处理效应，是结合了二元变量的边际效应估计和工具变量解决内生性的思路。

3.2 删失数据的工具变量分位数回归

在内生性或外生性情况下，使用 cqiv ​命令，可以估计删失和未删失数据数据的估计。

工具变量是一种思想： 结合分位数回归和工具变量估计，可以在删失数据和未删失数据中考察异质性的因果效应估计。

文献来源：Chernozhukov V, Fernández-Val I, Han S, et al. Censored quantile instrumental-variable estimation with Stata[J]. The Stata Journal, 2019, 19(4): 768-781.

3.3 拓展材料：

3.4 为什么？普适性？

问题一： 为什么要考察 LATE 的外部有效性？

上面的很多回答都在尝试估计准确的二元政策干预效果。

  • LATE 的本质是忽略异质性影响得到的估计，主要关注估计结果的内部有效性；

  • LATE 的外部有效性，本质是关注异质性干预行为：

    • 干预行为的异质性：参军的例子中，考察随机抽取下受试群体的自选择行为，本质是其他未控制因素的异质性；
    • 结果的异质性：cqiv ​命令的例子中，考察（结果变量的）不同分位点处的异质性影响。

  • 结合机器学习的例子：张宏亮（2014, JDE）的例子，针对留守儿童随机干预的差异，结果“是否女孩儿”和“基线成绩”是影响干预行为效果的重要因素。

问题二： 为什么要针对二元干预变量考虑 LATE？在连续的干预行为里，没有普适性吗？

  • 在二元干预的估计里，将估计结果解释为因果效应已经尤为困难；在连续干预的估计里，估计结果更加难以解释为因果效应。

  • 二元干预估计的外部有效性讨论，对连续干预估计的最大启发是：

    • 需要关注工具变量和内生干预行为的相关性，工具变量包含内生变量的信息较少会导致弱工具变量问题，降低估计结果的可信度；
    • 连续干预估计中，工具变量既与内生干预变量相关、又与结果变量不直接相关非常困难。因此，多数工具变量往往不够外生，要关注工具变量的外生性检验。

外部有效性是回归方法的固有问题，难以完全回避。在解决外部有效性问题上，擅长预测的机器学习是否有更好的表现？

4. 外部有效性识别的 Stata 命令

4.1 针对二元工具变量的边际效应估计：mtebinary​ 命令

4.1.1 命令简介

mtebinary​ 命令安装如下：

1
ssc install mtebinary, replace

mtebinary ​的语法格式为：

1
mtebinary outcome  (endogvar = instrumen)  [covariates] [, options]

其中，

  • outcome​ 为结果变量，可以是二元、离散或者连续变量；
  • endogvar​ 为内生变量，必须是二元变量；
  • instrument​ 为工具变量，必须是二元变量；
  • covariates​ 为协变量。

opitions​ 主要包括两类：

  • 第一类为 Estimation​ 设置的选项，其中，

    • poly(#)​ 括号里填估计时回归函数的幂，默认为 1 次，即线性；
    • reps(#)​ 括号里填 bootstrap​ 的次数，默认为 200；
    • seed(#)​ 括号里填 bootstrap​ 的随机种子数，默认是 6574358；
    • bootsample(opt)​ 括号里填 bootstrap​ 的方式，可以是 strata(varlist)​，cluster(varlist)​，或者 weight​；
    • weightvar(varname)​ 括号里填需要赋予权重的变量名，默认没有赋予权重；

  • 第二类为 Post-Estimation​ 的相关选项，其中，

    • summarize(varlist)​ 括号里填协变量名称，输出这些协变量的三类人群的统计描述；
    • graphsave(graphsave)​ 括号里填输出图像的名称，默认名称为 mtegrapha。

4.1.2 命令用法示例

下面以没有协变量、MTE 效应为线性为例来展示命令的用法和结果。相关代码如下：

1
2
3
net get mtebinary       //下载数据 mtebinary_data.dta 到当前文件夹
use mtebinary_data.dta, clear
mtebinary Y2 (D = Z), reps (0) summarize (age female) graphsave (mte)

其中：

  • Y2​ 为急救室使用情况，D​ 为是否接受医疗服务，Z​ 为是否有资格医疗补助；
  • reps(0)​ 表示 bootstrap​ 次数为 0；
  • summarize(age female)​ 表示显示 compliers、always-takers 和 never-takers 这三类人群的 age​ 和 female​ 的统计性质；
  • graphsave (mte)​ 将图形结果保存名为 mte 的 pdf 文件。

主要回归结果为三个表和两个图，具体来看。

第一个表格为 "Average Characteristics of Always Takers, Compliers and Never Takers"，如下所示。其中第一列显示了所有人群的结果，第二列显示了 always-takers 人群的结果，第三列显示了 never-takers 人群的结果，第四列为 always-takers 人群和 compliers 人群的差异，第五列为 compliers 人群和 never-takers 人群的差异。从变量的统计结果，可以计算出 \(P_C=175/500=0.375\)，\(P_I=0.375+125/500=0.625\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Beginning Estimation of Marginal Treatment Effects (MTE) with a Binary Instrument.
MTE has been specified as a polynomial of order 1.
The number of bootstrap replication is 0
NOTE: $Y$ou have specified zero bootstrap replication. No standard error will be computed

Average Characteristics of Always Takers, Compliers and Never Takers
-------------------------------------------------------------------
           All     (1)       (2)      (3)    Differences  
                  Always  Compliers  Never     (1)-(2)    (2)-(3) 
                  Takers             Takers               
-------------------------------------------------------------------
 age      49.25   54.32    50.00     44.65      4.32       5.35   
 female    0.56    0.27     1.00      0.79      -0.73      0.21   
 Count   500.00  175.00   125.00    200.00               
-------------------------------------------------------------------

可以发现，不同类型人群间存在较为明显的统计差异。比如对于年龄而言，always-takers 人群年平均龄大于 compliers 人群 4.32 岁，约 8.6%；而 compliers 人群年龄平均大于 never-takers 人群 5.35 岁，约 10.67%。在这里，always-takers 人群最大，他们本身对医疗补助的需求也最大，而 never-takers 人群年龄最小，他们对医疗补助需求最小。

实际上，他们是否参与，部分可能是逆向选择的结果。可见，如果忽略不同类别间人群的显著差异，将 LATE 效应当成全部人群的平均处理效应，很有可能导致高估或低估的错误。同样，性别变量的组间差异也存在类似的性质。

第二个表格为 "Marginal Treated Outcome, Untreated Outcome, and Treatment Effect"，分别给出了三种效应的斜率和截距。有了斜率和截距，我们就可以将仅适用于 compliers 人群的 LATE 效应外推到 never-takers 人群和 always-takers 人群。

1
2
3
4
5
6
7
8
Marginal Treated Outcome, Untreated Outcome, and Treatment Effect
           ---------------------------
                  Intercept   Slope  
           ---------------------------
            MTO    965.00    -600.00 
            MUO    550.00    -400.00 
            MTE    415.00    -200.00 
           ---------------------------

第三个表格为 "Average Outcome of Always Takers, Compliers, and Never Takers"，给出不同人群的处理效应和非处理效应。计算方法为利用第二个表 中的结果，分别计算 MTO，MUO 和 MTE 在 \([0, P_C]\)，\([P_C, P_I]\)，\([P_C, 1]\) 三个区间上的期望。

1
2
3
4
5
6
7
8
9
10
Average Outcome of Always Takers, Compliers, and Never Takers
----------------------------------------------------------------------------
                     Always  Compliers  Never    Untreated      Treated  
                     Takers             Takers  Outcome Test  Outcome Test 
                      (1)       (2)      (3)      (2)-(3)       (1)-(2)  
----------------------------------------------------------------------------
 Treated Outcome     860.00   680.00    485.00                   180.00  
 Untreated Outcome   480.00   360.00    230.00     130.00            
 Treatment Effect    380.00   320.00    255.00                       
----------------------------------------------------------------------------

对于 IV 计算出来的 LATE，在这里就等于第（2）列中 \(680-360=320\)。我们同样可以用 IV 回归方法来检验一下结果是否相符。IV 回归的语法和结果如下所示，再次验证了 IV 回归结果仅仅是识别了 compliers 人群的处理效应。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
. ivregress 2sls Y2 (D=Z)

Instrumental variables (2SLS) regression 
                                         Number of obs =    500
                                         Wald chi2(1)  =  52.50
                                         Prob > chi2   = 0.0000
                                         R-squared     = 0.8103
                                         Root MSE      = 120.95
---------------------------------------------------------------
    Y2 |   Coef.  Std. Err.    z    P>|z|  [95% Conf. Interval]
-------+-------------------------------------------------------
     D | 320.000    44.165   7.25   0.000   233.439     406.561
 _cons | 371.000    20.597  18.01   0.000   330.631     411.369
---------------------------------------------------------------
Instrumented:  D
Instruments:   Z

此外，回归结果还包含了两个图形，如下所示。左图为 "Average outcomes"，对应第三个表的结果。右图为 "MTO(p), MUO(p), MTE(p)"，对应第二个表的结果。观察右图，利用处理效应连续性的假定，对于始终 \(D\)=1 的 always Takers，我们也能获得出他的对照组结果 MUO(p) 和处理效应 MTE(p)。而对于始终 \(D\)=0 的 never Takers，我们也能获得他的实验组结果 MTO(p) 和处理效应 MTE(p)。

MTEbinary：LATE 效应的外部效度_Fig2_命令结果_张子楠​

4.2 针对二元工具变量的边际处理效应估计：mtemore​ 命令

mtemore​ 命令安装如下：

1
ssc install mtemore, replace

mtemore​ 命令语法如下：

1
mtemore outcome (endogvar = instrument) [covariates] [, options]

需要注意的是，mtemore​ 中 bootstrap​ 次数不能为 0，最低为 2 次。

1
2
use mtebinary_data.dta, clear
mtemore Y2 (D = Z), summarize(age female) reps(2) graphsave(mtemore)

4.3 针对删失数据的工具变量分位数估计：cqiv​ 命令

cqiv​ 命令安装如下：

1
ssc install cqiv, replace

cqiv​ 命令语法如下：

1
cqiv depvar [varlist] (endogvar = instrument) [if] [in] [weight] [, options]
1
2
3
net get cqiv   //下载数据 alcoholengel.dta 到当前文件夹
use alcoholengel, clear
cqiv alcohol logexp2 nkids (logexp = logwages nkids), quantiles(25 50 75)

六、重要资料和参考链接汇总

‍