微观|第5章:厂商理论—成本理论
【内容速查与目录】
【笔记下载】
一、成本与利润
在经济分析中,成本(cost)被看成是企业对所购买的生产要素的货币支出。
(一)成本
1. 机会成本
机会成本:生产一单位的某种商品的机会成本是指生产者所放弃的使用相同的生产要素在其他生产用途中所能获得的最高收入。
使用资源的机会成本:资源在其他用途中可能得到的最大收益。
理解机会成本:
- 机会成本不等于实际成本,是一种观念上的成本或损失;
- 机会成本是作出一种选择时所放弃的其他若干种可能的选择中最好的一种,是用于其他选择所能得到的最高收入;
- 机会成本并不全是由个人选择所引起的。
机会成本的存在需要三个前提条件:
- 资源是稀缺的;
- 资源具有多种生产用途;
- 资源的投向不受限制。
2. 显成本与隐成本
显成本是指厂商在生产要素市场上购买或租用他人所拥有的生产要素的实际支出(有支付行为),通常包括:雇佣工人、贷款、租用土地的费用等。
隐成本是指厂商本身自己所拥有的且被用于该企业生产过程的那些生产要素的总价格(无支付行为),通常包括:亲自管理企业、使用自己的资金、使用自己的土地等的成本。
在经济学中考察生产成本时,应将隐成本包括在内。企业的所有的显成本和隐成本之和构成总成本。
(二)利润
经济学上的利润指的是经济利润(economic profit)或称超额利润,等于总收益减总成本(含显成本和隐成本)。
正常利润(normal profit)是指厂商对自己所提供的企业家才能的报酬支付,包含在隐成本中。
会计利润(accounting profit)是指厂商的总收益减去显成本以后的余额。
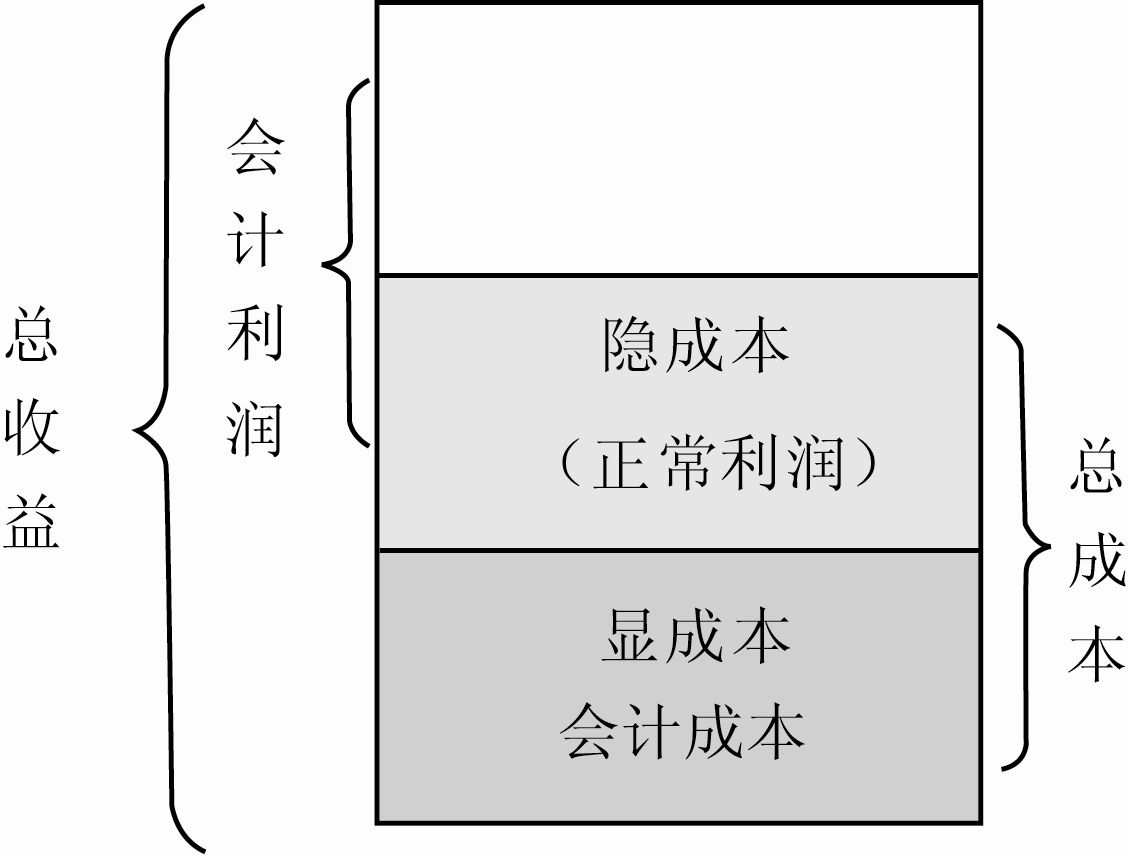
(三)不同成本、利润之间的关系
- 显成本=会计成本
- 隐成本包含正常利润
- 经济成本=机会成本=显成本 + 隐成本
- 经济利润=总收益-经济成本=总收益-机会成本=总收益-(显成本 + 隐成本)
- 会计利润=总收益-显成本
补充:
- 在通常情况下,除企业家才能外,企业的其他生产要素都从市场上购买。此时,正常利润=隐成本。
- 当存在除企业家才能外的自有生产要素时,正常利润 < 隐成本。
二、成本曲线
(一)等成本线
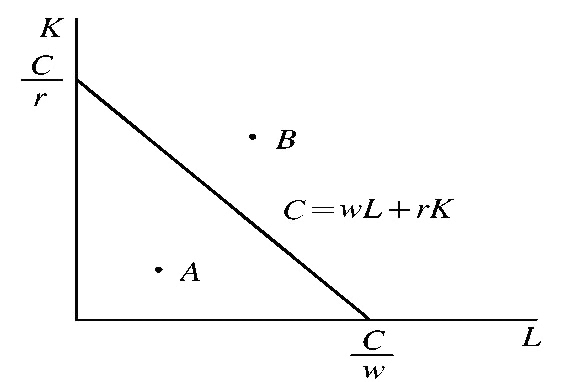
等成本线(Equal-Cost Lines)是在既定的成本和既定生产要素价格条件下,生产者可以购买到的两种生产要素的各种不同数量组合的轨迹。
成本方程:\(C=wL+rK\)
理解补充:
类比"预算约束线",等成本线两侧表示不同的含义:
- 等成本线内(例如 \(A\) 点):要素组合的可行域
- 等成本线外(例如 \(B\) 点):企业无法或不愿意负担的要素组合。
(二)最优要素比例的决定
与消费者理论中的"消费者均衡"类似,厂商理论中也有生产者均衡,目标函数为收益最大化,约束条件为成本约束。
在完全竞争市场中,厂商的利润最大化问题等效于"既定产量的成本最小化"或"既定成本的产量最大化"问题。
1. 既定产量条件下的成本最小化
成本最小化与产量约束:
\[ \begin {align} & \min_{L,K} {\ TC(L,K)}=\min_{L,K} {\ wL+rK} \\ & s.t. \ f(L,K)=f_0 \end {align} \]
构造拉格朗日函数:
\[ \begin {align} \Lambda=wL+rK+\lambda \big [\ f(L,K)-f_0 \big] \end {align} \]
在生产均衡点 \(E\) 有:\(MRTS_{LK}= \frac {MP_L} {MP_K} = \frac w r\)
理解补充:
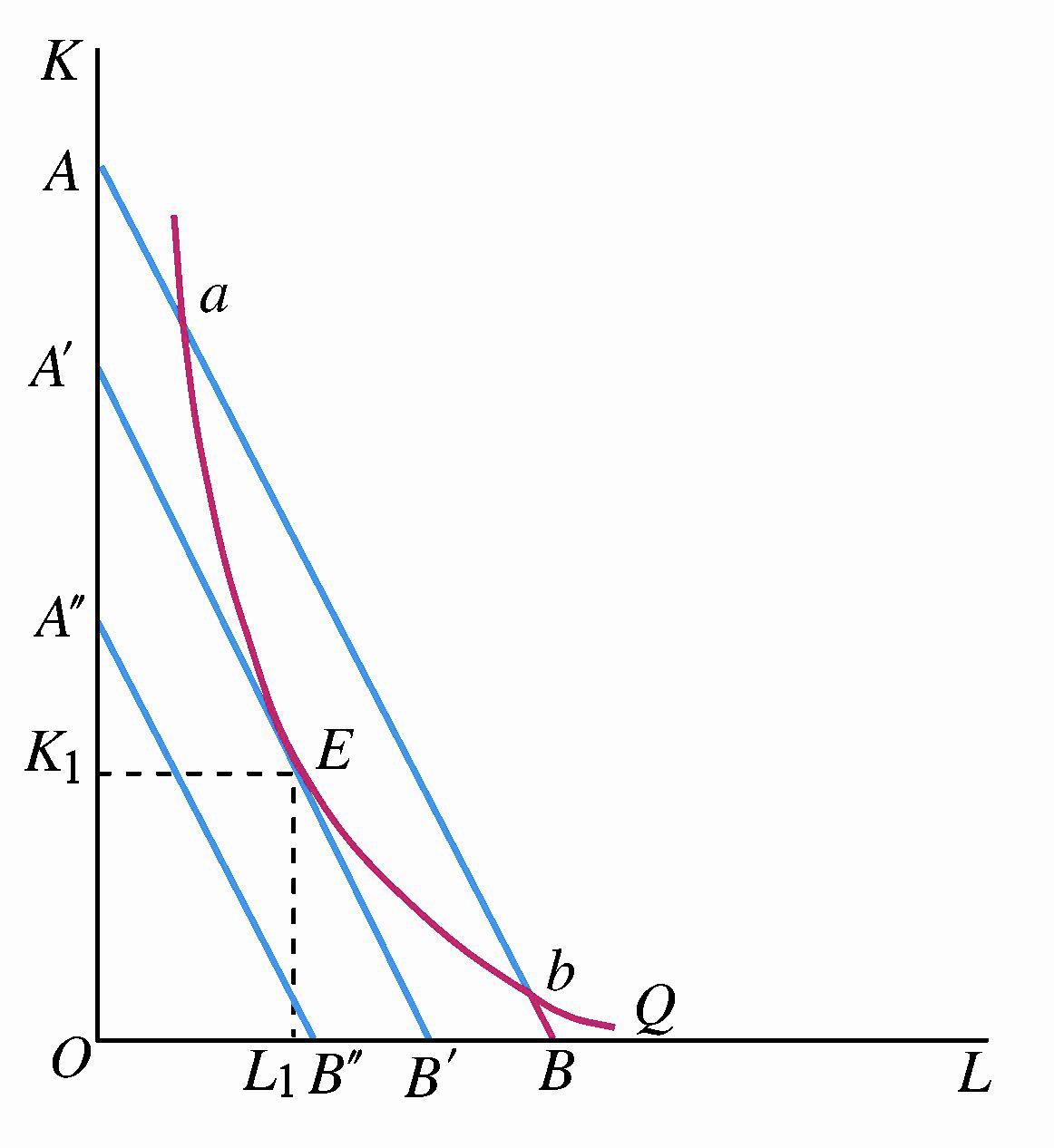
在不变的技术水平下,厂商有明确的产量目标,此时要实现成本最小化,最优生产要素投入为等产量线与等成本线的切点 \(E\)。
- 技术水平不变:多条等成本线平行;
- 既定产量:仅有一条等产量线 \(Q\);
- 成本最小化:在多条等成本线中,选择与等产量线相切的等成本线 \(A'B'\)。
2. 既定成本条件下的产量最大化
产量最大化与成本约束:
\[ \begin {align} & \max_{L,K} \ f(L,K) \\ & s.t. \ wL+rK=C \end {align} \]
构造拉格朗日函数:
\[ \begin {align} \Lambda=f(L,K)+\lambda(C-wL-rK) \end {align} \]
由此可以解得:\(MRTS_{LK}= \frac {MP_L} {MP_K} = \frac w r\)
理解补充:
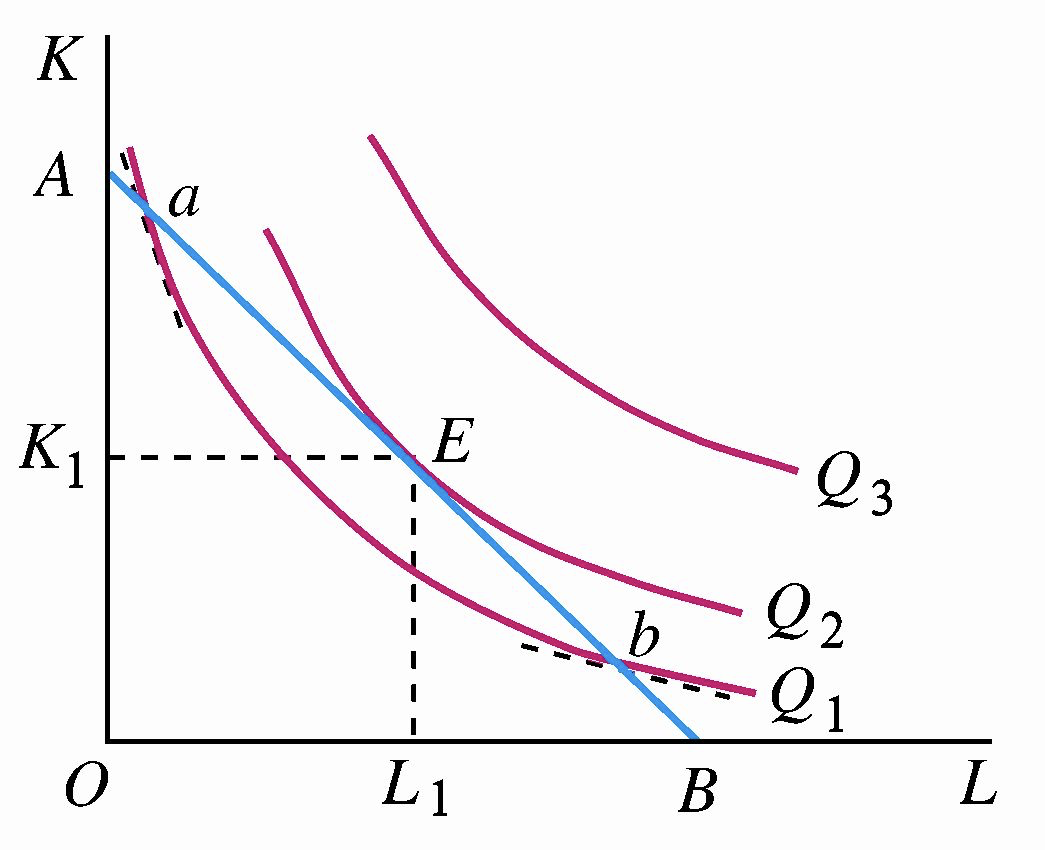
在不变的技术水平下,厂商有明确的成本约束,此时要实现产量最大化,最优生产要素投入为等产量线与等成本线的切点 \(E\)。
- 既定成本:仅有一条等成本线 \(AB\);
- 产量最大化:在多条等产量线中,选择与等成本线相切的等产量线 \(Q_2\)。
3. 小结
不论是既定产量条件下的成本最小化,还是既定成本条件下的产量最大化,在厂商大到均衡时,均有:
\[ MRTS_{LK}= \frac {MP_L} {MP_K} = \frac w r \]
因此,在完全竞争市场中,厂商的利润最大化问题等效于既定产量的成本最小化或既定成本的产量最大化问题。
(二)扩展性和生产总成本
1. 扩展线
在生产要素的价格、生产技术和其他条件不变时,如果企业改变成本,等成本线就会发生平移;如果企业改变产量,等产量曲线就会发生平移。这些不同的等产量曲线将与不同的等成本线相切,形成一系列不同的生产均衡点。这些生产均衡点的轨迹就是"扩展线"(expansion path)。
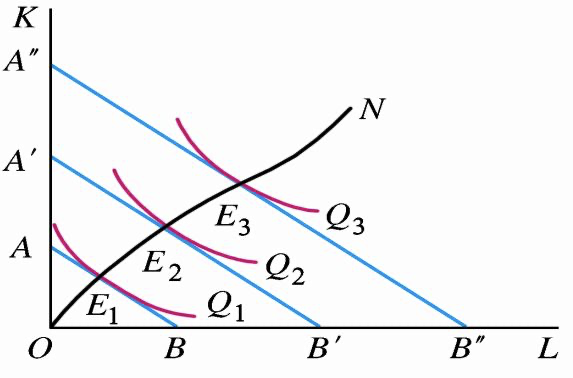
扩展线表示在要素价格不变,技术水平不变的条件下,厂商在长期中,为扩大规模,所可能使用的最佳要素组合所形成的轨迹。
扩展线概念的注意事项:
- 扩展线上所有的点均是生产要素最优组合点,即必须满足 \(\frac {MP_L} {MP_K} = \frac w r\) 条件;
- 扩展线的形状取决于生产函数的形式,不同的生产函数有不同的扩展线。
2. 利润最大化和扩展性
在完全竞争条件下,厂商在追求最大利润的过程中,可以实现扩展性这一长期生产的最优路径的。
在完全竞争条件下,厂商的利润函数为:\(\pi (L,K)= P \cdot f(L,K)-(wL+rK)\)
利润最大化时,一阶条件为:
\[ \left \{ \begin {align} \frac {\partial \pi} {\partial L}=P \cdot \frac {\partial f} {\partial L}-w=0 \notag \\ \frac {\partial \pi} {\partial K}=P \cdot \frac {\partial f} {\partial K}-r=0 \notag \end {align} \right. \]
可以解得:\(\frac {\partial \pi /\partial L} {\partial \pi /\partial K} = \frac {MP_L} {MP_K} = \frac w r\)
3. 扩展性与总成本
长期总成本表示在每一个产量水平上的最小的生产成本。
利用扩展性可以推导得出短期生产总成本。
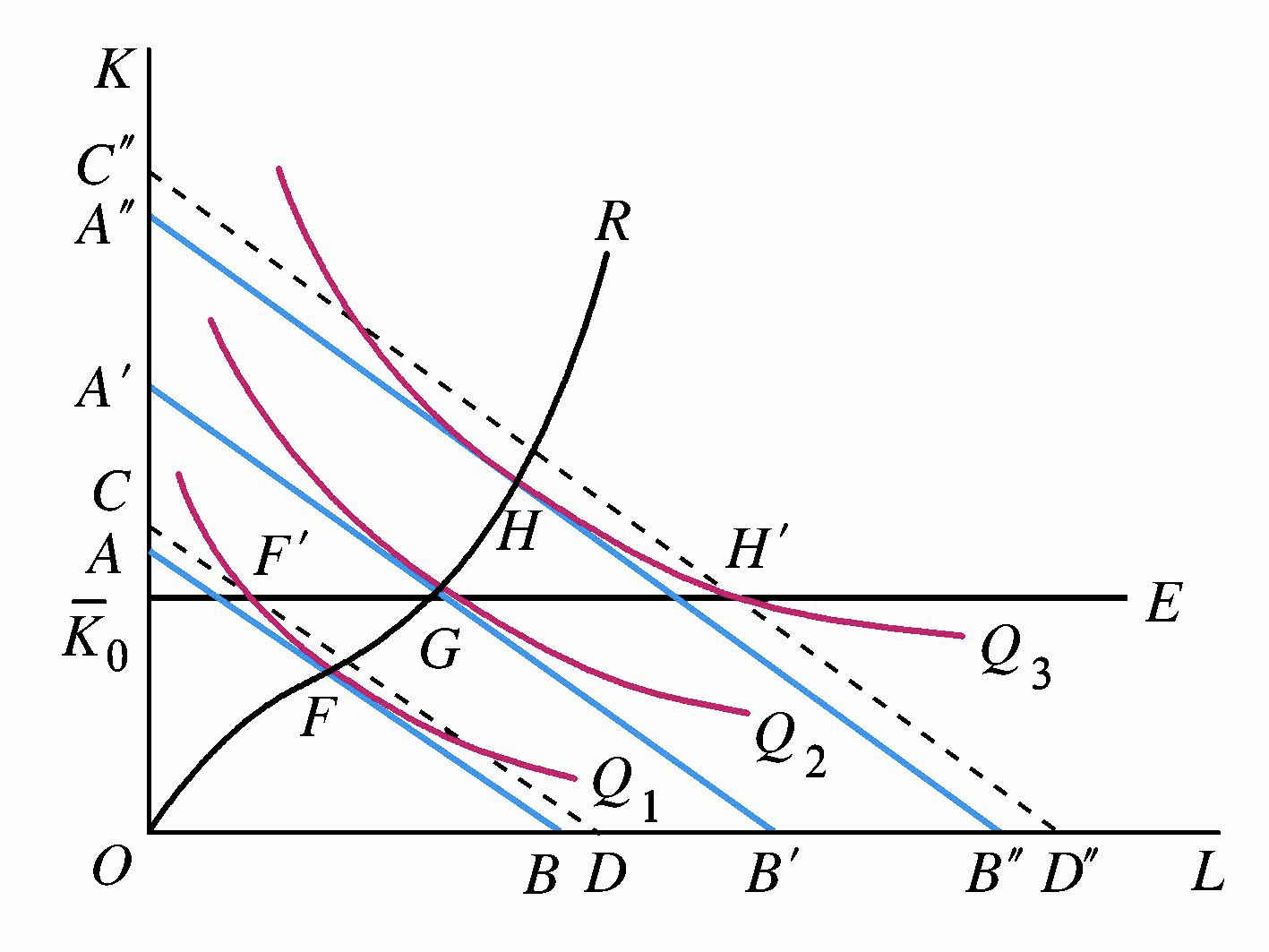
(三)短期成本
1. 由短期生产函数到短期总成本函数
短期总成本函数为:\(STC(Q)= w \cdot L(Q) + r\cdot \overline K\)
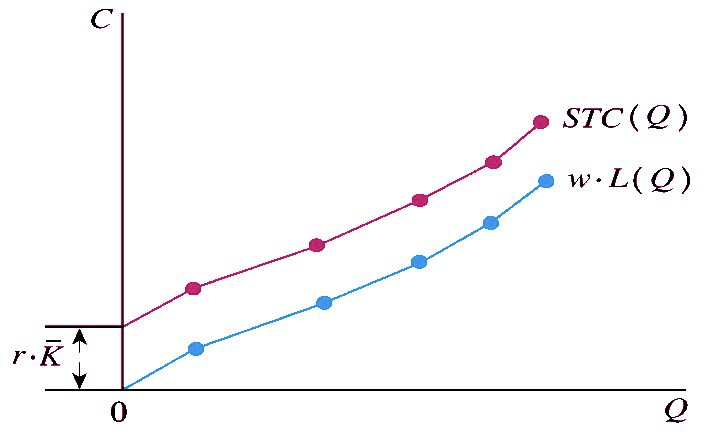
2. 短期成本的分类
在短期,厂商的成本有不变成本部分和可变成本部分之分,具体而言,短期成本有七种。其中,最重要的是边际成本 \(MC\),因为其他成本曲线的形状都是由 \(MC\) 曲线形状来决定的。
总固定成本(\(TFC\)):厂商在短期内为生产一定数量的产品对不变生产要素所支付的总成本。
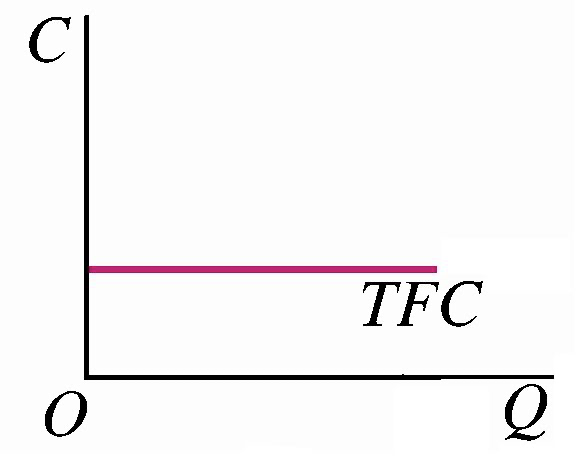
总可变成本(\(TVC\)):厂商在短期内生产一定数量的产品对可变生产要素支付的总成本。
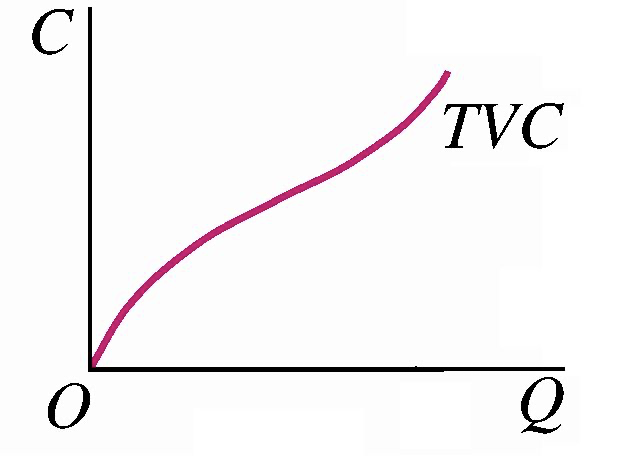
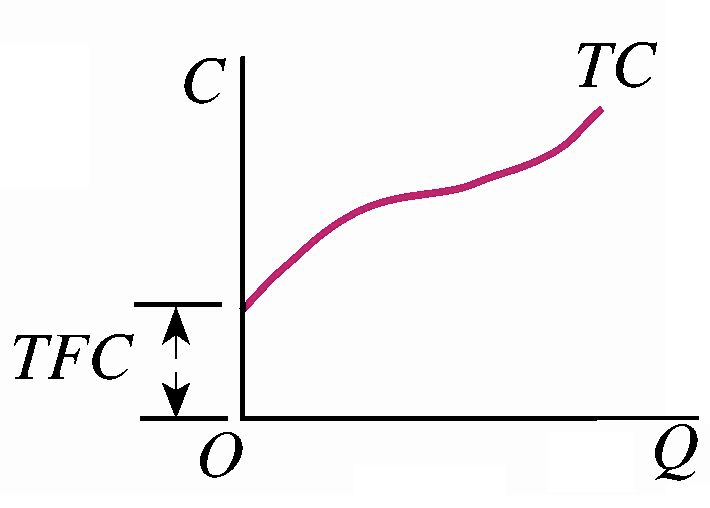
总成本(\(TC\)):厂商在短期内为生产一定数量的产品对全部生产要素所支出的总成本。\(TC=TFC+TVC\),总成本曲线是从纵轴上相当于总固定成本 TFC 高度的点出发的一条向右上方倾斜的曲线。
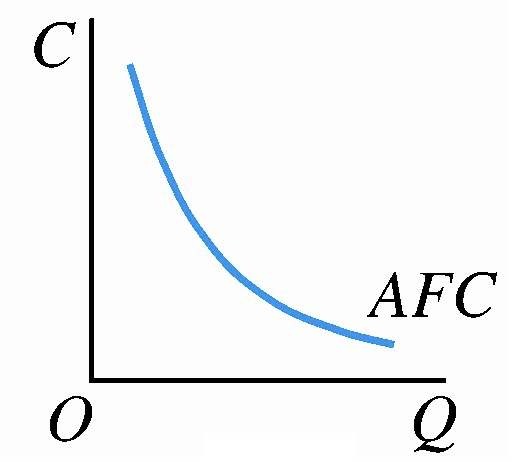
平均固定成本(\(AFC\)):是厂商在短期内平均每生产一单位产品所消耗的不变成本。平均固定成本曲线表示在总固定成本不变的前提下,随着产量的增加,平均固定成本会越来越小。\(AFC=\frac {TFC} Q\)
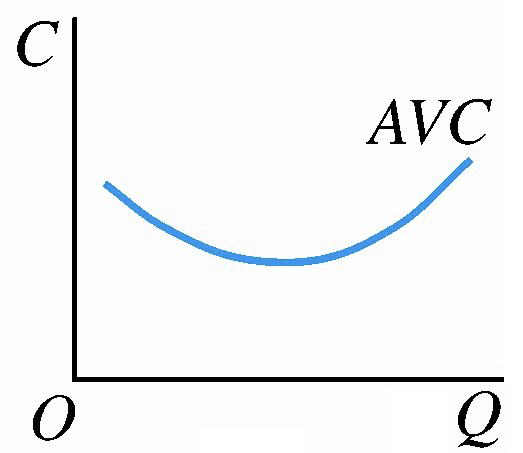
平均可变成本(\(AVC\)):厂商在短期内平均每生产一单位产品所消耗的可变成本。\(AVC=\frac {TVC(Q)} Q\)
平均总成本(\(AC\)):厂商在短期内平均每生产一单位产品所消耗的全部成本,等于平均不变成本和平均可变成本之和。\(AC(Q)=\frac {TC(Q)} Q=AVC(Q)+AFC(Q)\)
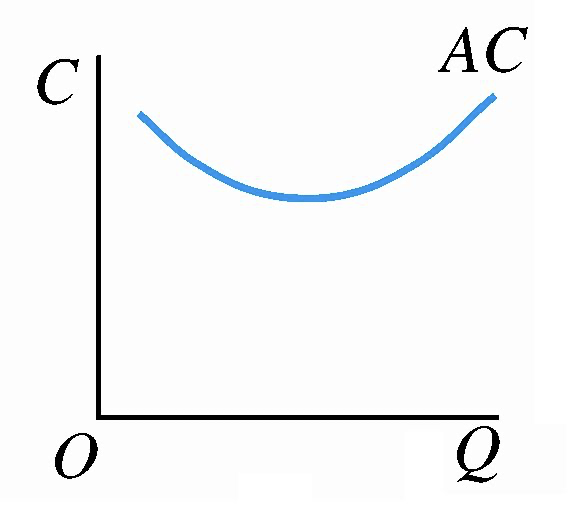
边际成本(\(MC\)):厂商在短期内增加一单位产量时所增加的总成本。在每一个产量水平上的边际成本 MC 值就是相应的总成本曲线的斜率。边际成本曲线呈现出先下降后上升的特征。
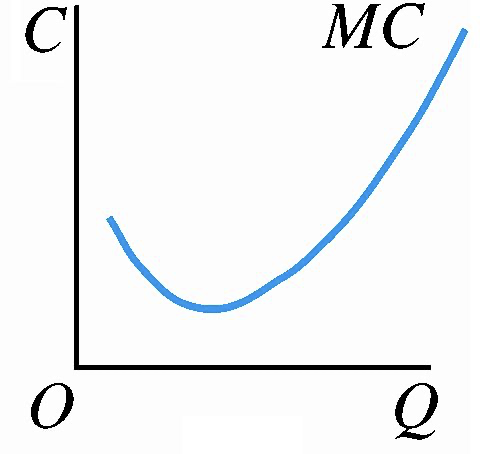
3. 短期成本曲线的综合图
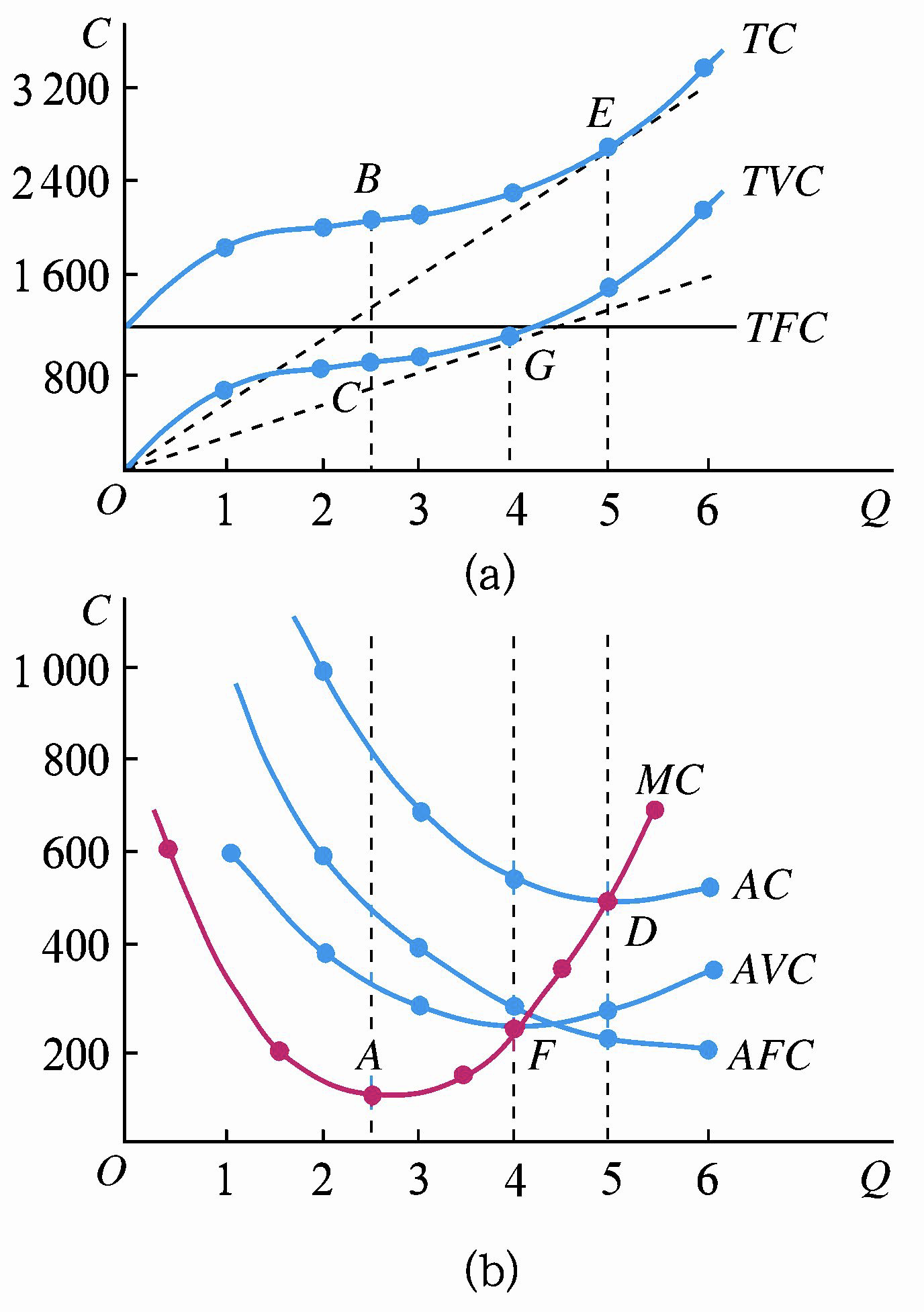
绘图技巧:
- 先绘制边际成本曲线 \(MC\);
- 绘制平均成本 \(AC\) 与平均可变成本 \(AVC\),\(AC\) 与 \(AVC\) 最低点在边际成本 \(MC\) 曲线上,且 \(AC \geq AVC\);
- 绘制呈递减趋势的平均固定成本 \(AFC\),且 \(AC >AFC\)。
4. 短期成本变动的决定因素:边际报酬递减规律
在短期生产中,边际产量的递增阶段对应的是边际成本的递减阶段,边际产量的递减阶段对应的是边际成本的递增阶段,与边际产量的最大值相对应的是边际成本 的最小值。正因为如此,在边际报酬递减规律作用下的边际成本曲线表现出先降后升的 \(U\) 形特征,\(AVC\) 曲线和 \(AC\) 曲线也必定有先降后升的 \(U\) 形特征。而且, \(MC\) 曲线必定会分别与 \(AVC\) 曲线相交于 \(AVC\) 曲线的最低点,与 \(AC\) 曲线相交于 \(AC\) 曲线的最低点。
4.1 边际产量和边际成本之间的关系
短期生产函数:\(Q=f(L,\overline K)\)
短期成本函数:\(STC(Q)=w \cdot L(Q) + TFC\)
因此:\(MC=\frac w { {MP} _L }\),即边际成本 \(MC\) 和边际产量 \({MP} _L\) 两者的变动方向是相反的。
数学补充:
短期成本函数计算过程中涉及反函数的导数求解,反函数的导数是原函数导数的倒数(链接),因此:
\[ \begin{align} SMC=\frac {\partial STC} {\partial Q} = w \cdot \frac {\partial L(Q)} {\partial Q} = w \cdot \Bigg[ \frac {\partial Q(L,\overline K)} {\partial L} \Bigg] ^{-1} = \frac w { {MP} _L} \end{align} \]
4.2 平均产量和平均可变成本之间的关系
短期成本函数:\(TVC(Q)=w \cdot L(Q)\)
平均可变成本函数:$AVC= {Q} = { {AP}_L} $
因此:
- 平均可变成本 \(AVC\) 和平均产量 \(AP_L\) 两者的变动方向是相反的。
- \(MC\) 曲线和 \(AVC\) 曲线的交点与 \(MP_L\) 曲线和 \(AP_L\) 曲线的交点是对应的。
数学补充:
平均产量\(AP_L\)与平均可变成本\(AVC\)关系的推导:
\[ \begin{align} AVC=\frac {SVC} {Q} = \frac {SVC} {L} \cdot \frac {L} {Q} = \frac w {AP_L} \end{align} \]
上式中,使用 \(AP_L = Q / L\) 进行了替换。
在短期内,资本 \(\overline K\) 为固定量,可变生产要素仅有劳动 \(L\),因此 \(SVC=w \cdot L\)。
(四)长期成本
1. 与短期成本函数的比较
短期成本问题表述为:
\[ \begin {align} STC(Q)=\min_{L} \ \{wL+r \overline K\} \end {align} \]
短期生产函数为:\(Q=f(L, \overline K)\),要素价格给定的情况下,成本是产量的函数。
此时短期利润为:\(\pi = PQ-STC(Q)\),厂商追求利润最大化,一阶条件为:
\[ \begin{align} \frac {d\pi} {Q}=P-SMC(Q)=0 \end{align} \]
也就是说,当 \(P=SMC(Q)\) 时,短期要素配置达到最优。
2. 长期成本函数
长期成本问题表述为:
$$
$$
长期生产函数为:\(Q=f(L,K)\)
可得最优要素组合条件为:\(L=L(w,r,Q)\);\(K=K(w,r,Q)\)
长期成本函数为:\(LTC=wL(w,r,Q)+rK(w,r,Q)\)
数学补充:
长期边际成本 \(LMC\) 为:
\[ \begin{align} LMC & = \frac {\partial LTC} {\partial Q} = w \frac {\partial L} {\partial Q} + r \frac {\partial K} {\partial Q} \notag \\ & = \frac w {MP_L} + \frac r {MP_K} \end{align} \]
3. 长期成本曲线
长期总成本 \(LTC\) 是指厂商在长期中在每一个产量水平上通过选择最优的生产规模所能达到的最低总成本。
在要素价格给定的条件下,长期成本曲线为 \(LTC=LTC(Q)\)。
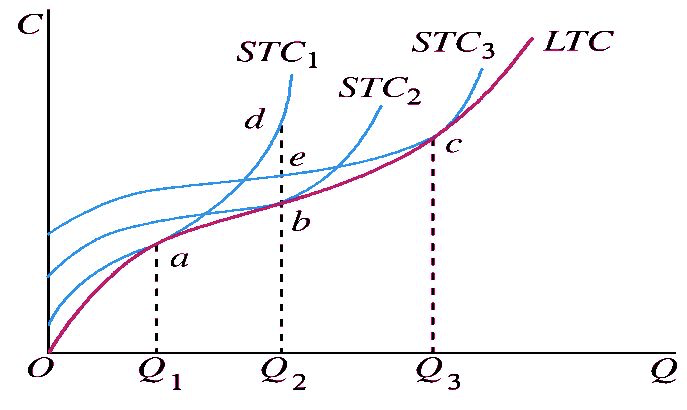
长期总成本曲线是无数条短期总成本曲线的包络线。
长期总成本曲线的特征有:
- 长期总成本曲线从原点出发向右上方倾斜。当产量为零时,长期总成本为零,以后随着产量的增加,长期总成本是增加的。
- 与短期总成本曲线相似的是,长期总成本曲线也是先以递减速率上升,经拐点后以递增的速率上升。
4. 长期平均成本函数和长期平均成本曲线
长期平均成本 \(LAC\) 表示厂商在长期内按产量平均计算的最低总成本。它是厂商在长期内在每一个产量水平上可以实现的最小的平均成本。用数学公式表示为:\(LAC(Q)=\frac {LTC(Q)} {Q}\)
4.1 长期平均成本曲线的形状
长期平均成本曲线是无数条短期平均成本曲线的包络线。
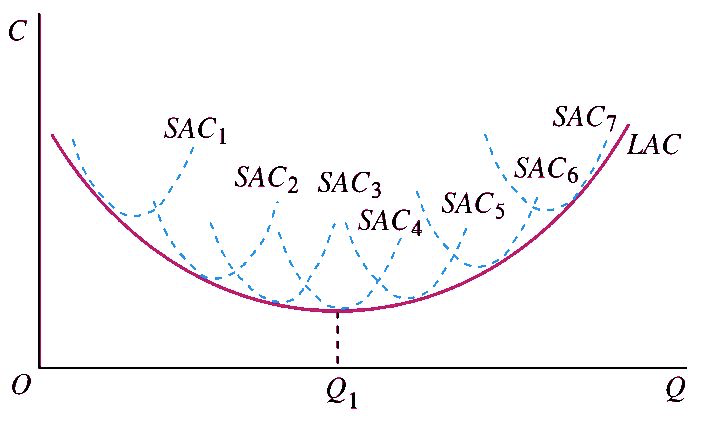
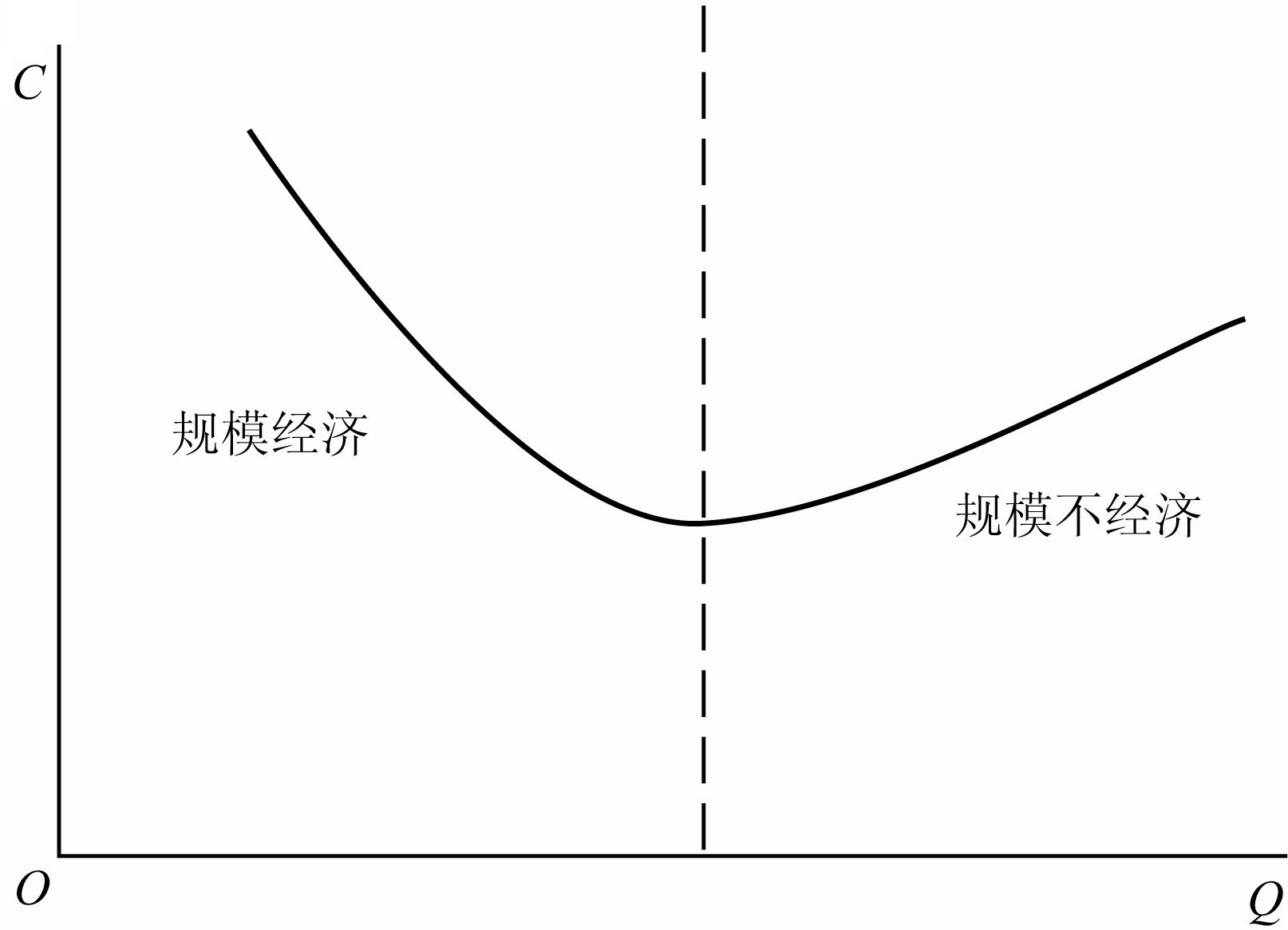
4.2 规模经济与规模不经济
规模经济也被称作为内在经济,即在企业生产扩张的开始阶段,厂商由于扩大生产规模而使经济效益得到提高。或者说,厂商产量增加的倍数大于成本增加的倍数,为规模经济。产生规模经济的主要原因有劳动分工与专业化,以及技术因素。
规模不经济也被称作为内在不经济,即当生产扩张到一定的规模以后,厂商继续扩大生产规模,就会使经济效益下降。或者说,厂商产量增加的倍数小于成本增加的倍数,为规模不经济。
正是由于规模经济和规模不经济的作用,决定了长期平均成本曲线表现出先下降后上升的 \(U\) 形特征。
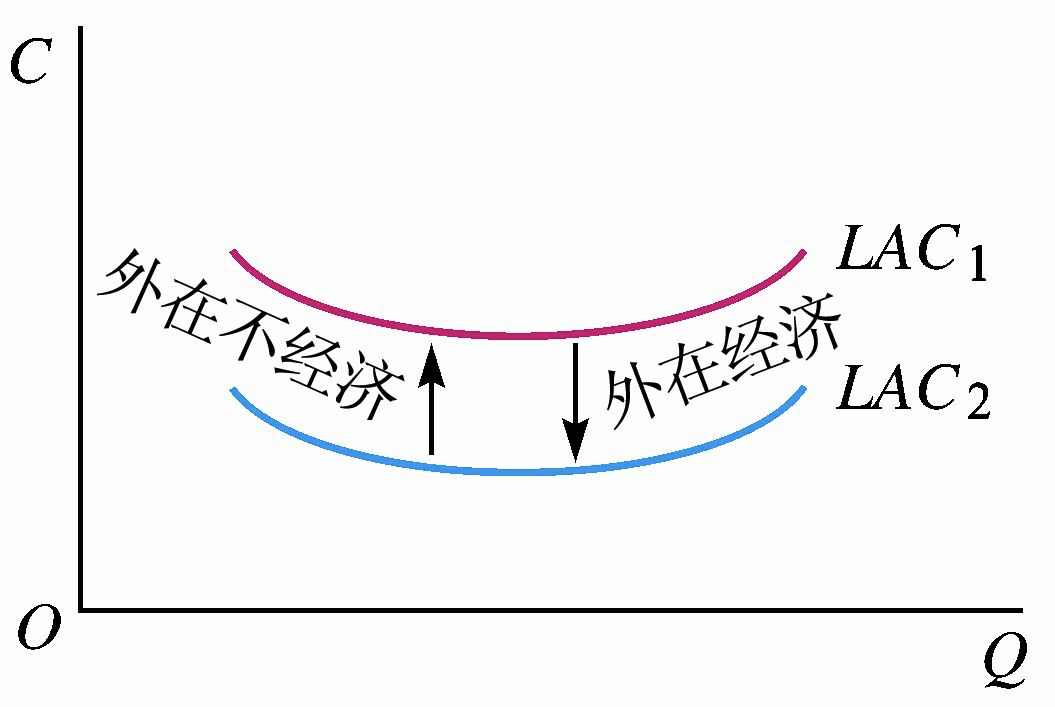
4.3 外在经济与外在不经济(长期平均成本曲线的位置移动)
长期平均成本 \(LAC\) 曲线的位置的变化原因可以用企业的外在经济与外在不经济的概念来解释。
外在经济是由于厂商的生产活动所依赖的外界环境得到改善而产生的,外在不经济是由于厂商的生产活动所依赖的外界环境恶化而产生的。
4.4 长期边际成本函数和长期边际成本曲线
长期边际成本 \(LMC\) 表示厂商在长期内增加一单位产量所引起的最低总成本的增量。
\[ \begin {align} LMC(Q)=\frac {\Delta LTC(Q)} {\Delta Q}=\frac {\partial LTC(Q)} {\partial Q} \end {align} \]
长期边际成本曲线呈 \(U\) 形,它与长期平均成本曲线相交于长期平均成本曲线的最低点。
理解补充:
长期平均成本 \(LAC\) 是短期平均成本 \(SAC\) 的包络线("图示");
不论是长期还是短期:
- 平均成本 \(AC\) 均为先降低后升高;
- 边际成本 \(MC\) 过平均成本 \(AC\) 的最低点;
\(LAC\)、\(LMC\)、\(SMC\)、\(SAC\) 四条曲线相交于 \(LAC\) 最低点。
5. 干中学:降低长期成本
5.1 学习曲线
学习曲线反映了工人经验对生产成本的影响,描绘了企业累积产出与企业生产单位产出所需投入数量之间的关系。
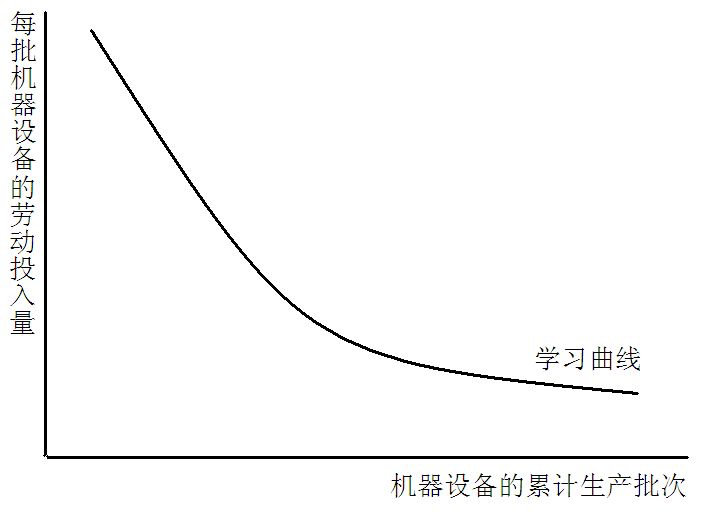
学习曲线表示,随着累计的生产批次的增加,生产每批机器设备所投入的劳动量是递减的,即每批次生产的平均成本是下降的。
学习效应用公式表示为:\(L=A+BN^{-\beta}\)
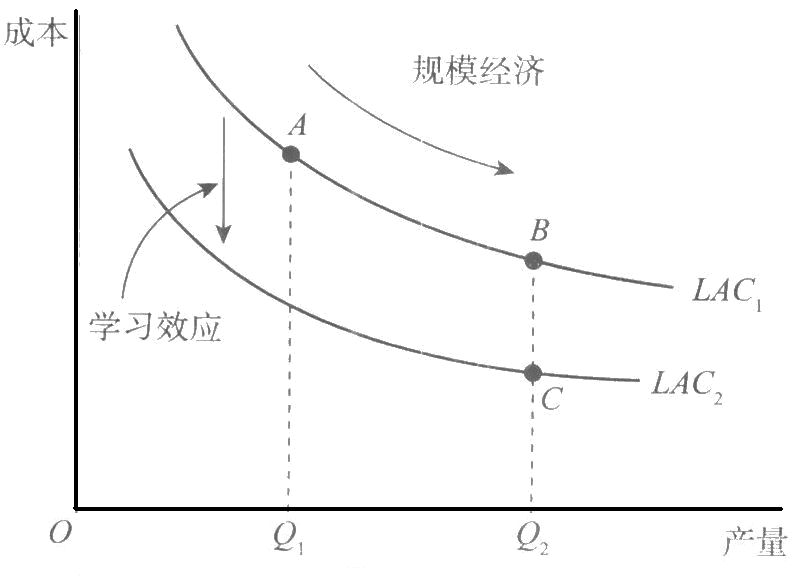
5.2 学习效应与规模效应
当存在着规模经济时(\(LAC_1\) 曲线上由 A 到 B 的移动),平均成本因销售量的增加而逐渐下降,或者平均成本由于学习曲线的存在而下降(由\(LAC_1\)曲线上 B 点移动到\(LAC_2\)曲线上 C 点)。
(五)短期成本曲线与长期成本曲线的关系
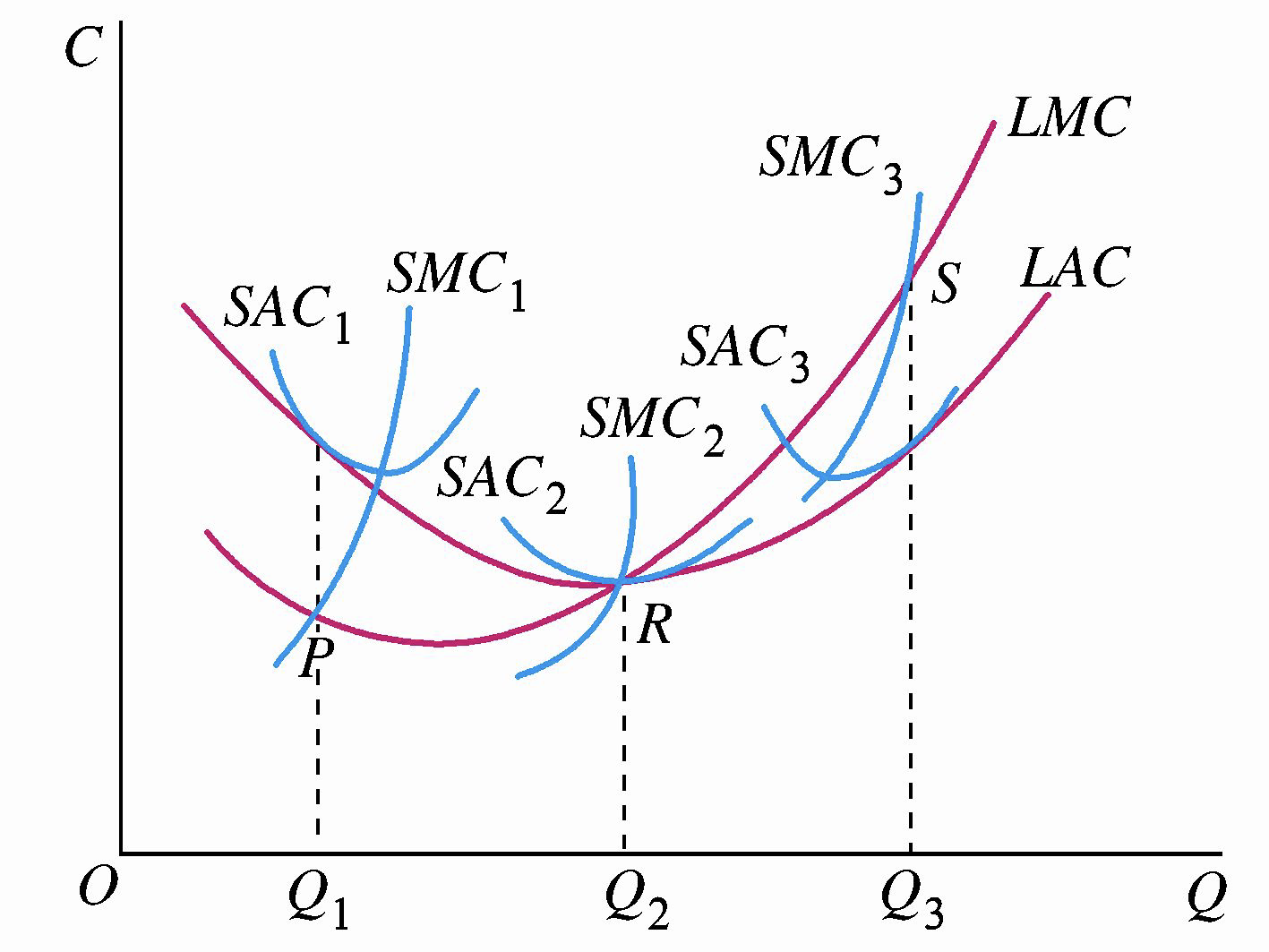
规模经济或规模不经济的情况下,短期成本与长期成本在每一产量水平,都有以下特征:
- 总成本:\(LTC\) 曲线与代表最优生产规模的唯一一条 \(STC\) 曲线相切(\(R\)点);
- 平均成本:\(LAC\) 曲线与代表最优生产规模的唯一一条 \(SAC\) 曲线相切(\(R\)点);
- 边际成本:\(LMC\) 曲线与代表最优生产规模的唯一一条 \(SMC\) 曲线相交(\(R\)点);
- \(LTC\) 曲线的拐点与 \(LMC\) 曲线的最低点相对应;
- \(SMC\) 曲线与 \(SAC\) 曲线相交于 \(SAC\) 曲线的最低点;
- \(LMC\) 曲线与 \(LAC\) 曲线相交于 \(LAC\) 曲线的最低点;
- 存在一条从原点出发的直线与 \(LTC\) 曲线相切,其切点与 \(LAC\) 曲线的最低点相呼应("数学证明");
- 在 \(LAC\) 曲线的最低点,\(LAC\) 曲线与代表最优生产规模的 \(SAC\) 曲线恰好相切于两者的最低点,\(LMC\) 曲线与代表最优生产规模的 \(SMC\) 曲线也恰好相交于这一点。
数学补充:
"第7条"的数学证明:
在长期总成本\(LTC\)曲线中,过原点的直线与\(LTC\)相切,因此在切点处,斜率相等:
\[ \begin{align} \frac {LTC} {Q} = \frac {\partial LTC } {\partial Q} \end{align} \]
其中:左边为直线斜率,右边为长期总成本\(LTC\)斜率。上式可以改写为:
\[ \begin{align} LAC = LMC \end{align} \]
因此该点正好位于\(LAC\)与\(LMC\)的交点处,此时为\(LAC\)的最低点。


相关资源:

