实证|固定效应模型的最新进展
⚠️ 特别注意:本文尚未完成,本文第二、三、四章使用了 chatGPT 辅助阅读,可能存在错误,建议阅读原文。
一、固定效应模型
1. 传统的固定效应估计
在截面数据中,回归法、匹配法估计结果解释为因果效应的基础是要满足非混杂性假设 / 条件独立性假设。但观测数据往往不能涵盖所有的可能影响因素,当存在混杂因素影响时,条件独立性假设不再被满足,可以使用工具变量法,基于阻断后门路径的方式实现因果推断。但工具变量往往很难寻找,且存在一定的工具变量滥用问题。
在面板数据中,可以使用固定效应模型方式识别因果效应。其核心都是尽可能从残差中拿出可以被控制住的部分。
使用固定效应法估计因果效应,应当满足面板数据下的条件独立性假设(CIA):
\[ \begin {align} (Y_{1it},Y_{0it}) \perp D_{it} \ | \ X_{it} , \ U_i, \ t \end{align} \]
如上所示,\(X_{it}\) 表示可观测得混杂因素;\(U_{it}\) 表示不随时间变化的不可观测混杂因素,\(t\) 表示时间。
回归方程可以写为:
\[ \begin{align} Y_{it} =\mu_i + \lambda_t + \tau D_{it} + \overline{X}^\prime_{it} \beta+ \xi_{it} \end{align} \]
在满足上述条件独立性假设(CIA)后,所有随时间变化的混杂因素都可以被观测,通过控制可观测的混杂因素,就可以消除混杂因素对因果效应估计结果的扭曲,得到总体干预组的平均因果效应 ATT。不随时间变化的混杂因素的影响 (即固定效应) 可以通过去均值法或差分法消除。使用去均值法的组间回归方程:
\[ \begin{align} \overline{Y}_i = \mu_i + \overline{\lambda}_t + \tau\overline{D}_i + \overline{X}_i^\prime \beta + \overline{\xi}_i \end{align} \]
其中,\(\overline{x}_i = \frac 1 T \sum^T_{t=1}x_{it}\),\(x\) 表示上式中的 \(Y\)、\(\lambda\)、\(D\)、\(X\) 各变量。因此,组内回归方程为:
\[ \begin{align} Y_{it} -\overline{Y}_i = \lambda_t - \overline{\lambda}_t + \tau(D_{it}-\overline{D}_i) + (X_{it}-\overline{X}_i)^\prime \beta + \xi_{it} - \overline{\xi}_i \end{align} \]
固定效应中涉及的差分法,是干预行为的“事前”与“事后”的差分。
因此,较为常见的固定效应模型的估计方程如下:
\[ \begin{align} Y_{it} =\mu_i + \lambda_t + \tau D_{it} + \beta X_{it} + \xi_{it} \end{align} \]
其中,\(\mu_i\)即为不随时间变化的个体固定效应,\(\lambda _t\)即为不随个体变化的时间固定效应。
2. 固定效应估计的最新进展
引用信息: Ditzen J, Karavias Y. Interactive, Grouped and Non-separable Fixed Effects: A Practitioner's Guide to the New Panel Data Econometrics[J]. Available at SSRN 5365941, 2025.
Ditzen and Karavias (2025) 在SSRN上更新了其最新的工作论文,提出在面板数据中可以使用新的固定效应估计方法,即针对交互固定效应(IFE)、分组固定效应(GEE)和非可分离固定效应(NSTW)估计。
与传统的双重固定效应(TWFE)估计相比,IFE、GEE、NSTW则是通过放宽个体固定效应\(\mu_i\)的假设,企图通过引入新固定效应项进行估计,以实现尽可能控制残差的中可被控制部分的目的。
二、交互固定效应(Interactive Fixed Effects)
1. IFE 估计量
引入交互固定效应,作为对传统个体固定效应模型的拓展。考虑以下线性面板数据模型:
\[ \begin{align} y_{i,t} = x_{i,t}' \beta + c_i + \varepsilon_{i,t} \end{align} \]
其中,\(x_{i,t}\) 是一个 \(K \times 1\) 的观测协变量向量,\(\beta\) 是一个 \(K \times 1\) 的向量,包含了主要关注的参数。标量 \(c_i\) 表示个体效应,包含常数项及其他时间不变变量 \(z_i\):
\[ \begin{align} c_i = z_{i,1}f_1 + \cdots + z_{i,m}f_m = z_i' f \end{align} \]
向量 \(z_i\) 包含观测到的时间不变变量,如常数项、性别、种族、地理位置等,也包括未观测到的变量,如动机、天赋、技术水平、管理技能、地理、生产率等。\(m \times 1\) 的向量 \(f\) 表示这些变量的斜率系数。
在上式中,一个较为严格的假设是:未观测变量 \(z_i\) 与其系数 \(f\) 在时间上是固定的。而交互固定效应(IFE)模型则通过允许 \(f\) 随时间变化,放宽了该假设:
\[ \begin{align} c_{i,t} = z_{i,1}f_{1,t} + \cdots + z_{i,m}f_{m,t} = z_i' f_t \end{align} \]
固定效应(FE)与交互固定效应(IFE)在某些方面是相似的。例如:FE 允许与协变量 \(x_{i,t}\) 存在相关性,IFE 亦如此。此外,在实证研究中,FE 通常并不是主要关注的参数,IFE 亦是如此。最后,和 FE 一样,IFE 若被忽略,将会导致偏误且不一致的估计结果。
一个将在下文讨论中起重要作用的无关参数是 \(m\),即因子的数量。在大多数应用中,\(m\) 是固定且未知的,但固定的 \(m\) 会对具有时变价格的个体效应数量施加限制。NSTW 提出了放松该限制的方法,后文将详细讨论。
在我们进行估计之前,有必要将公式 (1) 和 (3) 以矩阵形式重写,即在时间维度上堆叠数据:
\[ \begin{align} y_i = X_i \beta + u_i \end{align} \]
\[ \begin{align} u_i = F z_i + \varepsilon_i \end{align} \]
其中,\(y_i = (y_{i,1}, y_{i,2}, \dots, y_{i,T})'\),\(u_i = (u_{i,1}, u_{i,2}, \dots, u_{i,T})'\),\(\varepsilon_i = (\varepsilon_{i,1}, \varepsilon_{i,2}, \dots, \varepsilon_{i,T})'\)都是 \(T \times 1\) 的向量;\(\beta\) 是 \(K \times 1\) 的系数向量;\(F = (f_1, f_2, \dots, f_m)'\) 是一个 \(T \times m\) 的公共因子矩阵;\(z_i = (z_{i,1}, \dots, z_{i,m})'\) 是 \(m \times 1\) 的因子载荷向量。在下文中,我们假设 \(F\)、\(z_i\) 和 \(X_i\) 与 \(\varepsilon_i\) 独立,但 \(Fz_i\) 可以与 \(X_i\) 有关。
如果 \(T > N\),该系统可以被视为“似乎无关的回归”(Seemingly Unrelated Regressions, SUR),可采用 Zellner(1962)提出的可行广义最小二乘法(FGLS)进行估计,并允许跨个体单位之间的协方差结构比 IFE 模型更为灵活。然而,在面板数据中通常为 \(N > T\) 的情况,此方法将变得不可行。但如果 \(F\) 中的因子是可观测的,那么一致的普通最小二乘估计量(OLS)为:
\[ \begin{align} \hat{\beta}_{IFE} = \left( \sum_{i=1}^N X_i' M_F X_i \right)^{-1} \left( \sum_{i=1}^N X_i' M_F y_i \right) \end{align} \]
其中,\(M_F\) 是正交投影矩阵,\(M_F = I_T - F(F'F)^{-1}F'\),\(I_T\) 是 \(T \times T\) 的单位矩阵。当 \(F = (1, 1, \dots, 1)'\) 时,该估计量退化为组内固定效应估计量(within-groups or fixed effects estimator)。不幸的是,\(F\) 中的因子通常是不可观测的,因此上述 OLS 估计器在实际中是不可行的。
2. 估计方法
交互固定效应(IFE)模型被广泛应用于建模面板数据中的未观测异质性,特别适用于捕捉单位间共享但表现方式各异的时间变化因素。第4.1节系统评述了当前主流的IFE估计方法,主要包括七种方法,它们在假设要求、计算难度与适用性上各具特点。
2.1 ILS / Quasi-MLE(迭代最小二乘 / 准最大似然)
代表文献:Bai (2009), Moon & Weidner (2017)
使用场景:适用于大N大T的数据结构,理论研究常用。
优点:
- 允许协变量与因子交互项相关;
- 理论基础完善;
缺点:
- 需事先设定因子个数 \(m\);
- 迭代过程可能收敛困难;
- 小样本偏差明显,动态模型表现较差。
2.2 Penalized Least Squares(惩罚最小二乘,PLS)
代表文献:Lu & Su (2016)
使用场景:因子数量未知,需在估计中自动选择\(m\)。
优点:
- 基于LASSO惩罚,自适应选择\(m\);
- 在强因子假设下具oracle性质;
缺点:
- 不适用于序列相关误差;
- 依赖初始估计,敏感性高。
2.3 PNNR(后核范数正则化)
代表文献:Moon & Weidner (2019)
使用场景:解决ILS估计中非凸性导致的局部极小问题。
优点:
- 将秩约束转化为核范数,实现全局收敛;
- 不需预设\(m\),估计更稳健;
- 可扩展为后续迭代的起点;
缺点:
- 初步估计收敛速度慢;
- 稍慢于ILS的收敛率(略低于 \(\sqrt{NT}\));
2.4 IV估计器(工具变量方法)
代表文献:Cui et al. (2022)
使用场景:适用于含滞后变量、存在内生性的模型。
优点:
- 避免优化迭代与偏差;
- 适用于滞后解释变量;
缺点:
- 假设协变量与因子存在线性关系;
- 需要构造合适工具变量。
2.5 IPF(无附带参数偏差的IV)
代表文献:Juodis & Sarafidis (2022)
使用场景:短T或固定T面板,含滞后变量。
优点:
- 避免Nickell偏差与估计\(n\)个载荷;
- 可在有限时间维度下使用;
缺点:
- 实施复杂;
- 需构造代理因子或工具变量。
2.6 CCEP(Common Correlated Effects Pooled Estimator)
代表文献:Pesaran (2006)
使用场景:适用于存在横截面依赖的广义模型。
优点:
- 使用截面平均变量近似因子;
- 不需估计\(m\);
- 简单、稳健;
缺点:
- 秩条件严格(\(m \leq K+1\));
- 动态面板存在偏差,需进一步修正。
2.7 TACCE(Time-Averaged CCE)
代表文献:Westerlund et al. (2025)
使用场景:适用于小N面板,如国家、省份、行业数据。
优点:
- 避免使用横截面平均,适合固定N;
- 可用于小样本稳健性分析;
缺点:
- 尚处发展阶段,理论支撑较弱。
2.8 估计方法比较
| 方法名称 | 是否估计\(m\) | 偏差 | 是否适用于滞后项 | 优势 | 局限 |
|---|---|---|---|---|---|
| ILS | ✘ | 有 | 一般 | 理论成熟 | 小样本偏差,敏感迭代 |
| PLS | ✔ | 有 | ✘ | 自动选\(m\) | 不适用于动态模型 |
| PNNR | ✔ | 可校正 | ✔ | 稳健收敛 | 初估慢,较复杂 |
| IV | ✔ | 无 | ✔ | 无偏估计 | 假设强 |
| IPF IV | ✔ | 无 | ✔ | 可用短T,稳健 | 构造工具变量复杂 |
| CCEP | ✘ | 有(可修正) | ✔ | 实用简便 | 依赖秩条件 |
| TACCE | ✘ | 少 | ✔ | 小N适用 | 理论待丰富 |
三、分组固定效应(Grouped Fixed Effects)
1. GFE 估计量
若未观测的异质性不是在个体之间变化,而是在个体组之间变化,那么将个体划分为组可以提升估计效率。分组固定效应(Grouped Fixed Effects, GFE)是交互固定效应(IFE)的一种特殊情形,适用于如班级、学校、国家等天然存在聚类结构的情境中(参见 MacKinnon 等,2023)。
我们遵循 GFE 文献,假设总体中存在 \(G\) 个组,单位 \(i\) 的组归属由 \(g_i = g\) 决定,其中 \(g \in \{1, 2, \dots, G\}\)。例如,如果单位 \(s\) 属于第 \(j\) 组,则有 \(g_s = j\)。此时,公式(3)可改写为:
\[ c_{i,t} = I\{g_i = 1\} f_{1,t} + \cdots + I\{g_i = G\} f_{G,t} \]
其中 \(I\{\cdot\}\) 表示指标函数。GFE 是 IFE 的一个特殊情形,此时因子载荷等于组别归属的指标函数,每一个因子仅作用于对应的一组单位。在上述表达中,可设 \(z_{i,g} = I\{g_i = g\}\),且 \(G = m\)。
GFE 设定对模型估计具有重要影响:个体效应的数量从 \(O(N)\) 降低为 \(O(G)\),其中 \(G\) 是较小且固定的常数。因此,GFE 避免了附带参数问题(incidental parameters problem)以及动态面板中的Nickell 偏误。
若组别归属已知,则 \(\beta\) 的 GFE 估计量可由公式(6)给出,并因组别结构而得到简化。
2. 估计方法
分组固定效应模型(GFE)旨在缓解传统固定效应模型对每个个体单独设置一个固定效应所引发的维度灾难和估计效率低问题。GFE 假定所有个体被划分为 \(G\) 个组,同组内个体共享相同的固定效应。其形式如下:
\[ y_{i,t} = x_{i,t}'\beta + \alpha_{g_i,t} + \varepsilon_{i,t} \]
其中,\(g_i \in \{1, ..., G\}\) 表示个体 \(i\) 所属的组,\(\alpha_{g,t}\) 为组别时间效应。
2.1 K-Means + FE 两步法(Bonhomme & Manresa, 2015)
使用场景:个体固定效应呈现有限结构,适用于大\(N\)和中等\(T\)的面板数据。
方法流程:
- 初始分组(如随机或依据协变量);
- 固定组别估计组效应;
- 固定组效应重新分配组别;
- 重复迭代,直到收敛。
优点:
- 减少估计参数数量(从\(N\)降为\(G\));
- 捕捉异质性更有结构性;
- 实证上识别“行为类型”或“制度簇”;
缺点:
- \(G\) 需提前设定,若设错可能误分;
- 非凸问题,依赖初始分组,可能陷入局部最优;
- 组内异质性仍无法完全建模。
2.2 Penalized Estimation / Shrinkage-Based GFE(Su et al., 2016)
方法特征:
- 利用惩罚函数(如 Lasso)自动确定个体组别;
- 模型中隐含聚类目标;
优点:
- 无需预设\(G\);
- 可以在大样本中识别组数及结构;
缺点:
- 对调参依赖强;
- 惩罚项设置过大会误分组;
- 理论上需强组内同质性假设。
2.3 Panel Classification Estimator(Ando & Bai, 2016)
核心思想:在面板回归中结合分组选择与参数估计,利用分组的截面均值与时间均值来识别。
使用场景:有截面聚类结构但缺乏预先分组变量的设定。
优点:
- 比K-means方法更稳健;
- 适合用于单向或双向固定效应;
缺点:
- 方法偏理论,实证中应用尚少;
- 实现相对复杂,依赖均值变换步骤的正确性。
2.4 GFE with Time Trends / Dynamics(Bonhomme, Lamadon & Manresa, 2022)
模型扩展:允许组固定效应中包含时间趋势,如:
\[ \alpha_{g,t} = \mu_g + \delta_g \cdot t \]
使用场景:各组可能经历不同的时间路径(如经济增长、制度演化)。
优点:
- 增强模型解释力;
- 更贴近实际政策/制度变化的路径依赖;
缺点:
- 参数数量上升;
- 趋势设定可能过于刚性;
- 高度依赖趋势假设的结构正确性。
2.5 估计方法比较
| 特征 | 表现 |
|---|---|
| 维度降低 | 将 \(N\) 个个体效应降至 \(G \ll N\) |
| 解释性强 | 可识别“类群”、“制度类型” |
| 政策分析适用 | 常用于地区、国家、公司等聚类异质性研究 |
| 可与动态模型结合 | 可处理组异质趋势,适配IFE扩展 |
四、非分离双重固定效应(Non-separable Two-Way Fixed Effects)
1. NSFE 估计量
Bonhomme 等(2022)提出了一个更一般形式的未观测异质性模型:
\[ c_{i,t} = h(z_i, f_t) \]
其中 \(h(\cdot, \cdot)\) 是一个光滑的实值函数。若 \(h(z_i, f_t) = z_i' f_t\),该模型就包含了 IFE 作为一个特例;而若 \(h(\cdot, \cdot)\) 是非线性的,那么 NSTW 提出的模型相较 IFE 更具一般性。
例如,未观测异质性可以采取恒定相对风险厌恶(constant relative risk aversion)或恒定替代弹性(constant elasticity of substitution, CES)形式。比如:
\[ h(z_i, f_t) = \left(d z_i^\gamma + (1 - d) f_t^\gamma\right)^{1/\gamma}, \quad \text{当 } m = 1。 \]
此外,NSTW 还解决了 IFE 的一个限制:在价格随时间变化的设定下,个体效应数量 \(m\) 不应过大相对于 \(N\) 与 \(T\),否则模型的适用性将受限。对于传统固定效应模型,一个 \(z_i\) 就可以表示无限多个时间不变的未观测特征,因此不对个体效应数量加以限制。
但若这些特征的“价格”随时间异质性变化,则特征数量也需受限,构成约束。以增长回归为例,个体效应可能反映以下因素:法律制度与司法效率、殖民历史与制度演化、政治体制、文化规范、内陆国家状态、种族分化、语言差异、气候带与自然资源禀赋等。
气候变化、技术进步与地缘政治结构的变化可能提高某些特征的价格、降低另一些特征的价格,从而使得 IFE 模型在 \(m\) 固定的情形下不再适用。观察期越长,多个个体特征经历价格变动的可能性越高。
Chudik 等(2011)早期的研究提出了如下模型:
\[ c_{i,t} = \sum_{j=1}^m z_{i,j} f_{j,t} + \sum_{j=m+1}^{N} x^{w}_{i,j} f^{w}_{j,t} \]
其中包含两类因子:前 \(m\) 个是强因子 \(f_{j,t}\),后 \(N - m\) 个是弱因子 \(f^{w}_{j,t}\),其在 \(N \to \infty\) 时趋于无限。假设这些弱因子与解释变量不相关,则称为交互随机效应(interactive random effects)。
因此,模型(9)可以称为交互混合效应模型(interactive mixed effects),融合了 IFE 与交互随机效应的特征。
在实证中,引入无限多个弱因子并不具有约束性(见 Onatski, 2010;Freeman and Weidner, 2023),但假设它们与解释变量不相关则是一种限制。
在较弱的正则条件下,模型(8)可被视为一个无限 IFE 模型的近似形式:
\[ c_{i,t} = \sum_{j=1}^{\infty} z_{i,j} f_{j,t} \]
该形式不再对 \(c_{i,t}\) 与解释变量之间的相关性加以限制(见 Freeman and Weidner, 2023)。因此,不可分的未观测异质性模型(non-separable unobserved heterogeneity model)可以被理解为含有无限个个体效应和因子的 IFE 模型。
2. 估计方法
传统的固定效应(FE)、交互固定效应(IFE)与分组固定效应(GFE)模型,通常假设个体固定效应是可加性或线性的。然而,在很多经济现象中,个体特征与时间特征之间可能存在非线性交互作用,从而导致异质性效应无法简单拆解为 \(z_i + f_t\) 或 \(z_i^\top f_t\) 的形式。这就引出了 不可分未观测异质性模型(Nonseparable Unobserved Heterogeneity Models) 。
此类模型的一般形式为:
\[ y_{i,t} = x_{i,t}'\beta + h(z_i, f_t) + \varepsilon_{i,t} \]
其中,\(h(z_i, f_t)\) 是未知的非线性函数,不能表示为可加或线性可分的形式。该类模型可以看作 IFE 模型在非线性设定下的推广。
2.1 Tensor Product Sieve Estimator(Zhu et al., 2021)
基本思想:使用张量乘积B样条函数逼近 \(h(z_i, f_t)\) 的非线性形式。
使用场景:\(z_i\) 与 \(f_t\) 均为低维连续变量,适用于 \(N,T\) 都较大的设定。
估计步骤:
- 对 \(h(z_i, f_t)\) 使用 B 样条函数展开;
- 利用最小二乘法估计系数;
- 采用交叉验证选择基函数数量;
优点:
- 函数逼近能力强;
- 理论性质较完善;
缺点:
- 维数诅咒严重;
- 不适用于高维 \(z_i\) 或 \(f_t\);
- 实证中调参较复杂(如节点选择)。
2.2 Neural Network Approach(Chang et al., 2023)
基本思想:将 \(h(z_i, f_t)\) 的估计转化为神经网络函数拟合问题。
使用场景:当非线性关系复杂或未知时,用深度学习逼近。
估计步骤:
- 构建多层感知器网络(MLP)表示 \(h(\cdot)\);
- 与线性部分联合训练;
- 使用梯度下降进行拟合;
优点:
- 表达能力强,适应性好;
- 自动捕捉复杂交互关系;
缺点:
- 缺乏可解释性;
- 收敛依赖调参、初始化;
- 模型选择缺乏明确准则;
- 无法明确识别因子结构。
2.3 Interactive Fixed Effects Approximation(Freeman & Weidner, 2023)
基本思想:将非线性 \(h(z_i, f_t)\) 用无限多个线性因子展开来逼近:
\[ h(z_i, f_t) \approx \sum_{j=1}^M \lambda_{i,j} f_{j,t} \]
并在 \(M \to \infty\) 时收敛到真正的不可分函数。
使用场景:当 \(h(\cdot)\) 为未知但满足光滑性条件时。
优点:
- 理论严密;
- 与传统 IFE 模型兼容;
- 允许多样的非线性结构;
缺点:
- 在有限样本下 \(M\) 的选择不明确;
- 难以保证数值收敛;
- 不具备自动模型选择功能。
2.4 估计方法比较
| 方法 | 表达能力 | 可解释性 | 调参难度 | 理论完备性 | 适用范围 |
|---|---|---|---|---|---|
| Tensor Sieve | 中 | 高 | 中 | 完备 | 低维非线性 |
| Neural Network | 高 | 低 | 高 | 尚不充分 | 任意非线性结构 |
| IFE Approximation | 中高 | 中 | 中 | 完备 | 通用近似方式 |
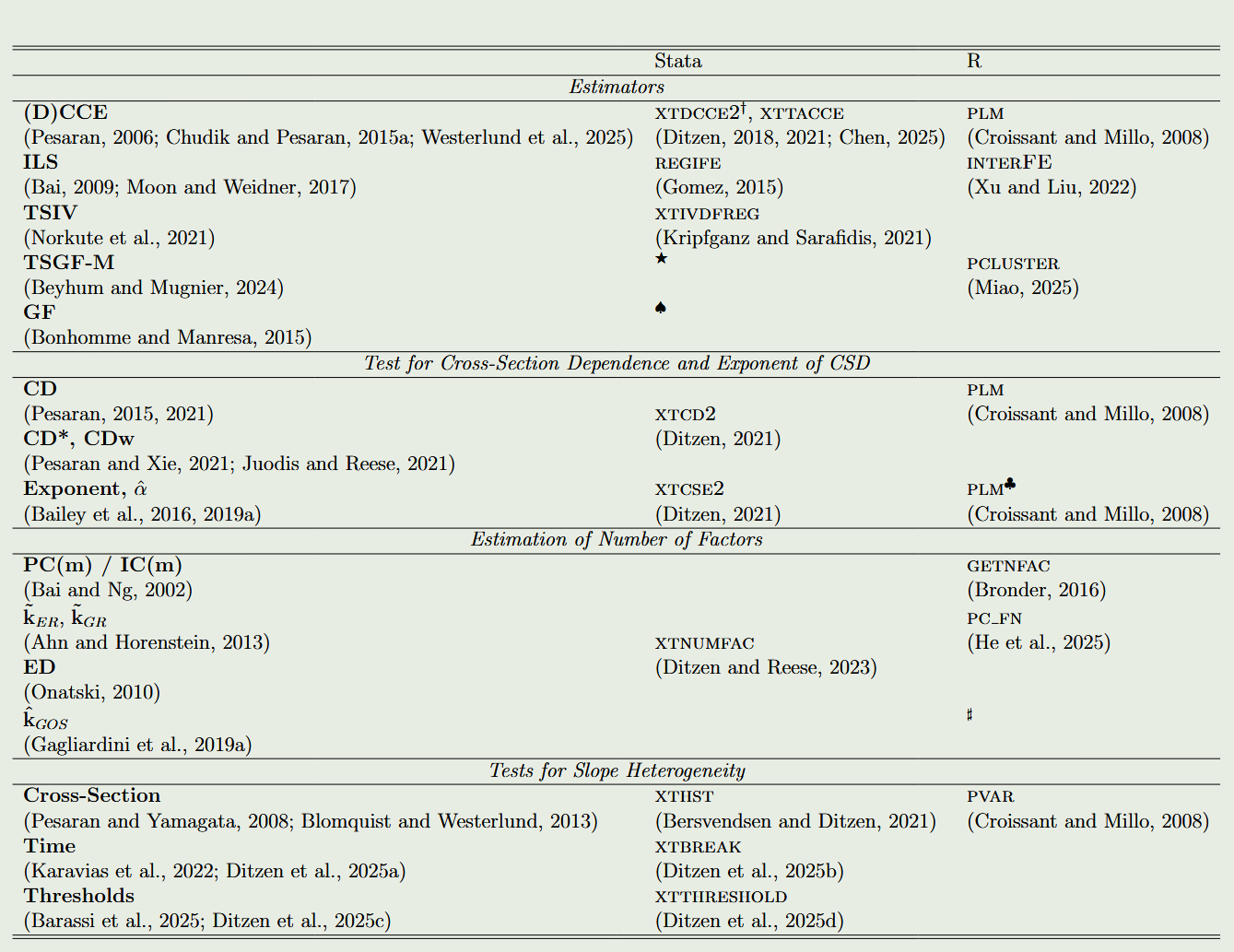
五、命令实现
已经有一些Stata和R命令可以实现上述固定效应模型。