一、厂商

（一）企业的性质

　　科斯在论文《企业的性质》中提出了“交易成本”概念。在科斯看来，企业和市场是两种不同的资源配置方式。在企业内，“权威”指导资源的配置；在市场上，价格配置资源。市场的运行是有成本的，通过形成一个组织，并允许某个权威（一个“企业家”）来支配资源，就能节约某些市场运行成本，即企业的性质是价格机制的替代物。

　　企业存在的理由：

交易活动内部化，降低交易成本；
带来规模经济；
促进劳动分工。

（二）厂商的目标：

　　在微观经济学中，一般总是假定厂商的目标是利润最大化。这一基本假定是“经济人”假设在生产理论中的具体化。

　　在现代公司制度中，企业所有者与经营者相分离，这可能导致企业所有者与经营者目标分歧。在信息不对称和信息不完全的情况下，厂商可能追求个人目标最大化、销售收入最大化或市场销售份额最大化来替代利润最大化，这就偏离了利润最大化的目标。

补充：（网页链接）

信息不完全：市场主体不拥有某种经济环境状态的全部知识，其获取的或掌握的信息不足以使市场主体作出理性判断或决策。

信息不对称：一些人比另外一些人具有更多的有关经济信息，可看作是信息不完全中的特殊情况。

二、生产函数

（一）生产要素

1. 生产要素的概念

　　生产要素：在生产中投入的各种经济资源，包括劳动、土地和资本等。生产要素一般划分为劳动、土地、资本和企业家才能四种。

　　劳动：人类在生产过程中提供的体力和智力的总和。

　　土地：不仅指土地本身，而且包括地上与地下的一切自然资源。

　　资本：表现为实物形态（资本品或投资品）与货币形态。

　　企业家才能：企业家组织建立和经营管理企业的才能。

2. 生产函数

2.1 生产函数的概念

　　生产函数：在一定时期内，在一定技术条件下，生产中所使用的各种生产要素的数量与所能生产的最大产量之间的关系。

$\begin {align} Q=f(L,K) \end {align}$

2.2 短期生产与长期生产

　　在微观经济学中，短期和长期的划分以生产者能否变动全部要素投入的数量作为标准。

　　短期（short run）指生产者来不及调整全部生产要素的数量，至少有一种生产要素的数量是固定不变的时间周期。

　　短期生产函数可写为：$Q=f(L,\overline K)=f(L)$

　　长期（long run）指生产者可以调整全部生产要素的数量的时间周期。

　　长期生产函数可表示为：$Q=f(L, K)$

3. 短期生产函数

3.1 总产量、平均产量和边际产量

　　劳动的总产量 $TP_L$ 指与一定的可变要素劳动的投入量相对应的最大产量，即 $TP_L=f(L,\overline K)$

　　劳动的平均产量 $AP_L$ 指平均每一单位可变要素劳动的投入量所生产的产量，即 $AP_L=\frac {TP_L} L$

　　劳动的边际产量 $MP_L$ 指增加一单位可变要素劳动投入量所增加的产量，即 $MP_L= \frac {\Delta TP_L} {\Delta L} = \frac {\partial TP_L} {\partial L}$

3.2 边际报酬递减规律

　　在技术水平不变的条件下，在连续等量地把某一种可变生产要素增加到其他一种或几种数量不变的生产要素上去的过程中，当这种可变生产要素的投入量小于某一特定值时，增加该要素投入所带来的边际产量是递增的；当这种可变要素的投入量连续增加并超过这个特定值时，增加该要素投入所带来的边际产量是递减的。

　　边际报酬递减规律的三个方面注意事项：

边际报酬递减规律是以技术不变为前提的，如果技术水平提高，边际报酬可以递增。
边际报酬递减规律是以其他要素不变为前提的。
它是在某种要素（如劳动）增加达到一定程度之后才出现的。

　　从理论上讲，边际报酬递减规律成立的原因在于：对于任何产品的短期生产来说，可变要素投入和固定要素投入之间存在着一个最佳的数量组合比例。

3.3 短期生产的三个阶段

第 Ⅰ 阶段（$O \to L_3$）：平均产量递增阶段。该阶段 $MP_L>AP_L>0$，$TP_L$ 与 $AP_L$ 不断上升；
第 Ⅱ 阶段（$L_3 \to L_4$）：平均产量递减阶段。该阶段 $AP_L \gt MP_L \gt 0$，$TP_L$ 不断上升，$AP_L$ 逐渐下降（要素投入最佳区域/经济区域）；
第 Ⅲ 阶段（$L_4 \to \infty$）：边际产量为负阶段。该阶段 $AP_L \gt 0 \gt MP_L$，$TP_L$ 与 $AP_L$ 逐渐下降。

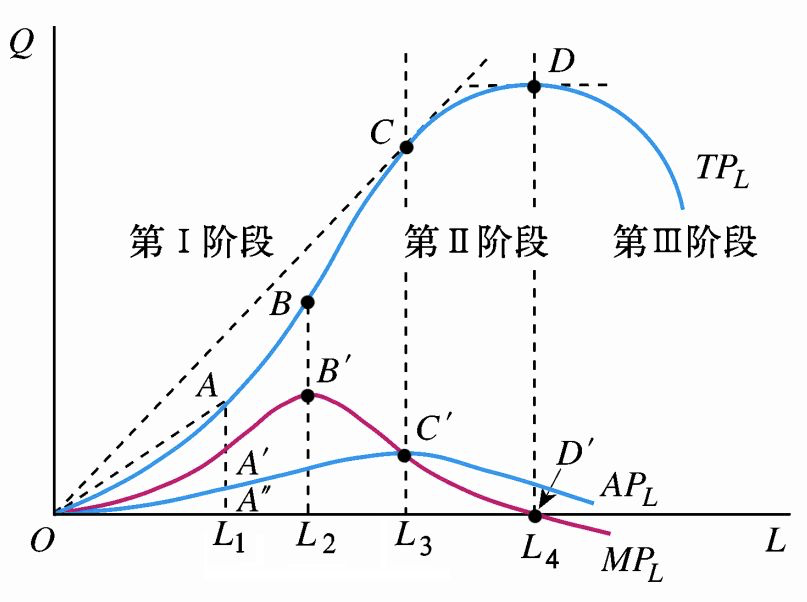
总产量、平均产量与边际产量的相互关系

B点处，$MP_L$最大；
C点处，$AP_L$最大；
D点处，$TP_L$最大。

4. 长期生产函数

4.1 等产量曲线

　　等产量曲线（isoquant）是在技术水平不变的条件下，生产同一产量的两种生产要素投入量的所有不同组合的轨迹。与等产量曲线相对应的生产函数为：$Q=f(L,K)=Q^0$

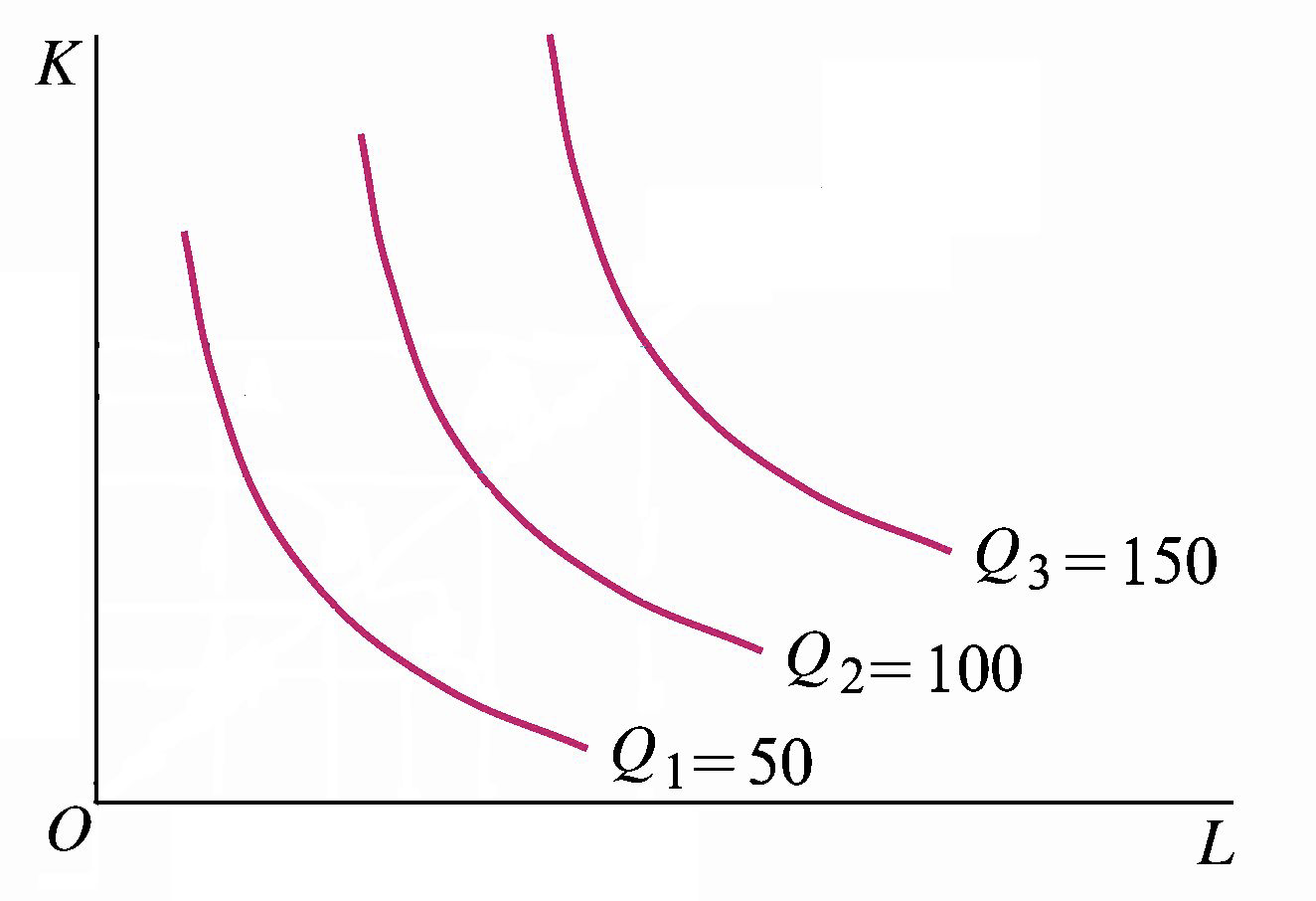
等产量曲线

　　等产量曲线的性质：

表示某一生产函数的等产量曲线图中，可以画出无数条等产量曲线，并且任意两条等产量曲线不能相交；
由于边际技术替代率递减，因此等产量曲线一般都凸向原点。

联系补充：

等产量曲线类似于“无差异曲线”。

两者区别：

等产量曲线表示产量，无差异曲线表示效用；

等产量曲线是客观的，无差异曲线是主观的。

4.2 边际技术替代率

　　在维持产量水平不变的条件下，增加一单位某种生产要素投入量时所减少的另一种要素的投入数量，被称为边际技术替代率（Marginal Rate of Technical Substitution，MRTS）。劳动对资本的边际替代率的定义公式为：

$\begin {align} MRTS_{LK} = - \frac {\Delta K} {\Delta L} \end {align}$

　　等产量曲线上某一点的边际技术替代率是等产量曲线在该点斜率的绝对值。边际技术替代率还可以表示为两种要素的边际产量之比，即$MRTS_{LK} = - \frac {\Delta K} {\Delta L} = \frac {MP_L} {MP_K}$，证明如下：

　　设生产函数为：$Q=f(L,K)$，对生产函数两边都取全微分，有：$dQ=\frac {\partial f} {\partial L} dL + \frac {\partial f} {\partial K} dK$

　　等产量曲线上的产量相同，即$dQ=0$，因此：$MRTS_{LK} = - \frac {d K} {dL} = \frac {\partial f / \partial L} {\partial f / \partial K} = \frac {MP_L} {MP_K}$

4.3 边际技术替代率递减规律

　　在维持产量不变的前提下，当一种生产要素的投入量不断增加时，每一单位的这种生产要素所能替代的另一种生产要素的数量是递减的。

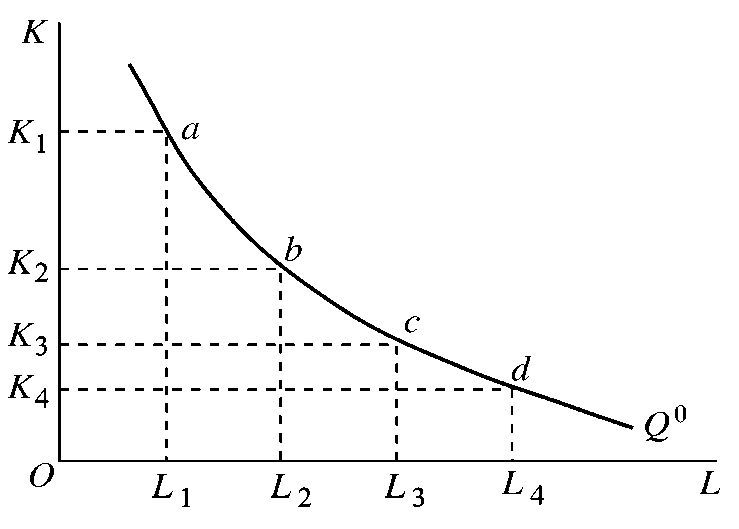
边际技术替代率递减

　　边际技术替代率递减的主要原因在于：任何一种产品的生产技术都要求各要素投入之间有适当的比例，这意味着要素之间的替代是有限制的。

5. 等产量曲线的具体形状

5.1 固定替代比例的生产函数（线性生产函数）

　　固定替代比例的生产函数表示在每一产量水平上任何两种生产要素之间的替代比例都是固定的。生产函数的通常形式为：$Q=aL+bK$，相对应的等产量曲线是一条直线。（传送门：“完全替代品”）

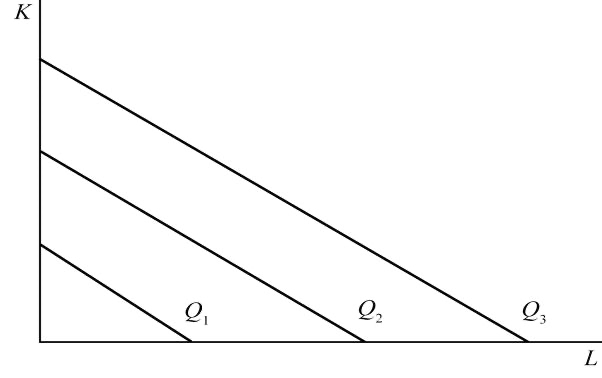
固定替代比例的生产函数

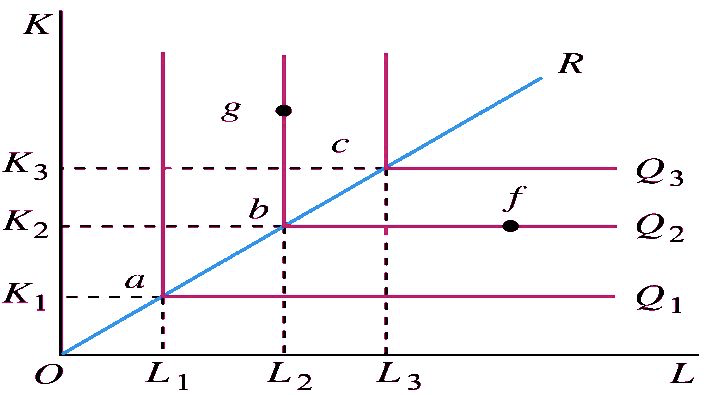
5.2 固定投入比例的生产函数（里昂惕夫生产函数）

　　固定投入比例生产函数表示在每一个产量水平上任何一对要素投入量之间的比例都是固定的。生产函数的通常形式为：$Q=\min \left\{ \frac L u, \frac K v \right\}$，相对应的等产量曲线为 L 型，最优投入要素组合为 L 型的拐点。（传送门：“完全互补品”）

固定投入比例的生产函数

5.3 柯布-道格拉斯生产函数（C-D 生产函数）

　　柯布-道格拉斯生产函数（C-D 生产函数）是最常见的一种生产函数，其一般形式为：$Q=AL^{\alpha} K^{\beta}$

　　C-D生产函数的主要特征：

　　第一，$\alpha$和$\beta$分别表示劳动和资本在生产过程中的相对重要性，或者说是表示劳动所得和资本所得在总产量中所占的份额。

　　$L \cdot MP_L = L \cdot \alpha A L^{\alpha -1} K^{\beta}=\alpha AL^{\alpha} K^{\beta} = \alpha Q$，即$\frac {L \cdot MP_L } {Q}=\alpha$

　　$K \cdot MP_K = K \cdot \beta A L^{\alpha } K^{\beta-1}=\beta AL^{\alpha} K^{\beta} = \beta Q$，即$\frac {K \cdot MP_K} {Q}=\beta$

　　第二，$A(\lambda L)^{\alpha} (\lambda K)^{\beta}=A \lambda^{\alpha + \beta} L^{\alpha} K^{\beta}$，$\lambda \gt 1$。

若$\alpha + \beta \gt 1$，为规模报酬递增；
若$\alpha + \beta \lt 1$，为规模报酬递减；
若$\alpha + \beta =1$，为规模报酬不变。

5.4 规模报酬

5.4.1 规模报酬变化的含义

　　规模报酬变化是指在其他条件不变的情况下，企业内部各种生产要素按相同比例变化时所带来的产量变化。

5.4.2 规模报酬的三种类型

　　产量增加的比例大于各种生产要素增加的比例，称之为规模报酬递增，即$f(\lambda L, \lambda K) \gt \lambda f(L,K)$；

　　产量增加的比例等于各种生产要素增加的比例，称之为规模报酬不变，即$f(\lambda L, \lambda K)=\lambda f(L,K)$；

　　产量增加的比例小于各种生产要素增加的比例，称之为规模报酬递减，即$f(\lambda L, \lambda K) \lt \lambda f(L,K)$。

5.4.3 等产量曲线与规模报酬

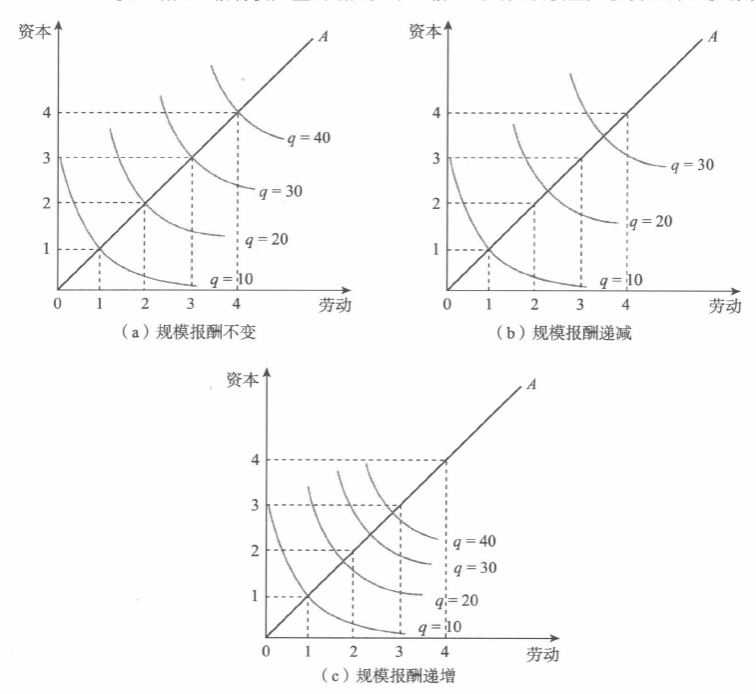
三种规模报酬

补充：

规模报酬不变：从变动比例上看，$要素投入=产出$

规模报酬递减：从变动比例上看，$要素投入>产出$

规模报酬递增：从变动比例上看，$要素投入<产出$

5.4.4 规模报酬变化的规律

　　当企业从最初的很小的生产规模开始逐步扩大的时候，企业面临的是规模报酬递增的阶段。在企业得到了由生产规模扩大所带来的产量递增的全部好处以后，一般会继续扩大生产规模将生产保持在规模报酬不变的阶段。这个阶段有可能比较长。在这以后，企业若继续扩大生产规模，就会进入一个规模报酬递减的阶段。

5.5 扩大生产规模的最优路径

　　扩展线（expansion curve）——类比““收入—消费曲线””

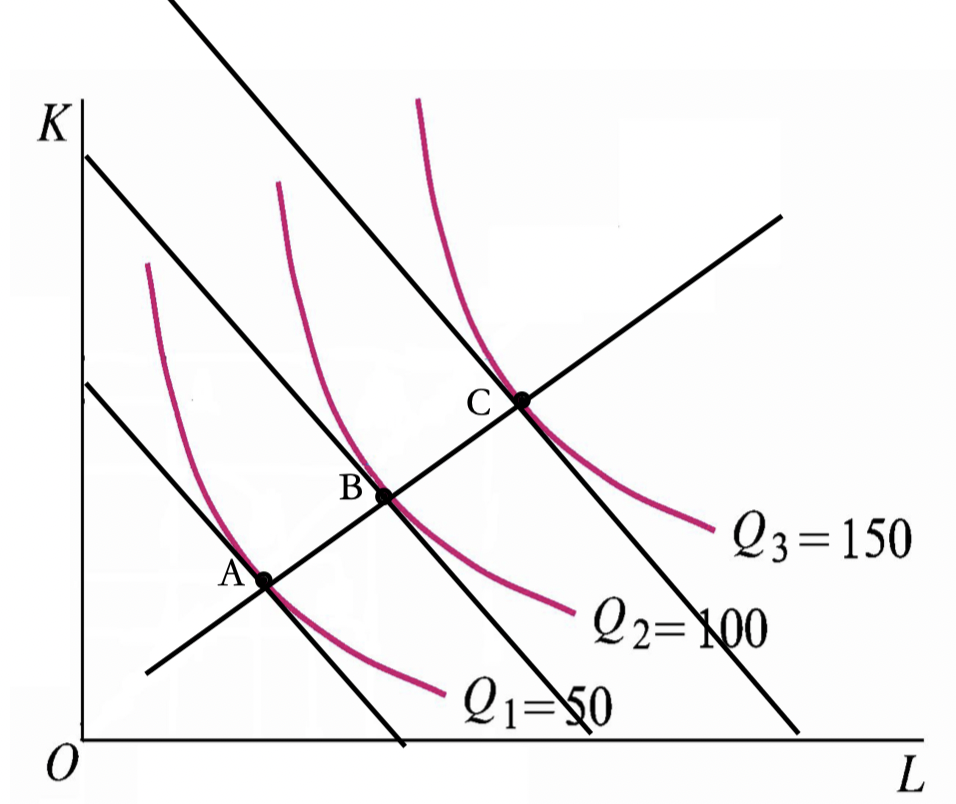
　　扩展线是：

不同生产规模下，生产要素最优组合点的轨迹；
生产规模扩大的最优路径。

　　对于不同的等产量曲线与等成本线的切点的连线（例如：A、B、C），为扩大生产规模的最优路径。

扩大生产规模的最优路径

　　‍

相关资源：