发展经济学|附录A5-利用常规生产函数的解释
1. 调整后的常规生产函数 (meta-production function)
使用常规生产函数可以解释工业化初级阶段到高级阶段增长类型变化。常规生产函数在超长期的生产关系中,包含了因无形资本积累引起的技术创新和投入品质量改进的影响。常规生产函数可以被理解为新古典生产函数的包络线。
假定产出 \(Y\) 由两种要素生产出来:质量调整后的劳动力 \(X=EL\),质量调整后的资本投入 \(Z=HK\)。两种生产要素都使用边际效率衡量:
\[ \begin{align} Y=M(X,Z) \end{align} \]
- 质量调整后的劳动 \(X=EL\):\(E\) 为劳动生产效率,\(L\) 为常规度量的劳动力(如工作时间);
- 质量调整后的资本 \(Z=HK\):\(H\) 为资本生产效率,\(K\) 为常规度量的资本。
因此,要素的相对价格为:
\[ \begin{align} \frac w r =\frac {vE} {qH}= \frac {E} {H} \cdot \frac {v} {q} \end{align} \]
2. 要素替代弹性
\(E\) 和 \(H\) 表示劳动和资本的“增加量”或“增长系数”。在经济增长的数学分析中,将 \(EL\) 和 \(HK\) 作为生产函数中的要素投入是很常见的。在上述生产函数中,技术可以根据资源结构的变化做出调整。例如,当 \(E\) 随教育投资而上升,\(X\) 相对于 \(Z\) 提高了。
\(M\) 为一个长期生产函数,在长期,\(X\) 和 \(Z\) 的边际生产率 \(MP_X\) 和 \(MP_Z\) 不会下降,技术进步可以发挥充分的作用,\(X\) 和 \(Z\) 之间的替代弹性是非常大的。
\(X\) 和 \(Z\) 之间的替代弹性:
\[ \begin{align} \sigma = \frac { \Delta X / X} { \Delta Z / Z } = \frac Z X \cdot { \frac { \Delta X} { \Delta Z} } \end{align} \]
在竞争性市场中(新古典的假设下),要素的替代弹性 \(\sigma = \frac Z X \cdot { \frac { \Delta X} { \Delta Z} } = \frac Z X \cdot { \frac w r }\)(传送门:MRTS)。
然而,考虑到技术进步对资本和劳动的作用不同,\(X\) 和 \(Z\) 之间的替代弹性 \(\sigma\) 不是要素投入比例变化率 \(G( Z/X )\) 与工资-利率比例变化率 \(G(w/r)\) 之间的比例。按常规度量的工资率 \(w\) 是不熟练劳动力报酬 \(v\) 和劳动生产效率增长率 \(E\) 的乘积,按常规度量的利率 \(r\) 是边际资本报酬 \(q\) 和资本生产效率增长率 \(H\) 的乘积。因此,要素替代弹性为:
\[ \begin{align} \sigma = \frac { G(Z/X) } { G(v/q) } = \frac { \left \{ [G(K) + G(H)] - [G(L) + G(E)] \right \} } { [G(v) - G(q)] } \end{align} \]
补充:
上面考察的弹性,是要素相对利用量对要素相对报酬变化的弹性,原因是技术进步导致要素利用发生变化,是通过相对要素报酬变化引致的。这里要素替代弹性计算过程类似于需求收入弹性。
- 分子:要素相对投入量的变化,\(G(Z/X) =\frac { \Delta (Z/X) } { (Z/X) }\)
- 分母:要素相对报酬的变化,即非熟练工与边际资本的报酬之比:\(G(v/q) =\frac { \Delta (v/q) } { (v/q) }\)
考虑到生产函数一般为指数形式,在计算增长率或变化率等指标时,使用对数微分法可以较为简单地计算出相关增长率。例如要计算 \(X\) 的增长率,先对 \(X\) 取对数变成 \(\ln X\),然后对时间 \(t\) 进行微分,那么 \(X\) 的增长率 \(G(X)\) 为:
\[ \begin{align} G(X)= \frac {\partial \ln X } {\partial t } = \frac {\partial \ln X } {\partial X } \cdot \frac {\partial X } {\partial t } = \frac { \dot X } {X } \end{align} \]
其中,\(\dot X\) 为 \(t\) 期 \(X\) 的增长量(相对于 \(t-1\) 期),即 \(\dot X = \Delta X= X_t - X_ {t-1}\)。
因此,原弹性计算公式的分母可以改写为:
\[ G(v/q) = \frac {\partial \ln (v/q) } {\partial t } = \frac {\partial \ln (v) } {\partial t } - \frac {\partial \ln (q) } {\partial t } = G(v) - G(q) \]
同理,分子也可以改写为:
\[ { G(Z/X) } = \frac {\partial \ln (HK/EL) } {\partial t } = [G(K) + G(H)] - [G(L) + G(E)] \]
3. 图解: 技术变化与要素投入
如下图所示,曲线 \(m\) 表示等产量线。假设技术变化不改变等产量曲线 \(m\),以技术进步和人力资本提高为目的的投资,会改变劳动生产效率 \(E\) 和资本生产效率 \(H\),进而影响资本和劳动的投入比例 \(Z/X\)。
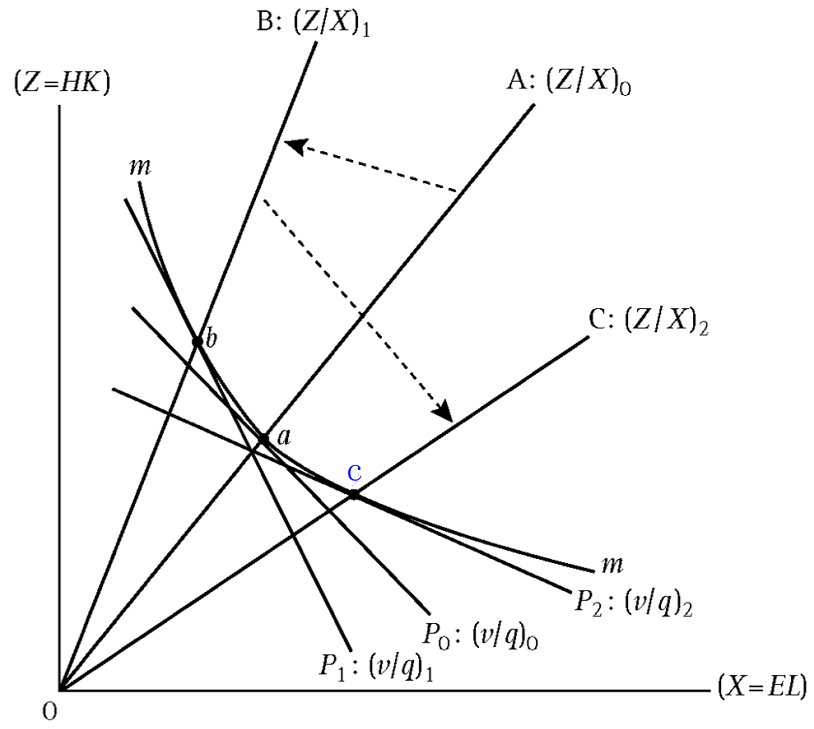
假定在工业化初始期 \(t=0\) 时,要素投入比例为直线 \(OA: (Z/X)_0\),其中,要素投入的相对报酬为 \((v/q)_0\),均衡点为 \(a\) 点。
第一阶段(\(OA \to OB\)):技术进步的倾向是提高资本效率,因此随着资本积累和 \(H\) 的迅速提高,\(Z=HK\) 迅速增长。人力资本投资相对不足,导致 \(E\) 的增长率比 \(H\) 小,即 \(G(E) \lt G(H)\),因此会导致资本利用增加,要素相对投入比例 \(Z/X\) 提高。均衡点发生移动 \(a \to b\),要素相对报酬发生变化 \((v/q)_0 \to (v/q)_1\),此时资本的相对报酬降低,变得更不利于资本投入,但由于资本投入的产出效率更高 \(G(H) \gt G(E)\),因此相对要素价格(工资-利率比率 \(w/r = vE/qH\))保持相对稳定。
第二阶段(\(OB \to OC\)):人力资本投资增加,\(X\) 的增长大大高于 \(H\) 和 \(K\),使得要素投入相对比率 \(Z/X\) 下降。由于 \(E/H\) 的增加补偿了 \(v/q\) 的下降,因此在第二阶段,相对要素价格的比率 \(\frac w r = \frac {E} {H} \cdot \frac {v} {q}\) 上升了。
4. 与一般生产函数的比较
常规生产函数的基本特征是具有非常大的要素替代弹性。
- 若要素替代弹性 \(\sigma \gt 1\),\({ G(Z/X) } \gt { G(v/q) }\),因此在第一阶段,要素投入比例 \(Z/X\) 和要素相对收入份额 \(vZ/qX\) 提高(可能有问题),意味着资本收入份额的增加。
- 若要素替代弹性 \(\sigma \lt 1\),\({ G(Z/X) } \lt { G(v/q) }\),因此在第二阶段,要素投入比例 \(Z/X\) 和要素相对收入份额 \(vZ/qX\) 下降(可能有问题),意味着资本收入份额的下降。
在常规生产函数的假设下,从第一阶段到第二阶段增长类型的变化的理论预期,和利用一般生产函数(ordinary production function)但使科技进步有不同倾向的假设的理论预期是相同的。

