附件：

【附件内容】录屏

【附件下载】链接：https://pan.baidu.com/s/1DVrQZnxCHN48iZTo2RrBqw?pwd=kpmg

主要参考资料：

Athey S, Imbens G W. The state of applied econometrics: Causality and policy evaluation[J]. Journal of Economic perspectives, 2017, 31(2): 3-32.

赵西亮. 基本有用的计量经济学[M]. 北京: 北京大学出版社, 2017.

乔舒亚·安格里斯特, 约恩-斯特芬·皮施克. 基本无害的计量经济学实证研究者指南[M]. 上海: 格致出版社, 2012.

一、识别策略

1. 为何需要因果识别

在理想条件下，对于同一个体，如果能同时观测到实行干预和不实行干预的结果，这两种结果的差异就是这种干预行为的因果效应。然而，现实情况往往是只能观测到一种状态的结果，如果选择干预，就无法观测到未干预的结果，因此无法直接观察到干预行为的因果效应。

为了准确估计干预行为的效果，同时避免潜在结果不可测导致的问题，效仿自然科学的实验研究是一种比较好的选择。在保证干预组与控制组的个体之间几乎无差异的情况下，控制其他的所有因素不变，仅改变某一特定因素，改变该要素的一组是干预组 (treated group)，不改变该要素的一组是控制组 (controlled group)。比较干预组与控制组之间的差别，即可说明这种干预行为的效果。

然而，受制于法律、伦理道德或实验的可行性，用准自然实验的方式进行因果推断往往不具有可行性。绝大多数研究使用观测数据进行因果推断，少数研究也使用准自然实验与观测数据结合的方式进行因果推断。因此，占绝大多数的、基于观测数据开展的研究往往面临上述的仅能观测到一种结果的“因果推断的基本问题” (Holland, 1986)，使用适当的因果识别策略就显得尤为重要。

2. 基本构成要件

潜在结果框架有三个基本构成要件，即潜在结果、稳定性假设与分配机制。

2.1 潜在结果

用$D_i$表示对个体 $i$ 是否实施某种干预行为，当实施干预行为 ($D_i=1$) 时，可以观测潜在结果 $Y_{1i}$；当没有实施干预行为时 ($D_i=0$) ，可以观测到潜在结果。

$\begin {align} Y_i = & D_i Y_{1i} + (1-D_i) Y_{0i} = & \left \{ \begin {array} {lr} Y_i=Y_{1i} , \ \ \ \ if \ \ D_i=1 \\ Y_i=Y_{0i}, \ \ \ \ if \ \ D_i=0 \\ \end {array} \right . \end {align}$

2.2 稳定性假设

稳定性假设 (Stable unit-treatment value assumption, SUTVA) 要求干预行为对个体的影响是稳定的。具体来看主要包括以下两个方面：

第一，个体之间的潜在结果没有相互影响，每个个体的潜在结果相互独立。这避免了干预行为或非干预行为的外溢对潜在结果估计的扭曲。

第二，对每个干预组个体要实行相同的干预性为。例如讨论培训对收入的影响，将多种不同的培训均视作干预行为，严格意义上不满足该条件。

2.3 分配机制

分配机制对因果效应的估计也十分重要。分配机制解决什么样本应当进入干预组，什么样本应当进入控制组。

由于存在无法同时观测干预与不干预行为的潜在结果，在考虑分配机制问题时，应当要考虑不受干预行为影响的两类因素：

个体属性：不随干预状态变化而变化的因素，以年龄等个人特征最为常见
干预的前定因素：发生在干预性为之前的相关协变量，例如干预性为之前的收入等

在基于随机化实验开展的研究中，分配机制是明确的；但在基于观测数据开展的研究中，干预组与控制组往往并非由研究人员分配，分配机制是未知的，此时进行因果识别的重要问题就是识别出未知的分配机制。

非混杂性假设 (Unconfoundedness Assumption) 表示所有可能影响到潜在结果的因素都可以被观测到，不存在不可观测的混在因素对潜在结果的估计产生影响，即：

$\begin {align} (Y_{0i},Y_{1i}) \perp D_i \ | \ X_i \end {align}$

也就是说，在控制协变量 $X_i$ 后，干预行为与潜在结果独立。

因此，分配机制可以分为三类：

已知分配机制，且满足非混杂性假设：随机化实验
未知分配机制，且满足非混杂性假设：规则分配机制 (例如 PSM)
其他情况：不规则机制

二、随机化实验与回归法

1. 随机化实验

在随机化实验中，样本被随机分配到干预组与控制组，因此分配机制不依赖于潜在结果，满足非混杂性假设。

$\begin {align} (Y_{0i},Y_{1i}) \perp D_i \end {align}$

因此，随机化实验中，干预组与控制组的观测结果之差即可解释为因果效应。

随机化实验可以分为四类：

伯努利实验 (Bernoulli Trials)
完全随机化实验 (completely randomized experiments)
分层随机实验 (stratified randomized experiments)
配对随机化实验 (paried randomized experiments)

伯努利实验在同样的条件下重复地、相互独立地进行随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。

但是伯努利实验有可能出现所有样本均在干预组或控制组中，导致无法通过比较干预组与控制组进行因果推断。

完全随机实验要求事先设定干预组个体数量 $N_t$，剩下的 $N-N_t$ 进入控制组。

分层随机实验则在完全随机实验的基础上，依据某些对潜在结果影响较大的因素进行分层，在层内实行完全随机化实验。

配对随机化实验是一种特殊的分层随机化实验，将所有个体分成 $N /2$ 组，每一组只有两个个体，且一个在干预组，一个在控制组。

在分层随机化实验中，也要求非混杂性假设或条件独立性假设 CIA 成立，即 $(Y_{0i},Y_{1i}) \perp D_i \ | \ X_i$。

由于随机化实验要求所有个体被随机分配到干预组与控制组，干预状态不是个体选择的结果，随机化实验的结构解释为总体的平均因果效应。然而在现实中，干预行为往往与个体选择有关，使用随机化实验得到的结果并不一定是现实中干预行为的因果效应。

2. 回归法

回归分析本质是相关性分析，而非因果效应的估计。因此，基于观测数据使用回归法进行因果效应估计时，需要满足一定的条件。

在随机化实验中，干预组与控制组的潜在结果差异即为因果效应。然而，在满足稳定性假设的条件下，使用随机抽样的观测数据进行因果效应识别时，由于处理效应 $Y_{1i}-Y_{0i}$ 是一个随机变量，我们一般更加关注平均因果效应。

平均处理效应 ATE (Average Treatment Effect)
平均处理效应 ATT / ATET (Average Treatment Effect on Treated)

$\begin{align} ATE & \equiv E(Y_{1i}-Y_{0i}) \\ ATT & \equiv E(Y_{1i}-Y_{0i} \ | \ D_i=1) \end {align}$

因此，有如下关系：

$\begin {align} E(Y_{1i} \ | \ D_i=1) & - E(Y_{0i} \ | \ D_i=0) = \notag \\ & [ E(Y_{1i} \ | \ D_i=1) -E(Y_{0i} \ | \ D_i=1) ] + [ E(Y_{0i} \ | \ D_i=1) -E(Y_{0i} \ | \ D_i=0) ] \end{align}$

其中：等式左边为 ATE，右边第一项为 ATT，第二项为选择偏差。

对于二元的处理变量，使用基于极大似然法的 probit 与 logit 模型 (非线性概率模型)，可以克服线性概率模型的拟合的结果可能不在 [0,1] 之间的问题。

使用线性回归进行因果效应估计时，必须满足以下两个条件同时成立。

$\begin {align} E(Y_{0i} \ | \ D_i=1) = E(Y_{0i} \ | \ D_i=0) \\ E(Y_{1i} \ | \ D_i=1) = E(Y_{1i} \ | \ D_i=0) \end {align}$

三、匹配法

倾向得分匹配主要用于解决未知分配机制的问题，当满足非混杂性假设时，使用 PSM 可以准确识别因果效应。但当不满足非混杂性假设，即存在不可观测变量的影响时，使用 PSM 不能消除不可观测变量的影响，估计结果是受到扭曲的因果效应。

1. 前提假设

使用匹配法进行因果识别，应当满足以下几个条件：

条件独立性假设 CIA：$(Y_{0i},Y_{1i}) \perp D_i \ | \ X_i$
共同区间假设 (Common Support)：$0<Pr(D_i =1)<1$，即倾向得分的取值在0~1之间

2. 估计步骤

匹配方法的估计包括四个步骤：

定义相似性
实施匹配
评价匹配效果
估计因果效应

2.1 定义相似性

相似性的定义包括了两个环节：

选择协变量：协变量的选择应当满足条件独立性假设，干预组与控制组之间没有未观测到的差异。
- 遗漏变量可能会造估计结果的偏差
- 添加与干预变量无关的变量不会影响估计结果
测度相似性：通常使用欧氏距离或马氏距离衡量

在倾向得分匹配中，常使用平衡性检验检查干预组和控制组的协变量均值差异，以检验条件均值独立性假设是否成立 (条件独立性假设难以验证，检验条件均值独立性假设是否成立是一种证伪检验)。

2.2 实施匹配

匹配的方式分为：

近邻匹配
- 一对一匹配
- 一对多匹配：半径匹配、马氏匹配等
分层匹配
核匹配

2.3 评价匹配效果

标准化平均值差异
对数标准差比
倾向指数的标准化平均值差异
图示：倾向得分分布图、分位数分布图、标准化平均值差异变化图

2.4 估计因果效应

对于不同的匹配方式，估计因果效应的方法不同。

四、工具变量法

如上文所述，在因果效应识别时，应当满足无混杂性假设。然而在现实中，无混杂性假设很难被满足。例如在探究教育年限 $D$ 对收入 $Y$ 的影响时，学生的能力 $A$ 可能是一种混杂因素，即学生的能力越强，其接受教育的年限可能越高，同时收入也可能会越大。传统 PSM 法估计无法解决学生能力等内部混杂因素与政策环境等外部混杂因素对因果识别结果的扭曲，这也是工具变量法区别于 PSM 的关键。

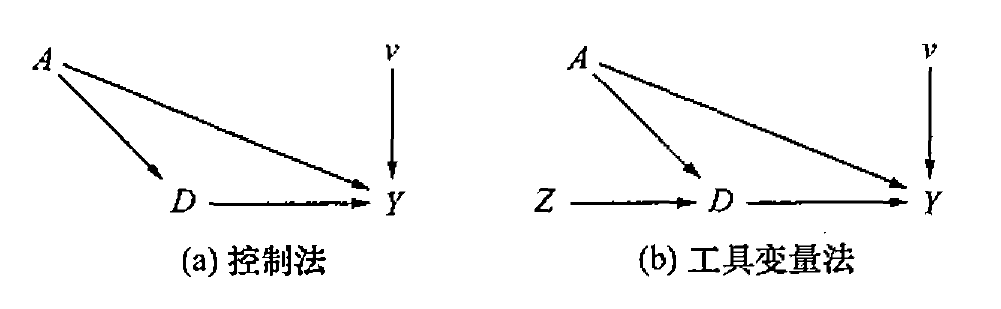
工具变量法的有相无环图

在工具变量法 (右图 b) 中，有向无环图如下所示，如果存在一个工具变量 $Z$ 满足相关性与外生性的条件，就可以消除混杂因素 $A$ 对结果的扭曲。

相关性：$Cov(D_i, Z_i) \ne 0$，即工具变量 $Z$ 与核心解释变量 $D$ 相关
外生性：$Cov(\eta_i, Z_i) = 0$，即工具变量与 $Z$ 与包含混杂因素 $A$ 的残差项 $\eta$ 不相关，其中 $\eta_i = A^{‘}_i \gamma +v_i$。( 工具变量的外部有效性 )

工具变量可以消除混杂因素影响的原理是：

阻断后门路径 $D \leftarrow A \rightarrow Y$，从其中分离出 $D \rightarrow Y$。

在实证中，为保证因果效应被准确识别，如果存在 $m$ 个混杂因素，应当需要不少于 $m$ 个工具变量。

五、固定效应、双重差分与合成控制

上述的回归法、匹配法是基于截面数据，其正确估计因果效应的基础都是要满足非混杂性假设 / 条件独立性假设。但观测数据往往不能涵盖所有的可能影响因素，当存在混杂因素影响时，条件独立性假设不再被满足，可以使用工具变量法，基于阻断后门路径的方式实现因果推断。但工具变量往往很难寻找，且存在一定的工具变量滥用问题。

在面板数据与重复截面数据中，固定效应、双重差分与合成控制等方式可用于因果效应的识别。

1. 固定效应法

使用固定效应法估计因果效应，应当满足面板数据下的条件独立性假设：

$\begin {align} (Y_{1it},Y_{0it}) \perp D_{it} \ | \ X_{it} , \ U_i, \ t \end{align}$

如上所示，$X_{it}$ 表示可观测得混杂因素；$U_{it}$ 表示不随时间变化的不可观测混杂因素，$t$ 表示时间。

因此，当满足上述条件后，所有随时间变化的混杂因素都可以被观测，通过控制可观测的混杂因素，就可以消除混杂因素对因果效应估计结果的扭曲，得到总体干预组的平均因果效应 ATT。不随时间变化的混杂因素的影响 (即固定效应) 可以通过均值法或差分法消除。

固定效应中涉及的差分法，是干预行为的“事前”与“事后”的差分。

2. 双重差分法

固定效应法可以消除不随时间变化的混杂因素影响，然而当结果变量发生了结构性变化，例如 2008 年的次贷危机，导致次贷危机发生前与发生后中国的经济结构发生了很大变化。此时，若仅满足固定效应法的条件独立性假设，不能克服结构性变化带来的影响。

考虑到在时间维度上，控制组可能也受到相同因素的影响，干预组与控制组可能发生类似的结构性变化，因此，通过双重差分的方式，即可控制这种结构性变化带来的影响。

双重差分：“事前”与“事后”的差分，干预组与控制组的差分。

2.1 基本假设：

共同趋势假设：干预组与控制组受到相同变动趋势的影响
共同区间假设：$Pr(D_i =1) \gt 0$且 $Pr(D_iT_t=1 \ | \ X_{it})<1$，即总体中同时存在干预组与控制组个体
外生性假设：$X_{1it}=X_{0it}=X_{it}$ ，即协变量外生于干预政策。因此，协变量 $X_{1it}$应该是发生在政策干预实施之前 (前定变量) 或者不随干预政策发生变化的变量
SUVTA：干预政策只影响干预组，不会对控制组产生影响，这保证了干预政策没有溢出效应。

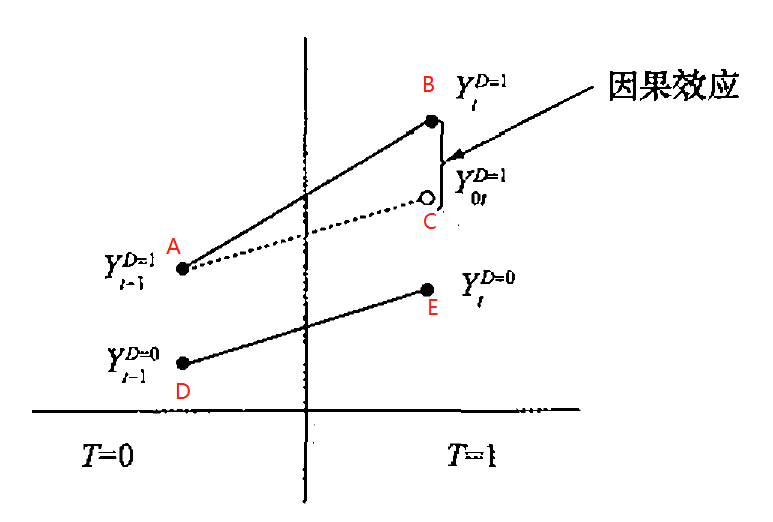
图示：

$AC \parallel DE$：即为满足共同趋势假设
$AC$ 与 $DE$ 的距离即为干预组与控制组的差距；
$BC$ 即为因果效应。

2.2 检验

2.2.1 平行趋势检验

在实际研究中，进行 DID 回归，一般要进行平行趋势检验，例如，在 Zhu et al. 的 Removing the "Hats of Poverty": Effects of ending the national poverty county program on fiscal expenditures 一文中，使用了多种方式进行平行趋势检验：

使用数据的均值走向图，试图论证在政策实施前，试点与非试点地区的经济情况具有平行关系。

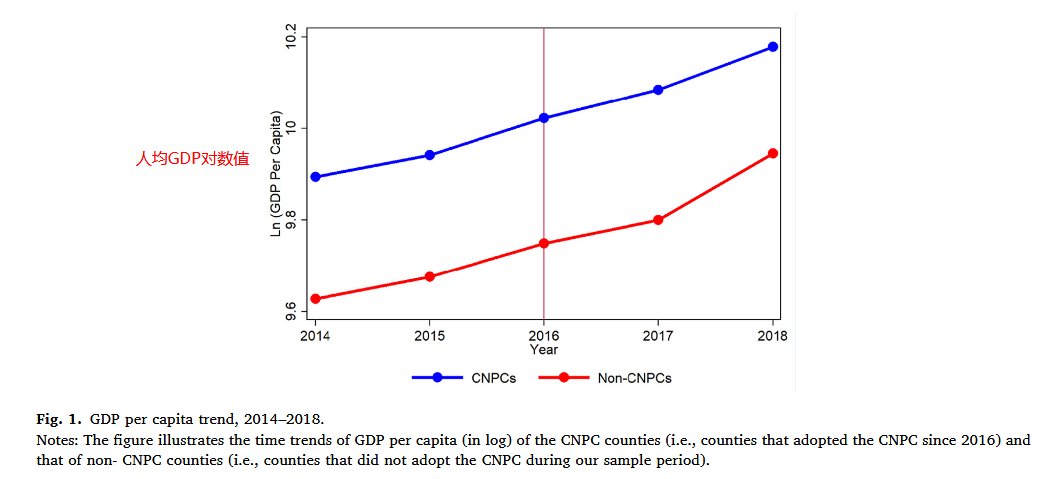
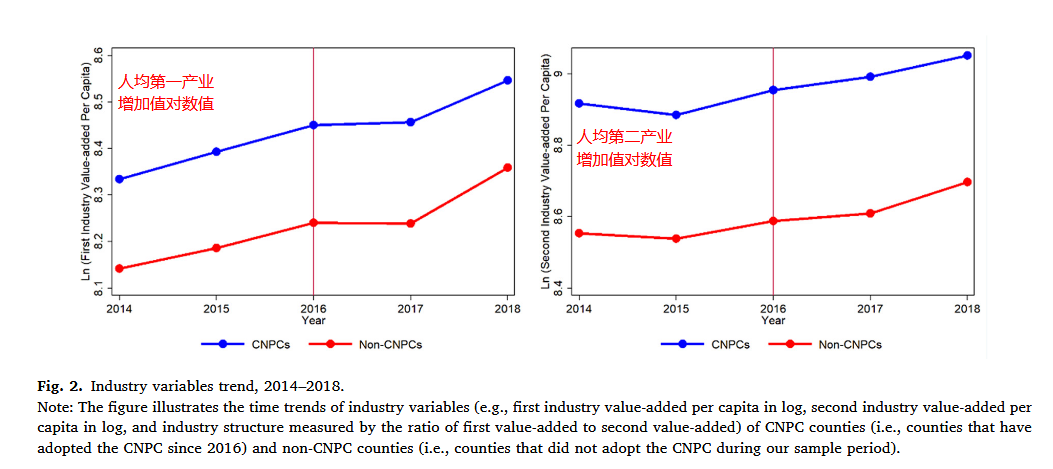
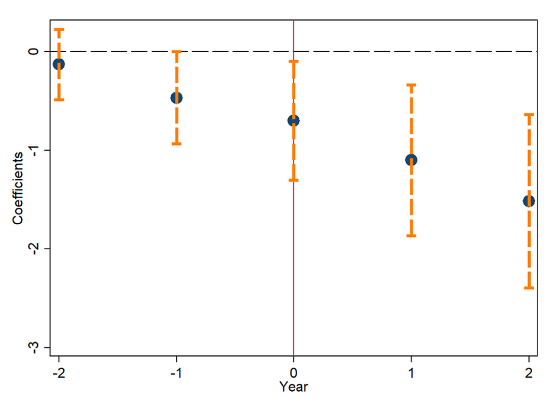
对面板数据进行逐年回归，通过回归系数的大小与显著性比较论证平行趋势的存在。

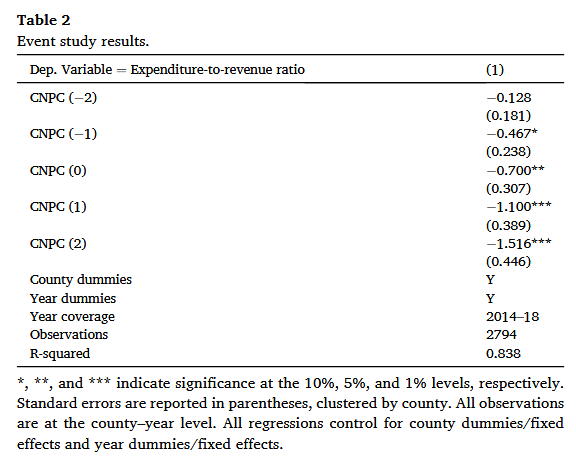
通过事件研究法的结果图示展现平行趋势，在政策执行前，回归系数的置信区间包含0；政策执行后，回归系数的置信区间不再包含0。

2.2.2 安慰剂检验

安慰剂检验主要包括两种方法，一是更改政策干预时间，二是构造伪样本组。例如，将政策干预时间设定为实际干预前的$t-2$期，如果系数不显著，可以认为将$t-2$期设定为政策干预时间是不合适的；反之，如果系数显著，可以认为基准回归的显著结果可能是其他政策或者非政策的外部环境变化带来的。

一些学者也通过置换检验的方式 (permutation test)，对 DID 进行了安慰剂检验，例如，石大千等发表于《中国工业经济》的《智慧城市建设能否降低环境污染》，随机抽取控制组中的部分样本作为“伪干预组”，用于证伪“假干预”行为没有政策效果。

3. 合成控制法

干预组与控制组之间的相似度足够高，是使用双重差分法保证平行趋势的重要条件。当控制组与干预组中的个体都不相似时，可以对多个控制组个体赋予不同的权重，计算加权平均值，构造出一个合成的控制组，这使得合成控制组与干预组在发生干预行为之前的状态非常相似。干预组与合成控制组的差异即为因果效应。

特点：干预组个体往往只有一个，例如一个城市、地区或者国家

3.1 基本假设：

干预组与控制组无交互影响
构造合成控制组时，两组个体的协变量必须是前定变量或不受政策干预影响的变量
各控制组的权重非负，且和为 1

3.2 例子

以 Abadie et al. (2010) 的加州香烟控制项目对香烟消费的影响为例，1988 年 11 月，加州政府通过了香烟控制项目，每包烟的消费税提高 25 美分，于 1989 年 1 月开始生效。作者将加州作为干预组，将美国未出台香烟管控政策的 38 个州作为控制组，考察消费税增加对年度人均香烟消费量的影响。

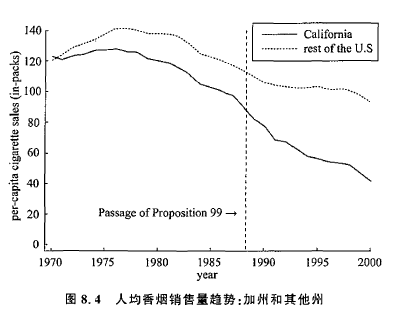
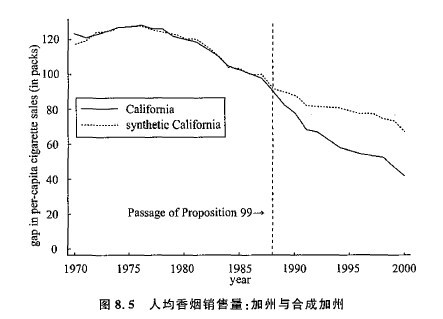
可以发现，通过合成控制法，可以实现未实施政策干预时干预组与合成控制组基本重合，若不实行香烟管控政策，加州的变化趋势应当与合成控制组的曲线完全重合。但实施了香烟管控政策的加州，人均香烟消费量明显更低，与合成加州有明显的差距，这表明改政策具有明显的降低香烟消费的效果，且随着时间的推移下降效果更加明显。

3.3 检验

类似于 DID，合成控制法也需要进行平行趋势检验与安慰剂检验。

在合成控制法中，平行趋势关系已在图中展示，因此不需要额外检验。

安慰剂检验方法：

置换检验：在控制组中抽取样本作为“假干预组”
伪干预时间：更改干预时间，检验是否在真实的干预时间处有政策效果，或在当前伪干预时间处没有政策效果。

4. 回归合成控制法

合成控制法要求控制组个体的权重为非负，且和为 1。在此条件下可能无法构造出与干预组非常相似的合成控制组。

因此回归合成法放宽了该条件。回归合成控制法利用截面个体之间的相关性进行干预组个体受政策干预后的反事实结果，并允许群众某个控制组个体的权重为负，并且允许存在常数项，以修正合成控制组和干预组之间的差异。

回归合成控制法中，控制组的选择影响了估计精度。进入模型的控制组个体越多，模型自由度损失越多，精度越差。

例子：

萧政 (Hsiao et al., 2012) 考察 1997 年香港回归与 2003 年签署的《内地与香港关于建设更紧密经贸关系的安排》(CEPA) 对香港经济的影响。

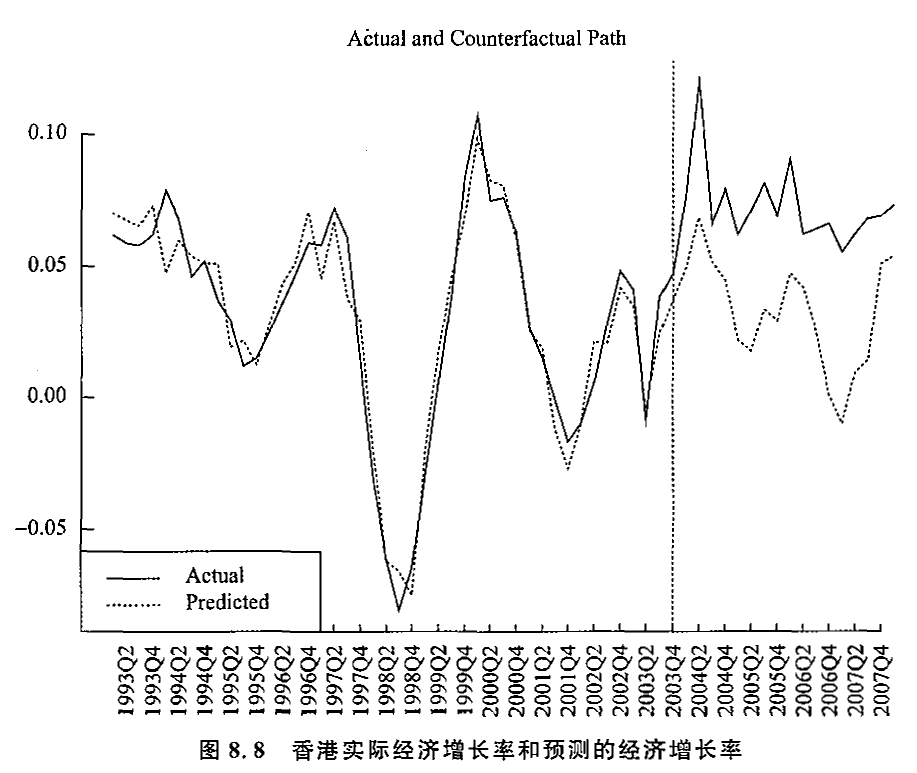
通过回归合成控制法，可以发现 1997 年香港回归没有显著影响香港经济，而 CEPA 对香港经济有显著的促进作用。

六、断点回归

参考：RD Packages - Regression Discontinuity Designs (Calonico et al.)

1. 适用条件与假设

1.1 使用条件

可观测的配置变量 (forcing variable): 用于断点识别的外生变量，例如生日、年龄、分数、地理位置等（原文链接）。
配置变量在某一阈值附近的变化，会使得处理变量的取值发生不连续变化，配置变量取值在阈值一侧的样本为干预组，另一组则为控制组。

1.2 假设

断点假设：个体分配的概率在临界值附近有跳跃，即断点存在
连续性假设：除临界值附近外，控制了协变量的潜在结果期望值连续变化，即在断点附近，估计潜在结果时协变量的影响可以忽略不记。(类比 PSM 平衡性检验)
局部随机化假设：在临界值附近，配置变量 $X$ 的取值应当近似于随机化实验，不受到其他不可测因素 $U$ 的影响，不存在 $U\rightarrow X$ 的影响路径，因此配置变量 $X$ 可以作为判断样本是否受到干预 $D$ 的依据。也就是说，在实证中需要满足 $X$ 是严格外生的条件。
独立性假设：决定干预组与控制组的断点严格外生，不会与潜在结果或个人因素相互影响。
单调性假设：断点对所有个体的影响方向相同，即若正向单调性成立，则 $D_{1i}>D_{0i}$。

2. 类型

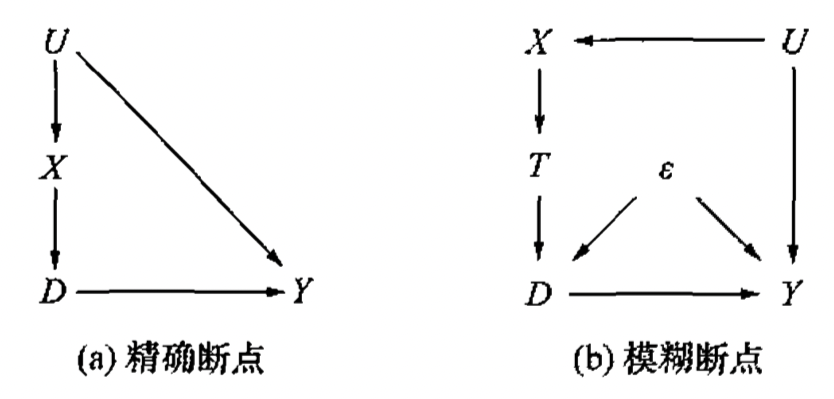
RDD 因果图

精确断点 (Sharp RDD)：在断点 $D=c$ 处，个体的受干预概率从 0 跳跃为 1；
模糊断点 (Fuzzy RDD)：在断点 $D=c$ 处，个体的受干预概率从 $a$ 跳跃为 $b$，且 $0<a<b<1$
弯折回归设计 (Regression Kink Design): 当二元的处理变量在断点处不是间断性跳跃，而是弯折时，在满足平滑性假设下，可以使用弯折识别因果效应。

与匹配法的异同点：

条件独立性假设 CIA 仍然成立，$(Y_{0i},Y_{1i}) \perp D_i \ | \ X_i$，即在控制协变量 $X_i$ 后，处理变量不影响潜在结果。
共同区间假设不再成立，因为当配置变量取值超过阈值时，所有样本都会被进入干预组，受到干预行为的概率是 $1$，而不再是在 $(0,1)$ 区间内。

在上述条件下，使用回归法或者匹配法估计的因果效应是不准确的。

3. 使用断点回归的四个关键点：

使用局部线性估计 (Porter, 2003)，以纠正在临界值附近数据跳跃发生的系统性变化
带宽的选择问题：估计精度(估计方差) 与估计偏差的权衡问题
- 干预行为的影响是异质性的，由于单调性假设，离断点越远的点，与断点处的异质性越强。
  - 若带宽较大，估计精度会提高，但样本相似度降低，估计偏差会增大
  - 若带宽较小，估计精度会降低，样本相似度会提高，估计偏差会减小
- 局部线性回归的带宽建议使用估计量在带宽极小值附近的渐进扩展 (IK 最优带宽和 CCT 最优带宽)
模型设定检验
- 伪断点检测：将配置变量其他取值作为临界点，检验其他断点的处理效应是否为 0。如果不为 0，则 RDD 可能有问题，断点结果可能是不可观测因素的混杂效应导致的
- 配置变量的不连续性检测：如果断点处配置变量分布是连续的，说明配置变量临界值处的个体没有操纵参考变量的能力。
- 带宽选择的敏感性检验。如果带宽的选择对结果的影响较大，则 RDD 可能有问题
- 协变量连续性检验 / 伪结果检验：以协变量作为伪结果，检测 RDD 估计量是否显著，如果显著，说明协变量不满足连续性假设。(类比 PSM 平衡性检验)
在不同的子样本中检验结果

4. 例子

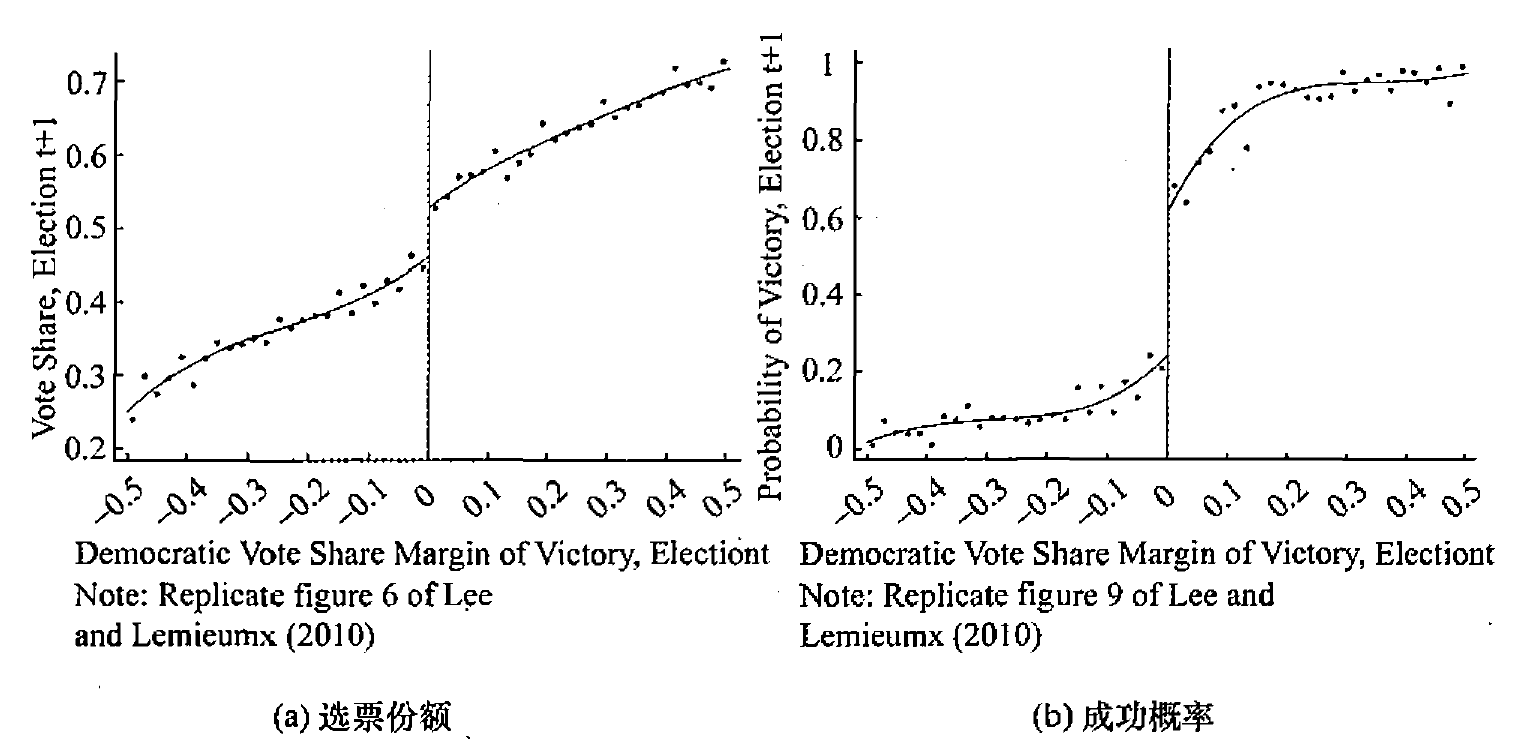
研究美国某一党派在上次胜选后，是否会影响下一次胜选的概率。

选票份额差距为 0 即为断点，断点右侧，民主党选票超过了 50%，与断点左侧民主党选票低于 50% 有明显断点。若民主党上一次胜选 (图 a 断点右侧)，本次选举胜选的可能性会更高 (图 b 断点右侧)。

5. 检验

在断点回归中，更换断点 (配置变量临界值) 是进行安慰剂检验的方式之一。

断点回归的关键识别条件是个体不能精确控制临界点。如果个体可以操纵临界点，可能使断点左右个体分布差异很大，因此可以使用绘制配置变量分布图的方式检验配置变量的独立性问题。

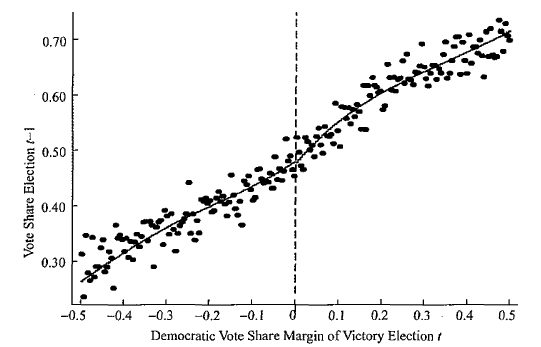
例如，前一期民主党选票的份额和配置变量的关系图 (上图) 中，临界点处没有发生明显跳跃，说明上一期民主党选票份额这一协变量不会影响配置变量的取值。

七、其他方法

1. 多值处理变量的因果效应估计

上述内容主要针对二分类的处理变量，满足稳定性假设。然而，许多干预行为并不仅是“是否受到干预”的问题，还有干预强度的差异。

最常见的解决这类问题的方法是使用广义倾向得分法来解决多值离散变量或连续变量的干预因果效应问题。

广义倾向得分法的相关研究主要针对截面数据中非二值处理变量的因果效应问题。以 Barbara et al. (2014) 基于 Hirano and Imbens (2004) 开发的 glmdose 命令为例，其基本思路是：

平衡性检验：基于干预强度变量取值，划分多层样本，并比较层内干预组与控制组的协变量均值差异；
计算广义倾向得分 (GPS)：满足平衡性检验以后，基于协变量估计处理强度的条件概率密度
构造条件期望：基于干预变量与 GPS 值计算潜在产出的条件期望模型
设置估计精度：用户设置估计干预变量的步长，用户控制估计精度
剂量反应函数：基于构造潜在产出的条件期望模型与设置的步长，估计剂量反应函数，并绘制剂量反应函数图。

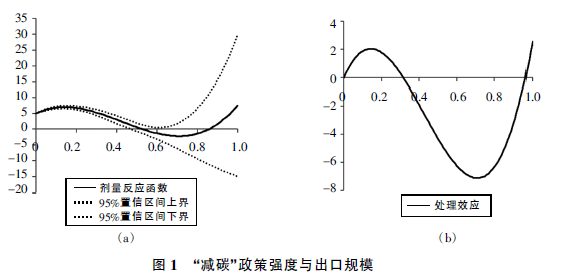
图片来源：《“减碳”政策制约了中国企业出口吗》《中国工业经济》

由此可见，GPSM 法与传统 PSM 法之间存在关联与区别：

关联：
- 在每一组内，协变量需要满足非混杂性假设
- 基于协变量的取值计算倾向得分，并作为匹配的依据
区别：
- 倾向得分的计算方式不同
- 组内匹配的方式也有所不同
- 需要用户设置步长，以确定估计的精度水平
- 结果不再关注干预组与控制组之间的平均处理效应，而是剂量反应函数的变化趋势

但是，在使用该类方法进行因果推断时，仍然面临一个问题：当时用面板数据考察连续变量的干预效果时，仍然将其当做截面数据进行估计，丧失了面板数据存在时间趋势与固定效应进而可以消除不随时间变化的不可观测因素影响的优势。例如，《中国工业经济》中曾刊载《“减碳”政策制约了中国企业出口吗》一文，使用 doseresponse2 命令 (glmdose 命令的前身) 估计面板数据中连续处理变量的因果效应。

2. 社会网络中的因果效应识别

在社会学的相关研究中，“同侪效应”是因果效应识别的重要问题。即某人的受干预行为会因模仿等原因受到身边同类型人群（如同龄人）受干预行为的影响，这导致在因果识别问题中的稳定性假设 SUTVA 这一基本假设不再成立。

Manski (1993) 提出同侪效应包括三种：

关联同侪效应
外生同侪效应
内生同侪效应

这三种效应的识别依赖很强的假设，且部分假设难以符合现实。

3. 机器学习

‍机器学习在因果推断中的应用，主要有三种方法：

双重选择程序 (Belloni et al., 2013)
- 使用LASSO回归选择与结果相关的协变量
- 选择与干预变量相关的协变尽量
- 选取上述两组协变量的并集，并带入OLS
模拟随机试验 (Hainmueller, 2012; Graham et al., 2012 & 2016)
- 重新计算干预组与对照组的平衡协变量或协变量函数的权重
半参数估计 (van der Vaart, 2000)
- 离散型处理变量——使用潜在结果的期望产出 (平均值)
- 连续性处理变量——使用非参数估计

在上面的论述中，多数因果识别方法都是基于稳定性假设，即干预行为对干预组的影响是相同的。然而，在不同的环境中，一种干预行为的效果可能并不相同。在估计异质性的因果效应时，使用机器学习的方法可能有助于解决上述问题，例如因果树 (causal trees)、BART (Bayesian Additive Regression Trees)。