微观|第10章:博弈论
【内容速查与目录】
【笔记下载】
一、博弈论和策略行为
博弈论(game theory)是研究在策略性环境中如何进行策略性决策和采取策略性行动的科学。
博弈的三个基本要素:
- 参与人
- 参与人的策略
- 参与人的支付
博弈的分类:
- 根据参与人的数量:二人博弈、多人博弈;
- 根据参与人拥有的策略的数量:有限博弈、无限博弈;
- 根据参与人的支付情况:零和博弈、非零和博弈;
- 根据参与人是否能够达成有效的协议:合作博弈、非合作博弈;
- 根据参与人是否了解有关博弈的所有信息:完全信息博弈、不完全信息博弈;
- 根据参与人在策略的实施上是否具有“同时性”:静态博弈(或同时博弈)、动态博弈(或序贯博弈)。
二、完全信息静态博弈:纯策略均衡
(一)支付矩阵
二人同时博弈可以用支付矩阵来描述和分析,如下表所示。

(二)条件策略和条件策略组合
把甲厂商在乙厂商选择策略条件下的最优策略称为甲厂商的条件策略;把与甲厂商的条件策略相联系的策略组合称为甲厂商的条件策略组合。
(三)纳什均衡
1. 概念
纳什均衡,指的是参与人的这样一种策略组合。在该策略组合上,任何参与人单独改变策略都不会得到好处。如果在一个策略组合中,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡。
在纳什均衡的定义中,有两个问题需要注意:
- “单独改变策略”是指任何一个参与人在所有其他人都不改变策略的情况下改变自己的策略。
- “不会得到好处”是指任何一个参与人在单独改变策略之后自己的支付不会增加。
2. 纳什均衡的确定(条件策略下划线法)
- 把整个博弈的支付矩阵分解为两个参与人的支付矩阵。
- 在第一个(即位于整个博弈矩阵左方的)参与人的支付矩阵中,找出每一列的最大者,并在其下划线。
- 在第二个(即位于整个博弈矩阵上方的)参与人的支付矩阵中,找出每一行的最大者,并在其下划线。
- 将已经划好线的两个参与人的支付矩阵再合并起来,得到带有下划线的整个博弈的支付矩阵。
- 在带有下划线的整个的支付矩阵中,找到两个数字之下均划有线的支付组合。由该支付组合代表的策略组合就是博弈的纳什均衡。

利用下划线法得出,纳什均衡是(不合作,不合作)。
3. 纳什均衡的存在性、唯一性、稳定性和最优性
3.1 存在性
在完全信息的静态博弈中,(纯策略的)纳什均衡既可能存在,也可能不存在。

3.2 唯一性
在完全信息的静态博弈中,如果纳什均衡存在,既可能是唯一的,也可能是不唯一的。

3.3 稳定性
在完全信息的静态博弈中,如果纳什均衡存在,既可能是稳定的,也可能是不稳定的。

3.4 最优性
在完全信息的静态博弈中,如果纳什均衡存在,既可能是最优的,也可能不是最优的。

4. 纳什均衡和社会福利
4.1 囚徒困境模型
通过分析可以看出,张三和李四的决策都是坦白。但是,如果两人都选择不坦白,则都可以获得最好的结局。很清楚,囚徒困境反映了一个矛盾:即个人理性和团体理性的冲突。

4.2 广告大战

纳什均衡(做广告,做广告)不仅对参与人不是最优的,且对整个社会也不是最优的。
三、完全信息静态博弈:混合策略均衡
即使纯策略的纳什均衡不存在,相应的混合策略纳什均衡却总会存在。

和纯策略组合不同,混合策略组合是一个概率向量组合,每一个概率向量是相应参与人的一个混合策略。
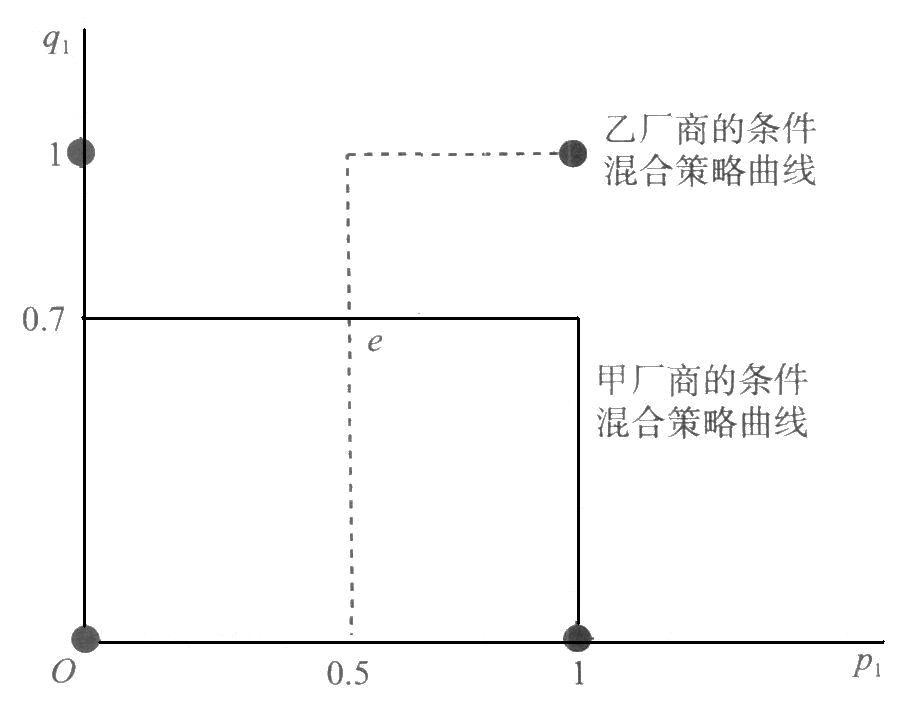
甲厂商的期望支付为:\(E_甲=p_1(7-10q_1)+5q_1+2\),那么甲厂商条件混合策略为:
\[ x = \left \{ \begin {align} & 1 & if \ \ q_1 \lt 0.7 \notag \\ & [0,1] & if \ \ q_1=0.7 \notag \\ & 0 &if \ \ q_1\gt 0.7 \notag \\ \end {align} \right. \]
乙厂商的期望支付为:\(E_乙=5p_1(2q_1-1)-7q_1+8\),那么乙厂商条件混合策略为:
\[ x = \left \{ \begin {align} & 1 & if \ \ q_1 \lt 0.5 \notag \\ & [0,1] & if \ \ q_1=0.5 \notag \\ & 0 &if \ \ q_1\gt 0.5 \notag \\ \end {align} \right. \]
借用条件混合策略可确定混合策略的纳什均衡。
四、完全信息动态博弈
在完全信息动态博弈中,参与人的决策有先有后,特别是,后行动的参与人可以观察到先行动的参与人已经采取了的策略。
(一)博弈树
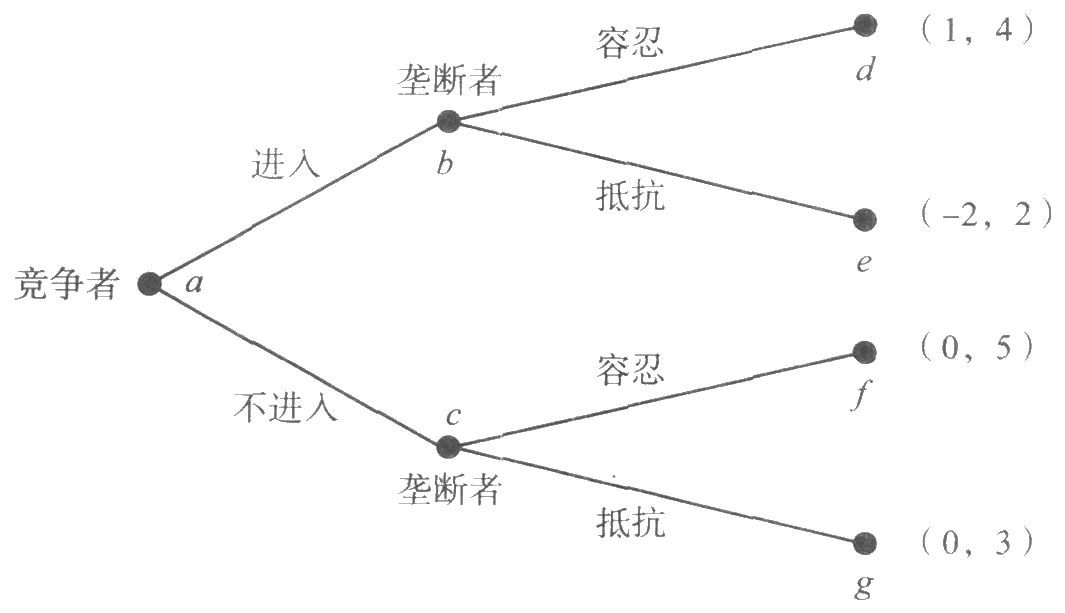
例子:竞争者—垄断者博弈
描述序贯博弈的工具是“博弈树”,由“点”(包括“起点”“中间点”“终点”)、连接点的“线段”以及标在这些点和线段旁边的文字和数字组成。
以博弈树来描述的完全信息的动态博弈称为扩展型博弈。
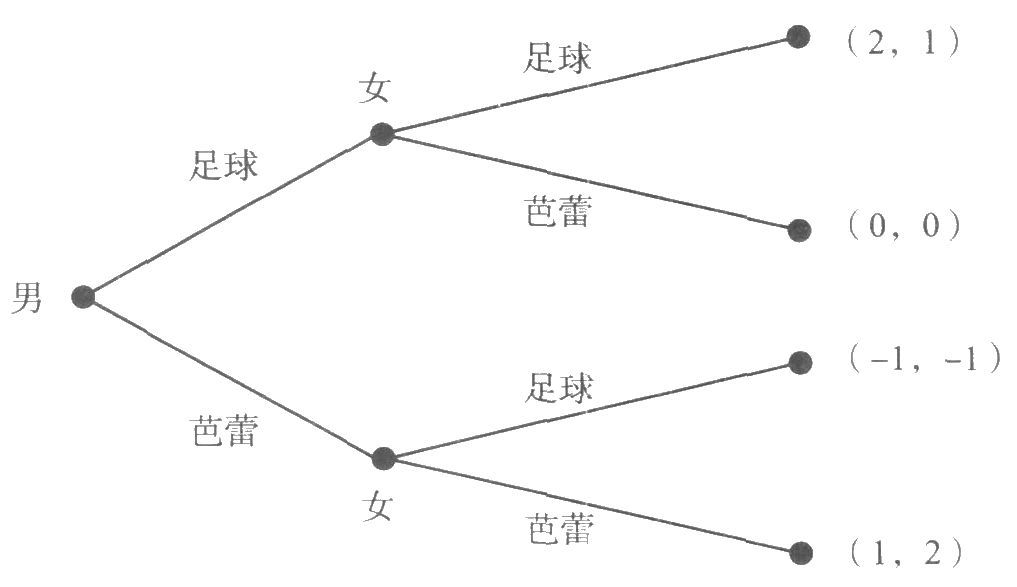
(二)纳什均衡的求解
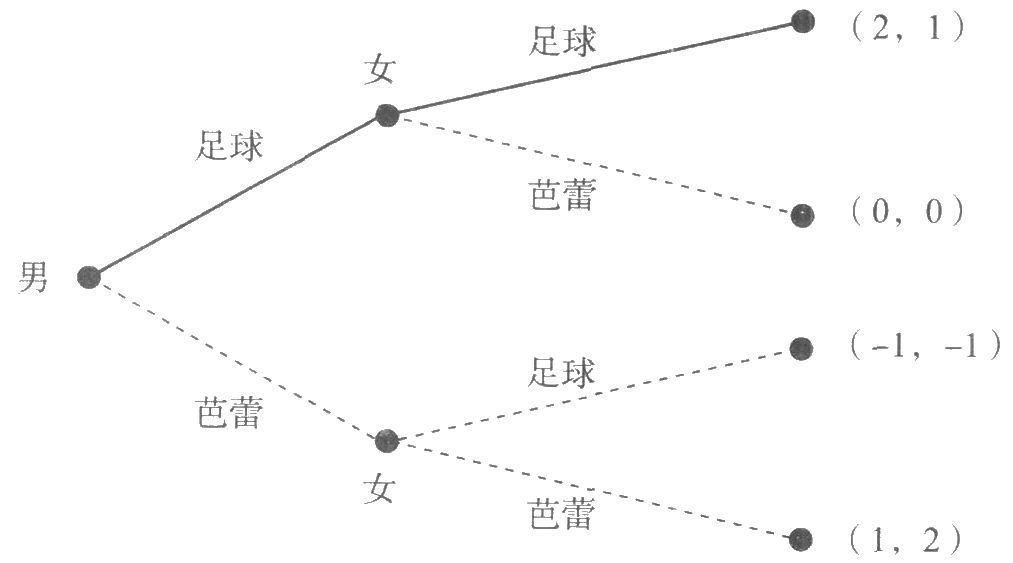
竞争者—垄断者博弈中,纳什均衡为(进入,容忍)。如下图博弈中,两个纳什均衡:(足球,足球)、(芭蕾、芭蕾)。
(三)纳什均衡的精炼:逆向归纳法
1. 逆向归纳法
对纳什均衡的“精炼”,即从众多的纳什均衡中进一步确定“更好”的纳什均衡。纳什均衡的精炼方法通常是使用“逆向归纳法”。
(1)先从博弈的最后阶段的每一个决策点开始,确定相应参与人此时所选择的策略,并把参与人所放弃的其他策略删除,从而得到原博弈的一个简化博弈。
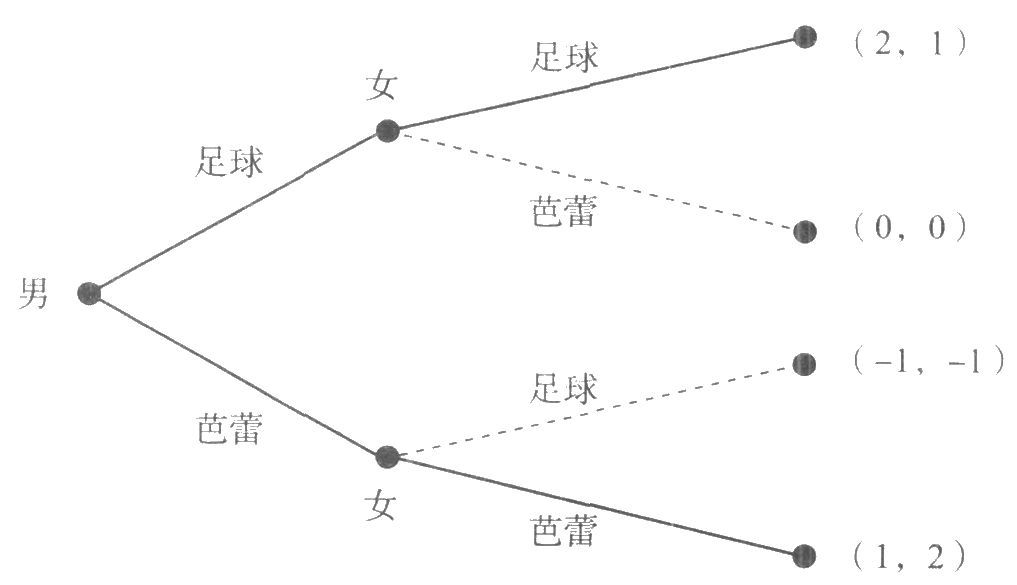
(2)再对简化博弈重复步骤一的程序,直到最后,得到原博弈的一个最简博弈。这个最简博弈就是原博弈的解;而在存在多重纳什均衡时,它就是对纳什均衡的精炼。
2. 精炼的纳什均衡与效率
对参与人来说,由逆向归纳法“精炼”出来的完全信息动态博弈的纳什均衡也不一定是有效率的。
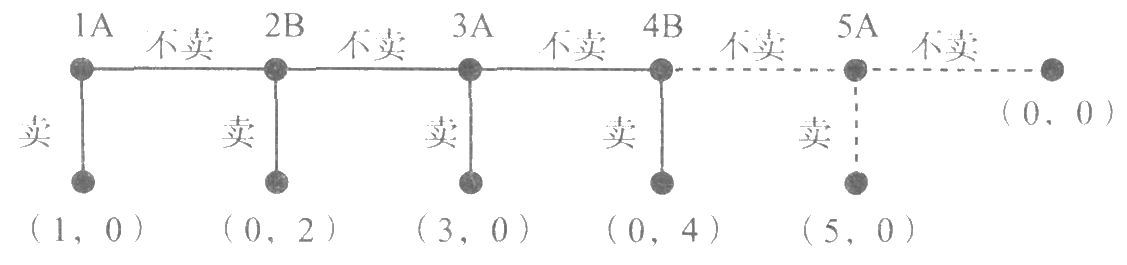
该博弈在一开始时就会以 A 决定卖而结束,相应的支付组合为(1,0),即 A 得到净收益 1,B 得到净收益 0。
相关资源:

