发展经济学|附录A6-要素份额变化的数学分析
⚠️ 注意:本节的分析可能有误!
使用下图来解释要素份额变化的机制,其中曲线 \(m\) 表示等产量线。
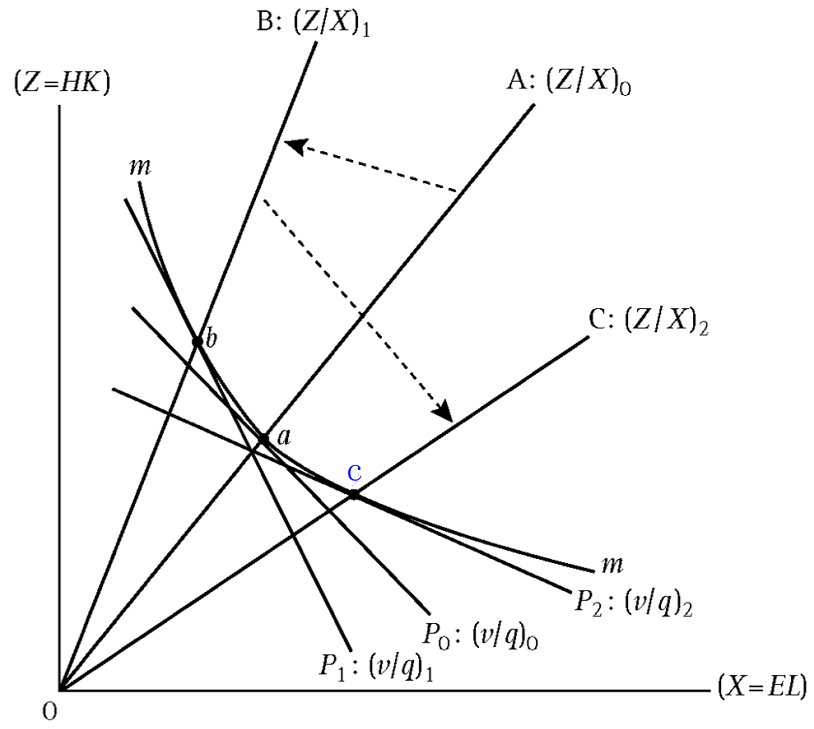
假定产出 \(Y\) 由两种要素生产出来:质量调整后的劳动力 \(X=EL\),质量调整后的资本投入 \(Z=HK\)。两种生产要素都使边际效率衡量:
\[ \begin{align} Y=M(X,Z) \end{align} \]
- 质量调整后的劳动 \(X=EL\):\(E\) 为劳动生产效率,\(L\) 为常规度量的劳动力(如工作时间);
- 质量调整后的资本 \(Z=HK\):\(H\) 为资本生产效率,\(K\) 为常规度量的资本。
假设上述生产函数与一般生产函数 \(Y = F(L,K)\) 具有相同的特征(传送门:与一般生产函数的比较):
- \(M\) 对 \(X\)、\(M\) 对 \(Z\) 可微
- 一阶导数为正:\(M_X \gt 0\),\(M_Z \gt 0\)
- 二阶导数为负:\(M_ {XX} \lt 0\),\(M_ {ZZ} \lt 0\)
假设竞争性的要素市场达到均衡,资本的收入份额为 \(\beta =rK/Y = qZ/Y\)
\[ \begin{align} \beta = \frac {M_Z Z } Y \end{align} \]
其中,\(q\) 为质量调整后资本 \(Z\) 的边际资本报酬。将上式改为增长率的表达式,为:
\[ \begin{align} G(\beta) = G(M_Z) +G(Z) - G(Y) \end{align} \]
由于假定 \(M\) 是线性齐次的,因此(为什么能得到下面的关系?):
\[ \begin{align} \begin{cases} M_X X + M_Z Z = Y \\ M_ {XX} X +M_ {XZ} Z=0 \\ M_ {ZX} X+M_ {ZZ} Z=0 \end{cases} \end{align} \]
补充:
齐次生产函数是:若投入的全部生产要素增加(或减少)\(\lambda\) 倍,总产出就增加(或减少)\(\lambda ^n\) 倍,其中 \(\lambda \neq 0\)。
如果 \(n=1\),则为线性齐次生产函数。此时要素投入变化和产出变化程度相同,具有规模报酬不变的特点。柯布-道格拉斯生产函数是典型的线性生产函数。
因此,要素替代弹性可以写作(为什么能得到下面的关系?):
\[ \begin{align} \sigma = \frac {M_X M_Z / M_{XZ} } Y \end{align} \]
由于 \((1-\beta ) = \frac {M_X X} {Y}\),因此:
\[ \begin{align} G(M_Z) =\frac { M_{XZ} dX + M_{ZZ} dZ } {M_Z} = \frac {1-\beta } {\sigma } \cdot [G(X) - G(Z) ] \end{align} \]
同理可以计算出:
\[ \begin{align} G(Y) = (1-\beta )G(X) + \beta G(E) \end{align} \]
将上述 \(G(M_Z)\) 与 \(G(Y)\) 的计算结果代入 \(G(\beta)\) 的表达式,可得:
\[ \begin{aligned} G(\beta) & = G(M_Z) +G(Z) - G(Y) \\ & = (1-\beta ) \frac {\sigma -1 } {\sigma } \cdot [G(Z)-G(X) ] \\ & = (1-\beta ) \frac {\sigma -1 } {\sigma } \cdot \left \{ [G(K)+G(H) ] - [G(L) + G(E) ] \right \} \end{aligned} \]
上式为资本收入份额的增长率,决定了资本的收入份额。
第一阶段 \(OA \to OB\):生产函数 \(M\) 的要素替代弹性很大,即 \(\sigma \gt 1\),当 \(G(K)+G(H) \gt G(L) + G(E)\) 时,资本的收入份额 \(\beta\) 将会增加;
第二阶段 \(OB \to OC\),根据希克斯的定义:
当生产函数 \(M\) 的要素替代弹性比较小(\(\sigma \lt 1\))时:
- \(G(H) \gt G(E)\):资本节约型技术进步、劳动节约型技术进步
- \(G(H) \lt G(E)\):资本利用型技术进步、劳动节约型技术进步
当生产函数 \(M\) 的要素替代弹性比较大(\(\sigma \gt 1\))时:
- \(G(H) \gt G(E)\):资本节约型技术进步、劳动利用型技术进步
- \(G(H) \lt G(E)\):资本节约型技术进步、劳动利用型技术进步
(在第二阶段的技术种类判定上,原书有问题)

